「ブラジルの1匹の蝶の羽ばたきがテキサスで竜巻を引き起こす」なら竜巻の予測はできない。ブラジルのすべての蝶を観測することはできないからだ。これはバタフライ効果として知られる。1963年にMITの気象学者エドワード・ローレンツが発表したシミュレーションが元になっている。下画像の黒と赤のように、1億分の1の初期条件の差が、長期的な振る舞いを変えてしまう。
$$ローレンツ方程式$$
$$X,Y,Z:何かしらの変数、t:時間$$
$$\frac{dX}{dt}=-10X+10Y$$
$$\frac{dY}{dt}=28X-XY-Y$$
$$\frac{dZ}{dt}=XY-\frac{8}{3}Z$$
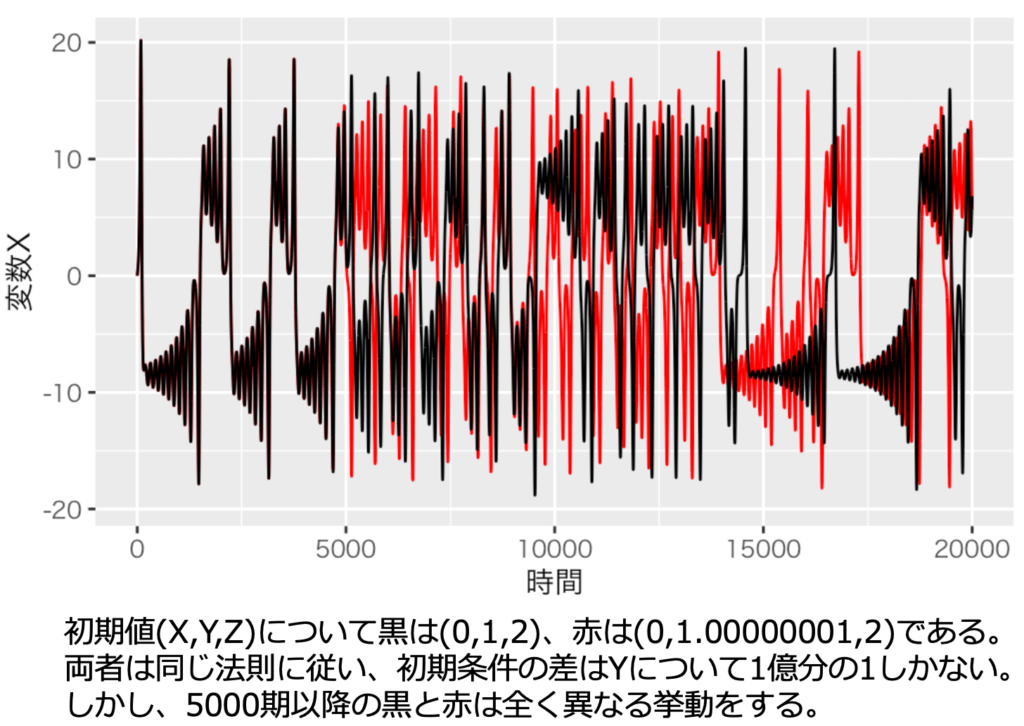
すべての物理法則が解明されても予測できないことはある。カオスだ。カオスとは、初期値鋭敏性を持つ決定論的現象だ。つまり、カオスは、ほんの少しの初期値の差異が長期的な振る舞いを完全に変えてしまう初期値鋭敏性を持つが、t期の状態が決まればt+1期の状態が決まる決定論的現象である。完璧で寸分の誤差のない観測は不可能であるがゆえに、カオスは予測不可能だ。さきほどのローレンツ・カオスがその代表例である。
運命が決まっていても予測できないなら、個々の人間にとって運命は存在しないに等しい。因果関係が複雑な社会では何が起こるかわからない。せいぜい確率でお茶を濁すしかないのである。
【付】
バタフライ効果の語源は、ローレンツが1972年に行った「ブラジルの一匹の蝶の羽ばたきはテキサスで竜巻を引き起こすか?」という講演のタイトルに由来する。
バタフライ効果については次の動画がとても面白い。
Rによるシミュレーションのコードを残しておく。
library(ggplot2)
a <- 10
b <- 28
c <- 8/3
T <- 30000
#モデル1の初期値
X0_1 <- 0
Y0_1 <- 1
Z0_1 <- 2
#モデル2の初期値
X0_2 <- 0
Y0_2 <- 1.00000001
Z0_2 <- 2
#モデル1の行列
data0<- data.frame(matrix(0,T,7))
colnames(data0) <- c("time","X1","Y1","Z1","X2","Y2","Z2")
data0[1,"X1"] <- X0_1
data0[1,"Y1"] <- Y0_1
data0[1,"Z1"] <- Z0_1
data0[1,"X2"] <- X0_2
data0[1,"Y2"] <- Y0_2
data0[1,"Z2"] <- Z0_2
#シミュレーション
for(t in 1:(T-1) ){
time <- data0[t, "time"]
X1 <- data0[t,"X1"]
Y1 <- data0[t,"Y1"]
Z1 <- data0[t,"Z1"]
X2 <- data0[t,"X2"]
Y2 <- data0[t,"Y2"]
Z2 <- data0[t,"Z2"]
data0[t+1,"time"] <- time + 1
data0[t+1,"X1"] <- X1 + (-1*a*X1+a*Y1)/200
data0[t+1,"Y1"] <- Y1 + (b*X1-X1*Z1-Y1)/200
data0[t+1,"Z1"] <- Z1 + (X1*Y1 - c*Z1)/200
data0[t+1,"X2"] <- X2 + (-1*a*X2+a*Y2)/200
data0[t+1,"Y2"] <- Y2 + (b*X2-X2*Z2-Y2)/200
data0[t+1,"Z2"] <- Z2 + (X2*Y2 - c*Z2)/200
}
ggplot(data0)+
geom_line(aes(x = time, y = X2),col="red")+
geom_line(aes(x = time, y = X1),col="black")+
xlab("時間") +
ylab ("変数X") +
scale_x_continuous(limits = c(0, 5000))+ #予測する期間を0から5000
ggtitle ("ローレンツ・カオス 黒が現実 赤が予測") +
theme_grey(base_family = "HiraKakuPro-W3")
#別解:モデル1のXの時系列プロット
matplot(1:(T-1),data0[1:(T-1), c("X1")], type="l",col=1,lwd = 2)