最適成長モデルでは、経済成長は鞍点経路(あんてんけいろ、サドル・パス、saddle path)に沿って実現し、最終的に定常均衡に到達する。これは大域的に安定である。つまり、一人当たり資本kが初期状態として与えられれば、消費者が最適な初期消費を決定し、あとは鞍点経路をたどって、定常均衡に到達する。
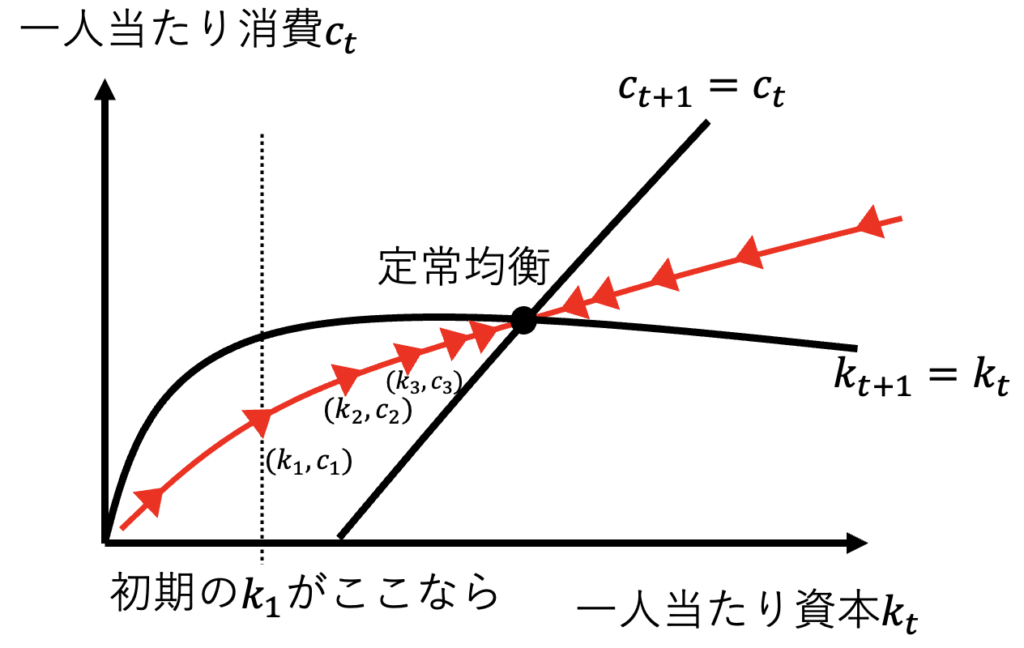
ところで、鞍点経路(サドル・パス)から外れるとどうなるのだろうか。考え方は二つある。第一は、鞍点経路から外れても新しく初期値の計算を実行できる場合である。その時の資本kにおける鞍点経路に戻るだけである。大域的な安定性は毀損されない。第二は、新しく初期値の計算を実行できない場合である。さらに、鞍点経路で成立する「t期が決まれば、t+1期が決まる」のルール(資本蓄積の動学方程式、オイラー方程式)に従うならば、最終的に不適切な経済が実現する。具体的には、「資本がゼロになり、消費がゼロになる」か「すべての生産が投資され、消費ゼロになる」かのどちらかの不適切な状態が実現する。ただし、これは消費者の効用最大化に違反しているので、実際は選ばれることはない。まとめると、鞍点経路から外れると、その時点の資本kにおける鞍点経路に戻るのである。
最適成長モデルは、市場メカニズムが働いた結果、最終的に定常均衡に到達するので、長期的には魯ソー・モデルと同じ結果となる。すなわち、技術進歩が一人当たりGDP(=生活水準)の成長率を決め、技術進歩と人口成長が国全体のGDP(=国力)の成長率を決める。
【追記:鞍点(あんてん、saddle point)】
鞍点は「多変数実関数の変域の中で、ある方向で見れば極大値だが別の方向で見れば極小値となる点」である。2変数関数の例では、次のようなものが挙げられる。
$$(X,Y)=(\bar{x},\bar{y})がF(X,Y)について鞍点とは$$
$$例えば、F(\bar{x},\bar{y})がxについての極大値、yについての極小値。$$
【追記:問題】
鞍点経路(サドル・パス)についての分析を簡単にするために、人口成長率と技術進歩率がゼロとする。そして、技術係数=1、人口=1とする。そして、マクロ生産関数は次のように設定する。
$$F(K_t,A_t L_t)=F(K_t,1)=f(k_t)$$
$$ただし、k_tは一人当たり資本$$
問1(企業・動学):次の資本遷移式を一人当たりに直し、左辺にc_tが来る形にせよ。なお、集計変数は大文字、一人当たりの変数は小文字で表記する。
$$K_{t+1}=K_t+I_t-\delta K_t$$
問2(企業・一定):一人当たりの資本が一定になる条件を導け。それを縦軸がc、横軸がkのグラフとせよ。
問3(消費者・動学):オイラー方程式を求めよ。一人当たりの所得で制約される中で、一人当たりの消費量C/Lから得られる生涯効用を最大化していると考えよ。答えのオイラー方程式に含まれる効用関数はu(c)でよい。また、利子率rは、企業が利潤最大化していることを用いて処理せよ。
問4(消費者・一定):一人当たり消費cが一定となる条件を求めよ。一人当たり消費cが一定となる条件を縦軸がc、横軸がkのグラフとすると、直線ではなく曲線になることを示せ。
問5(定常均衡):資本と消費の動学モデルを立てよ。時間が進んでも一人当たり消費や一人当たり資本が変化しない定常均衡を表す連立方程式を立てよ。
問6(数式・まとめ):次のマクロ生産関数と効用関数を仮定して、動学モデル、資本、消費一定の曲線、定常均衡を求めよ。ただし、A=L=1である。
問7(位相図):t+1期の一人当たりの資本が増えるのは、問2のグラフのどの領域か?
問8(位相図):t+1期の一人当たりの消費が増えるのは、問4のグラフのどの領域か?
問9(位相図):問7と問8の結果を用いて、定常均衡に到達する可能性のある領域を示せ。
問10(R・プログラミング):問6の結果と以下のパラメーターを用いて、R言語にてラムゼイ・モデルを作図せよ。具体的には、資本一定、消費一定の曲線を図示せよ。次の初期値からはじまる経路を図示せよ。シミュレーション期間はT=50期。
・α=0.3、β= 0.99、δ=0.25
・初期値(k1,c1)=(0.5, 0.5116194408)
問11(R・プログラミング):定常均衡にいたる鞍点経路(サドル・パス)は一つしかない。効用最大化とポンジゲーム禁止条件のために、一人当たり資本kを選べば、最適な一人当たり消費c(=鞍点経路にあるc)が選ばれる。しかし、最適ではないcを選んで、さらに鞍点経路で成立する動学モデルを繰り返し用いると、プラスの消費とプラスの資本の定常均衡に至ることができない。それを問10のプログラムを持ちて、図示せよ。
・初期値(k1,c1)=(0.5, 0.5116194408),(0.5,0.5),(0.5,0.5116194408),(0.5,0.52),(7,1.85),(7,1.90027826),(7,2)
問12(Dynara・プログラミング):MatlabのDynareを用いて、鞍点経路(サドル・パス)を図示せよ。
【追記:問題】
鞍点経路(サドル・パス)についての分析を簡単にするために、人口成長率と技術進歩率がゼロとする。そして、技術係数=1、人口=1とする。そして、マクロ生産関数は次のように設定する。
$$F(K_t,A_t L_t)=F(K_t,1)=f(k_t)$$
$$ただし、k_tは一人当たり資本$$
問1:次の資本遷移式を一人当たりに直し、左辺にc_tが来る形にせよ。なお、集計変数は大文字、一人当たりの変数は小文字で表記する。
$$K_{t+1}=K_t+I_t-\delta K_t$$
$$K_{t+1}=(1- \delta )K_t+(Y_t-C_t)$$
$$K_{t+1}=(1- \delta )K_t+F(K_t,A_t L_t)-C_t$$
$$k_{t+1}=(1- \delta )k_t+f(k_t)-c_t・・・式1$$
$$これを資本蓄積の動学方程式という。$$
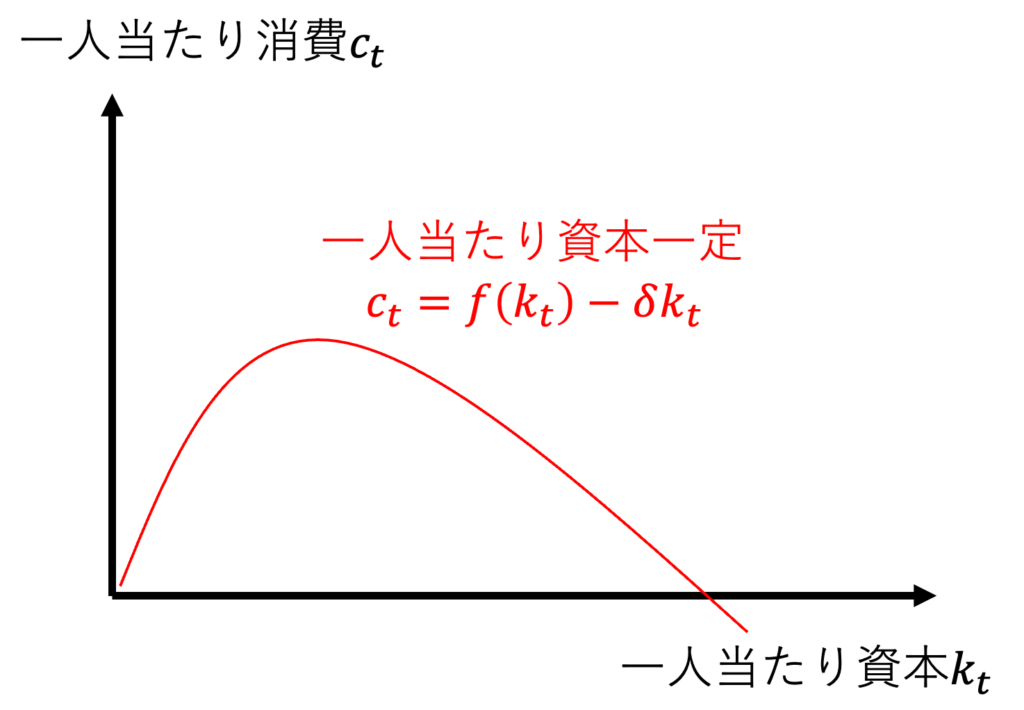
問2:一人当たりの資本が一定になる条件を導け。それを縦軸がc、横軸がkのグラフとせよ。
$$一人当たりの資本一定k_t=k_{t+1}を式1に代入して$$
$$k_t=(1- \delta )k_t+f(k_t)-c_t$$
$$c_t=f(k_t)-\delta k_t$$
$$要は、一人当たりの資本一定k_t=k_{t+1}になるには$$
$$消費=生産量-資本減耗を埋め合わせるのに必要な投資$$
$$が必要とのことであり、直感的な結果だ。$$
$$グラフを描こう。$$
問3:オイラー方程式を求めよ。一人当たりの所得で制約される中で、一人当たりの消費量C/Lから得られる生涯効用を最大化していると考えよ。答えのオイラー方程式に含まれる効用関数はu(c)でよい。また、利子率rは、企業が利潤最大化していることを用いて処理せよ。
$$\max \sum_{t=0}^{\infty} \beta^t u \left( \frac{C_t}{L_t} \right)$$
$$s.t. \frac{C_t}{L_t}+\frac{[Asset]_t}{L_t}=(1+r_t)\frac{[Asset]_{t-1}}{L_t}+\frac{w_t L_t}{L_t}$$
$$ただし人口が1なので、一人当たりを小文字にして$$
$$\max \sum_{t=0}^{\infty} \beta^t u ( c_t)$$
$$s.t. c_t+[asset]_t=(1+r_t)[Asset]_{t-1}+w_t$$
$$ここでラグランジュの未定乗数法を用いる。$$
$$L=\sum_{t=0}^{\infty} \beta^t u (c_t)+\sum_{t=0}^{\infty} \lambda_t \left( (1+r_t)[asset]_{t-1} +w_t – c_t-[asset]_t \right) $$
$$ラグランジュ関数をc_tと[asset]_tで微分すればゼロなので$$
$$\frac{\partial L}{\partial c_t}=\beta^t u'(c_t) -\lambda_t =0・・・式2$$
$$\frac{\partial L}{\partial [asset]_t }=\lambda_{t+1} (1+r_{t+1})-\lambda_{t} =0・・・式3$$
$$式2と式3より、u'(c_t)=\beta (1+ r_{t+1})u'(c_{t+1})・・・式4$$
$$利潤最大化条件 r_{t+1}=f'(k_{t+1})-\deltaを式4に代入して$$
$$\frac{u'(c_t)}{u'(c_{t+1})}=\beta (1+ f'(k_{t+1})-\delta)$$
$$これが消費の動学に関するオイラー方程式ある。$$
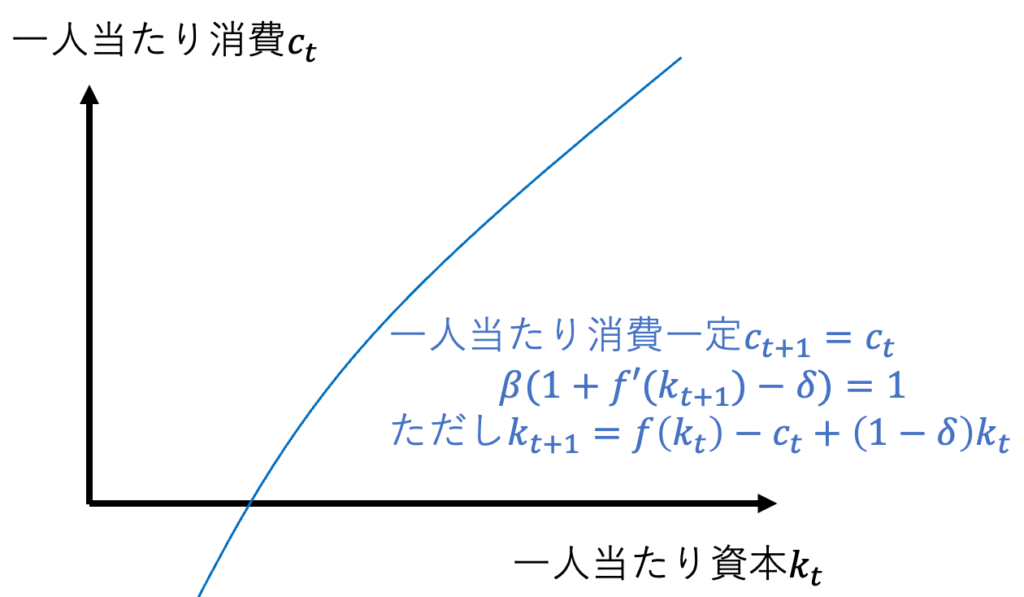
問4:一人当たり消費cが一定となる条件を求めよ。一人当たり消費cが一定となる条件を縦軸がc、横軸がkのグラフとすると、直線ではなく曲線になることを示せ。
$$一人当たりの消費一定c_t=c_{t+1}より$$
$$1=\beta (1+ f'(k_{t+1})-\delta)$$
$$ f'(k_{t+1})=\frac{1+\beta + \beta \delta}{\beta}$$
$$したがって、一人当たり消費c_t=c_{t+1}が一定となるならば$$
$$次の期の資本の限界生産性f'(k_{t+1})が一定である必要があり、$$
$$一人当たりk_{t+1}も一定である必要がある。$$
$$k_{t+1}=f(k_t)+(1-\delta) k_t-c_t↑とc_tが増えてもk_{t+1}が一定になるには$$
$$c_tが増えた分、k_tが増える必要がある。$$
$$一人当たり消費cが一定となる条件を図示すると、右上がりの軌跡となる。$$
$$要は、高い生活水準を恒常的に実現するには$$
$$一人当たり資本を増やさなければならない。直感的にも正しい。$$
$$グラフにすると次のようになる。$$
問5:資本と消費の動学モデルを立てよ。時間が進んでも一人当たり消費や一人当たり資本が変化しない定常均衡を表す連立方程式を立てよ。
$$資本蓄積の動学方程式:k_{t+1}=(1- \delta )k_t+f(k_t)-c_t$$
$$オイラー方程式:\frac{u'(c_t)}{u'(c_{t+1})}=\beta (1+ f'(k_{t+1})-\delta)$$
$$定常均衡(k^*,c^*)について$$
$$資本一定よりc^*=f(k^*)-\delta k^*$$
$$次に消費一定であるが、縦軸がk_t、横軸がc_tであることに注目してほしい。$$
$$消費一定の式にあるのはt+1のkである。$$
$$\beta (1+ f'(k_{t+1})-\delta)=1なので$$
$$1=\beta \left( 1+ \frac{ \partial[f((1- \delta )k_t+f(k_t)-c_t)]}{\partial k_{t+1}}-\delta \right)$$
問6:次のマクロ生産関数と効用関数を仮定して、動学モデル、資本、消費一定の曲線、定常均衡を求めよ。ただし、A=L=1である。
$$F(K_t,A_t L_t)=K_t^{\alpha}(A_t L_t)^{1-\alpha}$$
$$u \left( \frac{C_t}{L_t} \right)=\log \left( \frac{C_t}{L_t} \right)$$
$$A=L=1より、f(k_t)=k_t^{\alpha}、u(c_t)=\log c_t$$
$$【動学モデル】$$
$$k_{t+1}=(1- \delta )k_t+k_t^{\alpha}-c_t$$
$$c_{t+1}=c_t\beta (1+ f'(k_{t+1})-\delta)$$
$$=c_t\beta (1+ \alpha k_{t+1}^{\alpha-1}-\delta)$$
$$=c_t \beta \left(1+ \alpha \left( \alpha k_t^{\alpha -1}+(1-\delta) k_t-c_t \right) ^{\alpha-1}-\delta \right)$$
$$【資本、消費一定の曲線】$$
$$資本一定:c=k^{\alpha}-\delta k$$
$$消費一定:\beta (1+ \alpha k_{t+1}^{\alpha-1}-\delta)=1$$
$$\beta (1+ \alpha ((1- \delta )k_t+k_t^{\alpha}-c_t)^{\alpha-1}-\delta)=1$$
$$c_t=k_t^{\alpha}+( 1-\delta)k_t- \left( \frac{1}{\alpha \beta}+\frac{\delta}{\alpha}-\frac{1}{\alpha} \right) ^\frac{1}{\alpha-1}$$
$$【定常均衡】$$
$$ k=\left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{1}{\alpha – 1}}$$
$$c =\left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{\alpha}{\alpha – 1}}-\delta \left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{1}{\alpha – 1}}$$
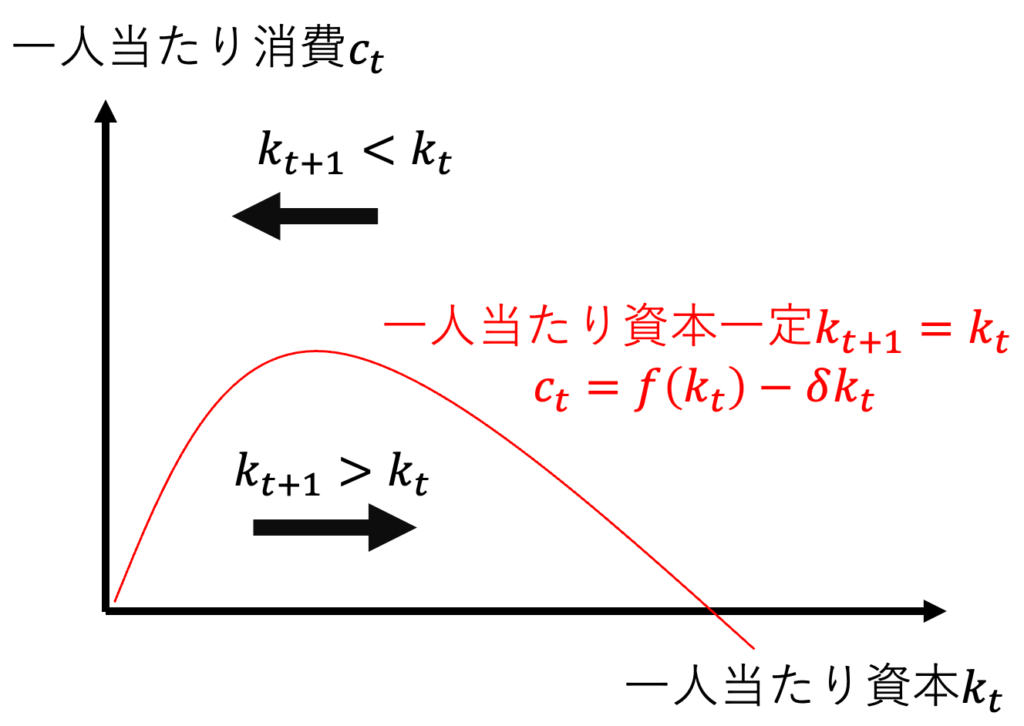
問7:t+1期の一人当たりの資本が増えるのは、問2のグラフのどの領域か?
$$赤い曲線上の資本一定となる点を(k_t^*,c_t^*)とする。$$
$$資本の動学方程式の(k_t,c_t)に(k_t^*,c_t^*)を代入すると$$
$$k_{t+1}=(1- \delta )k_t^*+f(k_t^*)-c_t^*=k_{t}^*$$
$$次に、資本の動学方程式の(k_t,c_t)に(k_t^*,c_t^*-\Delta)を代入すると(\Delta>0)$$
$$k_{t+1}=(1- \delta )k_t^*+f(k_t^*)-(c_t^*-\Delta)=k_{t}^*+\Delta$$
$$したがって、t期に(k_{t},c_{t})=(k_t^*,c_t^*-\Delta)であれば$$
$$t+1期に(k_{t+1},c_{t+1})=(k_{t}^*+\Delta,?)となる。$$
$$なぜなら、資本減耗以上の投資が実現し、資本が増加するからだ。$$
$$(k_t^*,c_t^*-\Delta)は資本一定となる赤い曲線(k_t^*,c_t^*)の下の領域である。$$
$$グラフにすると、次のように表現できる。$$
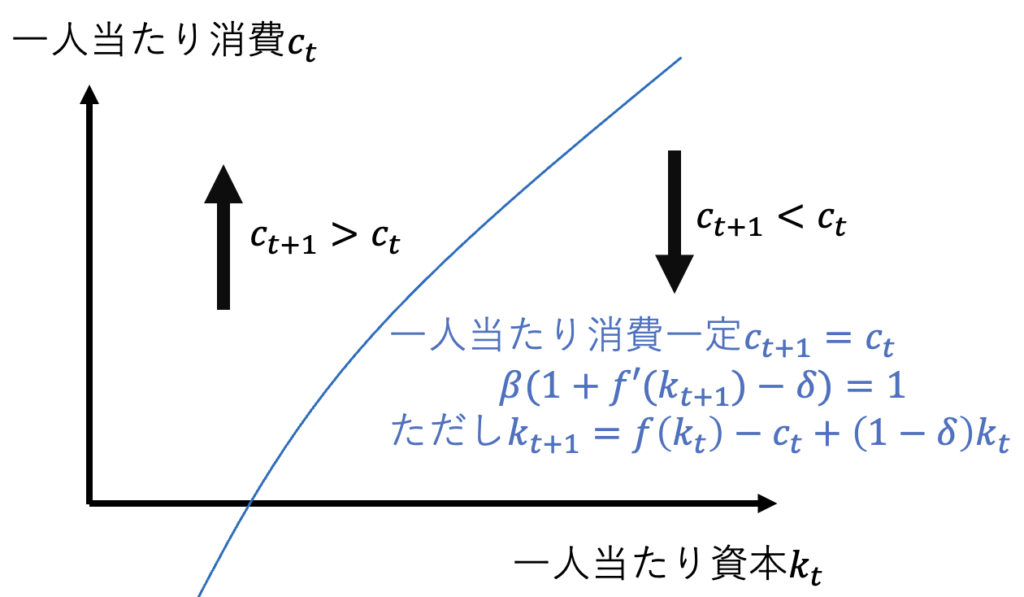
問8:t+1期の一人当たりの消費が増えるのは、問4のグラフのどの領域か?
$$青い軌跡上の消費一定となる点を(k_t^*,c_t^*)とする。$$
$$オイラー方程式\frac{u'(c_t)}{u'(c_{t+1})}=\beta (1+ f'(k_{t+1})-\delta)に$$
$$(k_t,c_t)=(k_t^*,c_t^*)を代入すると$$
$$\frac{u'(c_t^*)}{u'(c_{t+1})}=\beta (1+ f'(k_{t+1})-\delta)=1$$
$$ただしk_{t+1}=(1- \delta )k_t^*+f(k_t^*)-c_t^*$$
$$次に、オイラー方程式の(k_t,c_t)に(k_t^*-\Delta,c_t^*)を代入すると(\Delta>0)$$
$$k_{t+1}↓=(1- \delta )(k_t^*-\Delta)+f(k_t^*-\Delta)-c_t^*となる。$$
$$したがってf'(k_{t+1}↓)↑であり$$
$$\frac{u'(c_t^*)}{u'(c_{t+1})}=\beta (1+ f'(k_{t+1})↑-\delta)>1$$
$$u'(c_t^*)>u'(c_{t+1})は限界効用逓減よりc_t^*<c_{t+1}を意味する。$$
$$したがって、t期に(k_{t},c_{t})=(k_t^*-\Delta,c_t^*)であれば$$
$$t+1期に(k_{t+1},c_{t+1})=(?,c_t^*↑)となる。$$
$$なぜなら、一人当たり資本が低水準で旺盛な投資需要のために$$
$$利子率が高く、資本所得が高いので、t+1期の消費が増える。$$
$$(k_t^*-\Delta,c_t^*)は資本一定となる赤い曲線(k_t^*,c_t^*)の左の領域である。$$
$$グラフにすると、次のように表現できる。$$
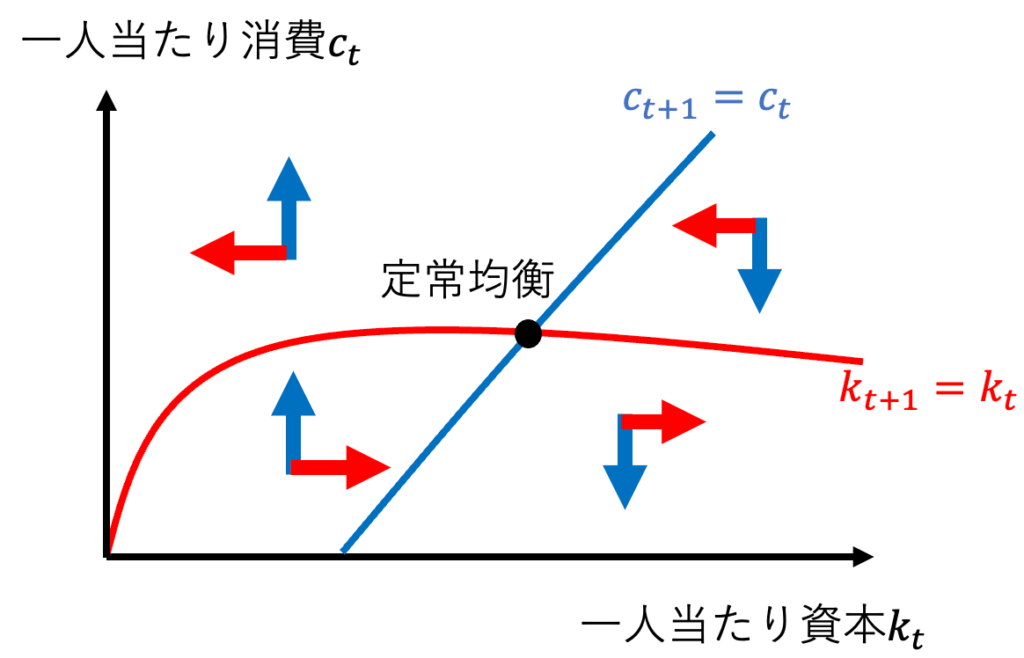
問9:問7と問8の結果を用いて、定常均衡に到達する可能性のある領域を示せ。
下図の左下と右下が定常均衡に到達する可能性がある。
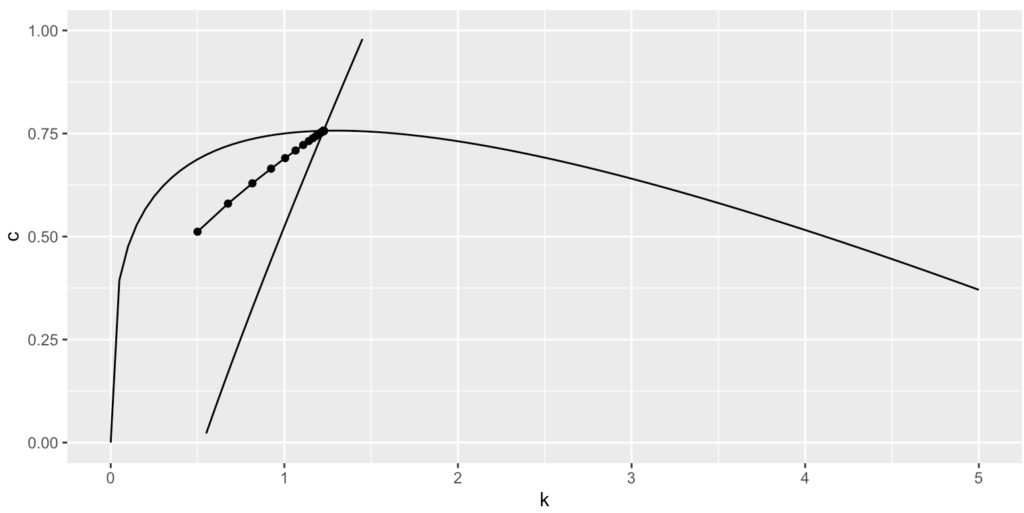
問10:問6の結果と以下のパラメーターを用いて、R言語にてラムゼイ・モデルを作図せよ。具体的には、資本一定、消費一定の曲線を図示せよ。次の初期値からはじまる経路を図示せよ。シミュレーション期間はT=50期。
・α=0.3、β= 0.99、δ=0.25
・初期値(k1,c1)=(0.5, 0.5116194408)
$$【資本、消費一定の曲線】$$
$$資本一定:c=k^{\alpha}-\delta k$$
$$消費一定:c_t=k_t^{\alpha}+( 1-\delta)k_t- \left( \frac{1}{\alpha \beta}+\frac{\delta}{\alpha}-\frac{1}{\alpha} \right) ^\frac{1}{\alpha-1}$$
$$【動学モデル】$$
$$k_{t+1}=(1- \delta )k_t+k_t^{\alpha}-c_t$$
$$c_{t+1}=c_t\beta (1+ \alpha k_{t+1}^{\alpha-1}-\delta)$$
$$【定常均衡】$$
$$ k=\left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{1}{\alpha – 1}}$$
$$c =\left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{\alpha}{\alpha – 1}}-\delta \left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{1}{\alpha – 1}}$$
#変数説明
#k=一人当たり資本、c=一人当たり消費
#行列準備
T <- 50 #シミュレーション期間
Data<- data.frame(matrix(0,T,3))
colnames(Data) <- c("time","k","c")
#初期値
Data[1,"time"] <- 1
Data[1,"k"] <- 0.5
Data[1,"c"] <- 0.5116194408
#パラメーター
a <- 0.3 #資本分配率α
b <- 0.99 #割引因子β
d <- 0.25 #資本減耗率δ
#資本蓄積の動学方程式
k_dynamicK <- function(k,c,a,d) {
nextK <- (1-d)*k +k^a -c
realNextK <- ifelse(nextK> 0,nextK, 0)
return(realNextK)
}
#オイラー方程式
c_dynamicK <- function(nextK,c,a,b,d) {
nextC <- c*b*(1+a*nextK^(a-1)-d)
realNextC <- ifelse(nextK > 0,nextC, c + (nextC-c)*((k)/(k-nextK)))
return(realNextC)
}
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1)){
Data[t+1,"time"] <- 1 + Data[t,"time"]
k <- Data[t,"k"]
c <- Data[t,"c"]
nextK <- k_dynamicK(k,c,a,d)
nextC <- c_dynamicK(nextK,c,a,b,d)
Data[t+1,"k"] <- nextK
Data[t+1,"c"] <- nextC
}
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#消費一定の消費
c_constantC <- function(k,a,b,d) {
A <- (1/(a*b)) + (d/a) -(1/a)
c <- k^a + (1-d)*k - A^(1/(a-1))
return(c)
}
c_constantC_graph<- function(k) {
c <- c_constantC(k,a,b,d)
return(c)
}
#資本一定の消費
c_constantK <- function(k,a,d) {
c <- k^a - d*k
return(c)
}
c_constantK_graph<- function(k) {
c <- c_constantK(k,a,d)
return(c)
}
ggplot()+
geom_path(data=Data,aes(x = k, y = c))+
geom_point(data=Data,aes(x = k, y = c))+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X),fun = c_constantC_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X),fun = c_constantK_graph)+
scale_x_continuous(limits=c(0,5))+
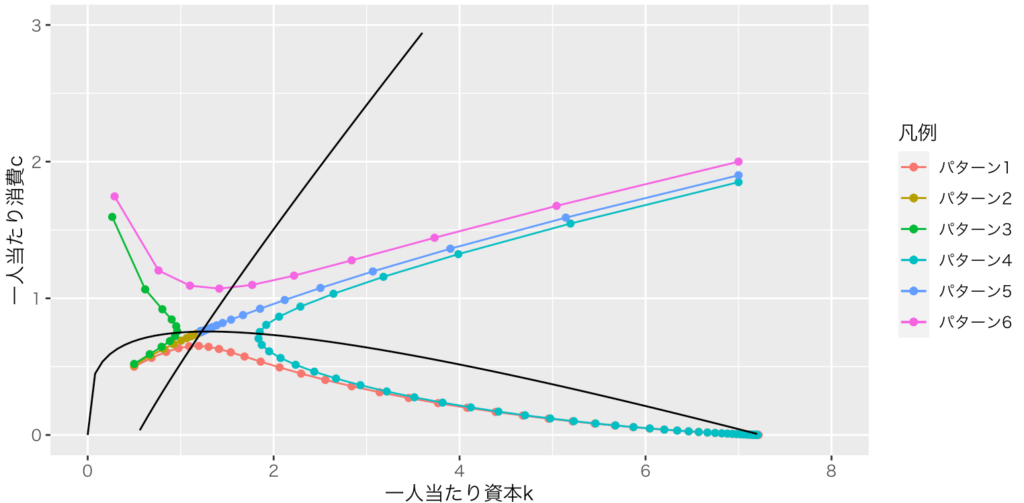
scale_y_continuous(limits=c(0,1))問11:定常均衡にいたる鞍点経路(サドル・パス)は一つしかない。効用最大化とポンジゲーム禁止条件のために、一人当たり資本kを選べば、最適な一人当たり消費c(=鞍点経路にあるc)が選ばれる。しかし、最適ではないcを選んで、さらに鞍点経路で成立する動学モデルを繰り返し用いると、プラスの消費とプラスの資本の定常均衡に至ることができない。それを問10のプログラムを持ちて、図示せよ。
・初期値(k1,c1)=(0.5, 0.5116194408),(0.5,0.5),(0.5,0.5116194408),(0.5,0.52),(7,1.85),(7,1.90027826),(7,2)

#変数説明
#k=一人当たり資本、c=一人当たり消費
#行列準備
T <- 50 #シミュレーション期間
Data<- data.frame(matrix(0,T,7))
colnames(Data) <- c("time","k1","c1","k2","c2","k3","c3","k4","c4","k5","c5","k6","c6")
#初期値
Data[1,"time"] <- 1
Data[1,"k1"] <- 0.5 #パターン1:kマイナスへ到達
Data[1,"c1"] <- 0.5 #パターン1:kマイナスへ到達
Data[1,"k2"] <- 0.5 #パターン2:定常均衡へ
Data[1,"c2"] <- 0.5116194408 #パターン2:定常均衡へ
Data[1,"k3"] <- 0.5 #パターン3:c=0に収束
Data[1,"c3"] <- 0.52 #パターン3:c=0に収束
Data[1,"k4"] <- 7 #パターン4:U字を描いてc=0に収束
Data[1,"c4"] <- 1.85 #パターン4:U字を描いてc=0に収束
Data[1,"k5"] <- 7 #パターン5:定常均衡へ
Data[1,"c5"] <- 1.90027826 #パターン5:定常均衡へここお
Data[1,"k6"] <- 7 #パターン6:kマイナスへ到達
Data[1,"c6"] <- 2 #パターン6:kマイナスへ到達
#パラメーター
a <- 0.3 #資本分配率α
b <- 0.99 #割引因子β
d <- 0.25 #資本減耗率δ
#資本蓄積の動学方程式
k_dynamicK <- function(k,c,a,d) {
nextK <- (1-d)*k +k^a -c
return(nextK)
}
#オイラー方程式
c_dynamicK <- function(nextK,c,a,b,d) {
nextC <- c*b*(1+a*nextK^(a-1)-d)
return(nextC)
}
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1)){
#時間カウント
Data[t+1,"time"] <- 1 + Data[t,"time"]
#シミュレーション1
k1 <- Data[t,"k1"]
c1 <- Data[t,"c1"]
nextK1 <- k_dynamicK(k1,c1,a,d)
nextC1 <- c_dynamicK(nextK1,c1,a,b,d)
Data[t+1,"k1"] <- nextK1
Data[t+1,"c1"] <- nextC1
#シミュレーション2
k2 <- Data[t,"k2"]
c2 <- Data[t,"c2"]
nextK2 <- k_dynamicK(k2,c2,a,d)
nextC2 <- c_dynamicK(nextK2,c2,a,b,d)
Data[t+1,"k2"] <- nextK2
Data[t+1,"c2"] <- nextC2
#シミュレーション3
k3 <- Data[t,"k3"]
c3 <- Data[t,"c3"]
nextK3 <- k_dynamicK(k3,c3,a,d)
nextC3 <- c_dynamicK(nextK3,c3,a,b,d)
Data[t+1,"k3"] <- nextK3
Data[t+1,"c3"] <- nextC3
#シミュレーション4
k4 <- Data[t,"k4"]
c4 <- Data[t,"c4"]
nextK4 <- k_dynamicK(k4,c4,a,d)
nextC4 <- c_dynamicK(nextK4,c4,a,b,d)
Data[t+1,"k4"] <- nextK4
Data[t+1,"c4"] <- nextC4
#シミュレーション5
k5 <- Data[t,"k5"]
c5 <- Data[t,"c5"]
nextK5 <- k_dynamicK(k5,c5,a,d)
nextC5 <- c_dynamicK(nextK5,c5,a,b,d)
Data[t+1,"k5"] <- nextK5
Data[t+1,"c5"] <- nextC5
#シミュレーション6
k6 <- Data[t,"k6"]
c6 <- Data[t,"c6"]
nextK6 <- k_dynamicK(k6,c6,a,d)
nextC6 <- c_dynamicK(nextK6,c6,a,b,d)
Data[t+1,"k6"] <- nextK6
Data[t+1,"c6"] <- nextC6
}
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#消費一定グラフ描画用の関数
c_constantC <- function(k,a,b,d) {
A <- (1/(a*b)) + (d/a) -(1/a)
c <- k^a + (1-d)*k - A^(1/(a-1))
return(c)
}
c_constantC_graph<- function(k) {
c <- c_constantC(k,a,b,d)
return(c)
}
#資本一定グラフ描画用の関数
c_constantK <- function(k,a,d) {
c <- k^a - d*k
return(c)
}
c_constantK_graph<- function(k) {
c <- c_constantK(k,a,d)
return(c)
}
#描画
ggplot()+
geom_path(data=Data,aes(x = k1, y = c1,colour = "パターン1"))+
geom_point(data=Data,aes(x = k1, y = c1,colour = "パターン1"))+
geom_path(data=Data,aes(x = k2, y = c2,colour = "パターン2"))+
geom_point(data=Data,aes(x = k2, y = c2,colour = "パターン2"))+
geom_path(data=Data,aes(x = k3, y = c3,colour = "パターン3"))+
geom_point(data=Data,aes(x = k3, y = c3,colour = "パターン3"))+
geom_path(data=Data,aes(x = k4, y = c4,colour = "パターン4"))+
geom_point(data=Data,aes(x = k4, y = c4,colour = "パターン4"))+
geom_path(data=Data,aes(x = k5, y = c5,colour = "パターン5"))+
geom_point(data=Data,aes(x = k5, y = c5,colour = "パターン5"))+
geom_path(data=Data,aes(x = k6, y = c6,colour = "パターン6"))+
geom_point(data=Data,aes(x = k6, y = c6,colour = "パターン6"))+
stat_function(data=data.frame(X=c(0,4)), aes(x=X),fun = c_constantC_graph)+
stat_function(data=data.frame(X=c(0,4)), aes(x=X),fun = c_constantK_graph)+
scale_x_continuous(limits=c(0,8))+
scale_y_continuous(limits=c(0,3))+
labs(color = "凡例")+
xlab("一人当たり資本k") +
ylab ("一人当たり消費c") +
theme_grey(base_family = "HiraKakuPro-W3")問12:MatlabのDynareを用いて、鞍点経路(サドル・パス)を図示せよ。
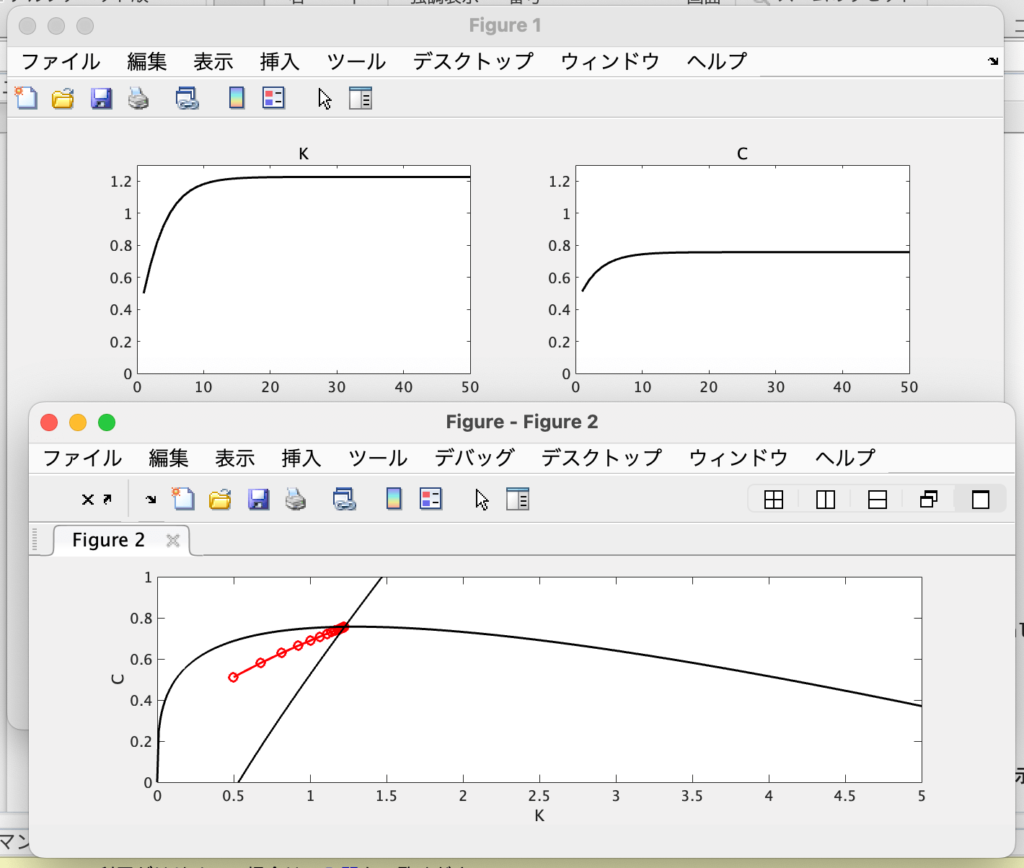
日本語あり、解説版。
// ラムゼイモデル
// 変数
var K C; // 変数名を宣言
// 定数
// 定数>パラメーター
parameters alpha beta delta; // パラメーター名を宣言
alpha = 0.3; // α=0.3とする
beta = 0.99;
delta = 0.25;
// モデル
// モデル>動学モデル(これは自分で計算しないといけない)
model;
0 = C(+1)/C - beta*(1 + alpha*K^(alpha-1) - delta );//オイラー方程式
0 = K - (K(-1)^alpha + (1-delta)*K(-1) - C); // 資本蓄積の動学方程式
end;
// 初期値(これに近い初期値をプログラムが何度も試して、最終期にほぼ動かなくなる初期値を探す。)
initval;
K = 0.5;
C = 0.5;
end;
// シミュレーション
perfect_foresight_setup(periods=100); //完全予見で100期シミュレーション
perfect_foresight_solver; //シミュレーション実行
simu1 = oo_.endo_simul; //シミュレーション結果をデータセットsimu1に格納
//終点のT期
T=50;
//一枚目の図
//変数ごとのグラフ
figure(1);
// K
subplot(2,2,1)
plot([1:T],simu1(1,1:T),'k','LineWidth',1.5);
title('K')
xlim([0 T])
ylim([0 1.3])
// 解説
// subplot(縦方向に数えた図の個数,横方向に数えた図の個数,表示させたい場所を通し番号で記載)
// plot(横軸1~T期,縦軸simu1の1個の変数を1~t期,'色k=黒、r=赤',線の幅'LineWidth',←を1.5で指定);
// title('K') タイトルをKに
// xlim([0 T]) 横軸(x軸)の描画範囲を0からTへ。縦軸はylim
// C
subplot(2,2,2)
plot([1:T],simu1(2,2:T+1),'k','LineWidth',1.5);
title('C')
xlim([0 T])
ylim([0 1.3])
//二枚目の図
// Ktの範囲と粗さ
Kt = 0:0.01:10;
figure(2);
// シミュレーション描画
plot(simu1(1,1:T),simu1(2,2:T+1),'r','LineWidth',1.5);
// 解説
// plot(横軸の変数,縦の変数,'色k=黒、r=赤','LineWidth',線の幅);
// simu1(1,1:T) データセットsimu1の1個目の変数を1〜Tにかけて呼び出す
xlabel('K') // ラベル名
ylabel('C')
xlim([0 5]) // 軸範囲
ylim([0 1])
hold on // 次のものをfigure(2)に上塗り
// 資本一定のグラフ(これは自分で計算しないといけない)
// なお「.」をつけないと行列計算になってしまうので注意
plot(Kt,Kt.^alpha-delta*Kt,'k','LineWidth',1.5);
// 消費一定のグラフ(これは自分で計算しないといけない)
plot(Kt, Kt.^alpha + (1-delta).*Kt -(1./(alpha.*beta) +delta./alpha - 1./alpha).^(1./(alpha - 1)),'k','LineWidth',1.5);
//コマンドウィンドウで実行すべきコード
//dynare ファイル名.mod (modは省略可)
//装飾。上を実行した後で、表示>プロットブラウザー>赤い鞍点経路をクリック>マーカー>oで時間ごとの経路を表示できる。日本語なし。
var K C;
parameters alpha beta delta;
alpha = 0.3; // α=0.3とする
beta = 0.99;
delta = 0.25;
model;
0 = C(+1)/C - beta*(1 + alpha*K^(alpha-1) - delta );
0 = K - (K(-1)^alpha + (1-delta)*K(-1) - C);
end;
initval;
K = 0.5;
C = 0.5;
end;
perfect_foresight_setup(periods=100);
perfect_foresight_solver;
simu1 = oo_.endo_simul;
T=50;
figure(1);
subplot(2,2,1)
plot([1:T],simu1(1,1:T),'k','LineWidth',1.5);
title('K')
xlim([0 T])
ylim([0 1.3])
subplot(2,2,2)
plot([1:T],simu1(2,2:T+1),'k','LineWidth',1.5);
title('C')
xlim([0 T])
ylim([0 1.3])
Kt = 0:0.01:10;
figure(2);
plot(simu1(1,1:T),simu1(2,2:T+1),'r','LineWidth',1.5);
xlabel('K')
ylabel('C')
xlim([0 5])
ylim([0 1])
hold on
plot(Kt,Kt.^alpha-delta*Kt,'k','LineWidth',1.5);
plot(Kt, Kt.^alpha + (1-delta).*Kt -(1./(alpha.*beta) +delta./alpha - 1./alpha).^(1./(alpha - 1)),'k','LineWidth',1.5);