景気循環について / ソロー・モデル

2023.11.14

　ソロー・モデルに景気循環を組み込んでみよう。そのために、経済に確率的なショックを与える。そもそも、ソロー・モデルは、初期状態が決まれば全期間の変数が確定する決定論的モデルである。しかし、技術係数Aが確率的に変動するならば、確率論的モデルにソロー・モデルを書き換えられる。この記事では、3つの技術係数の変動を想定し、３つを比較した。恒久的なショックとは、t期のショックがそれ以降のt+1期にも影響を与えるショックである。一時的なショックとは、t期のショックがt+1期に影響を与えないショックである。

　

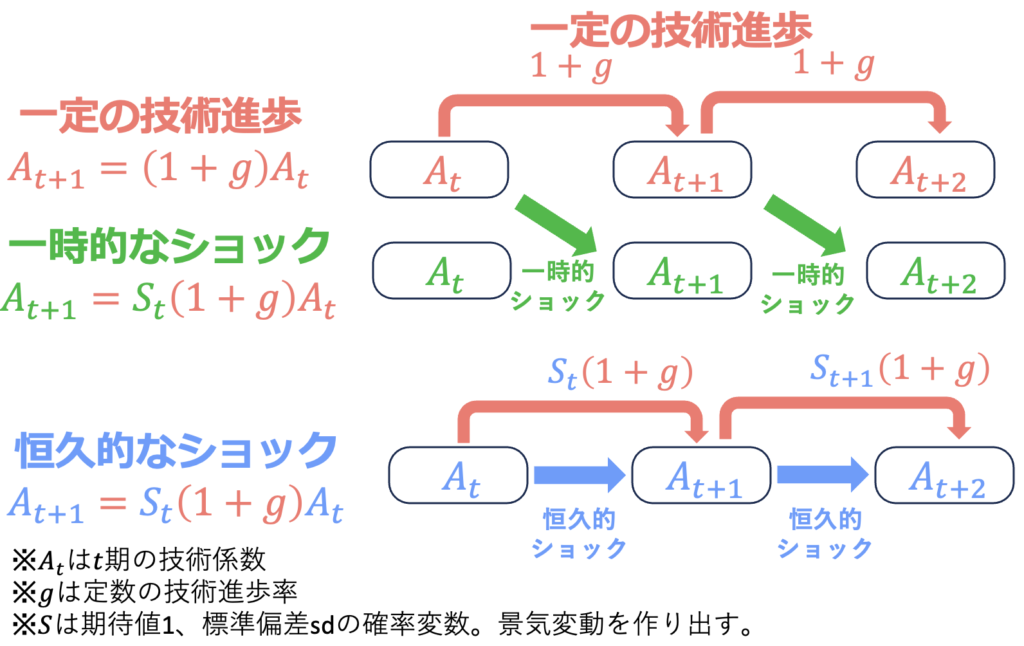
　技術進歩率gは0、標準偏差sdは0.05としてシミュレーションを行った。乱数を発生させるのでシミュレーションのたびに生成される結果は異なる。その結果例が次の画像1〜４である。一時的なショックが実現する経済は、ショックがない場合とほぼ同じである。しかし、永続的なショックがある経済は、時にショックがない場合と全く異なる経済状態を実現する。

画像１：水準効果なし
画像２：プラスの水準効果
画像３：マイナスの水準効果
画像４：景気循環

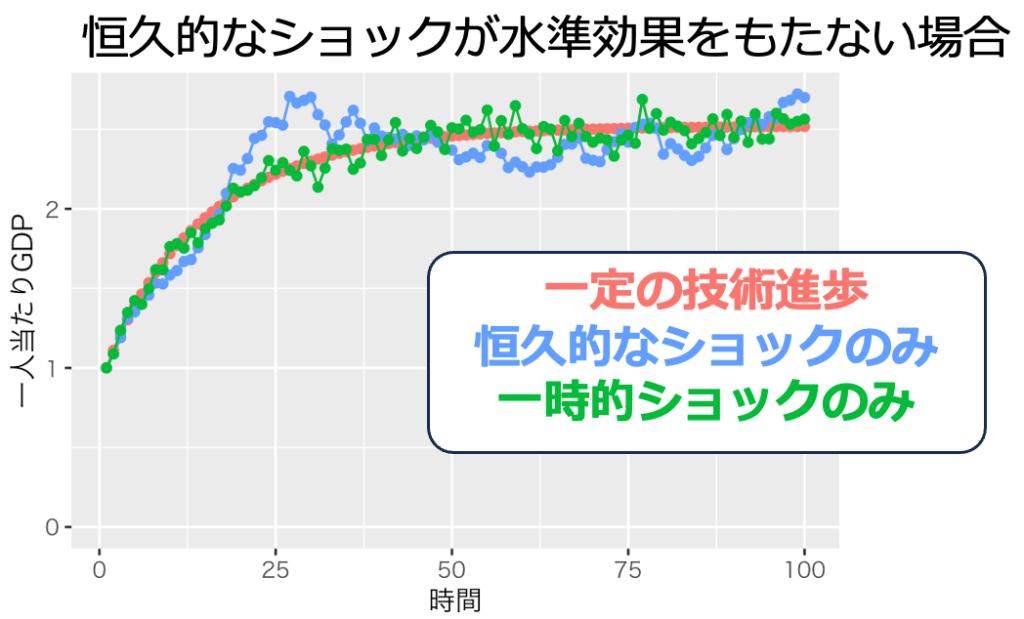
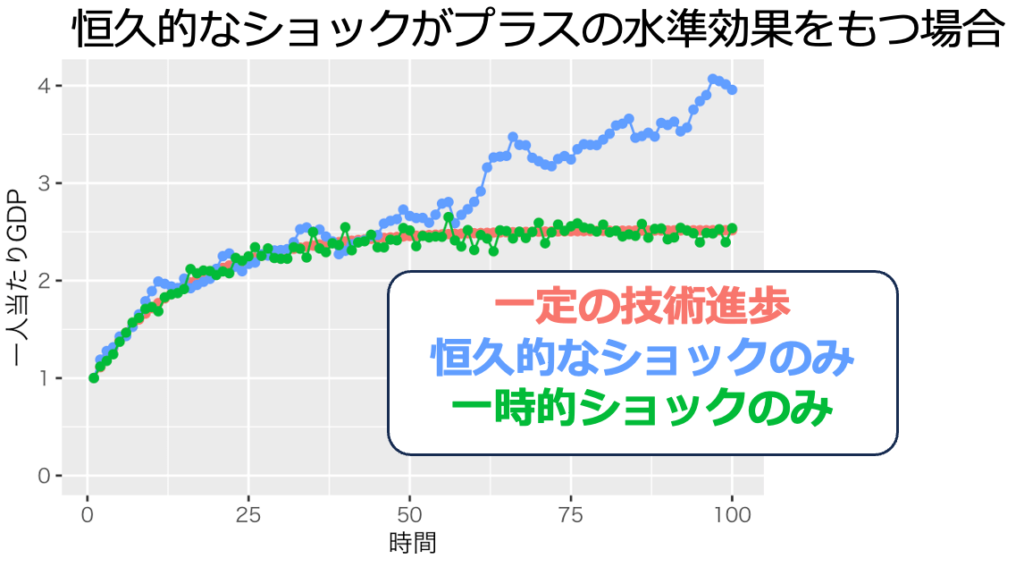
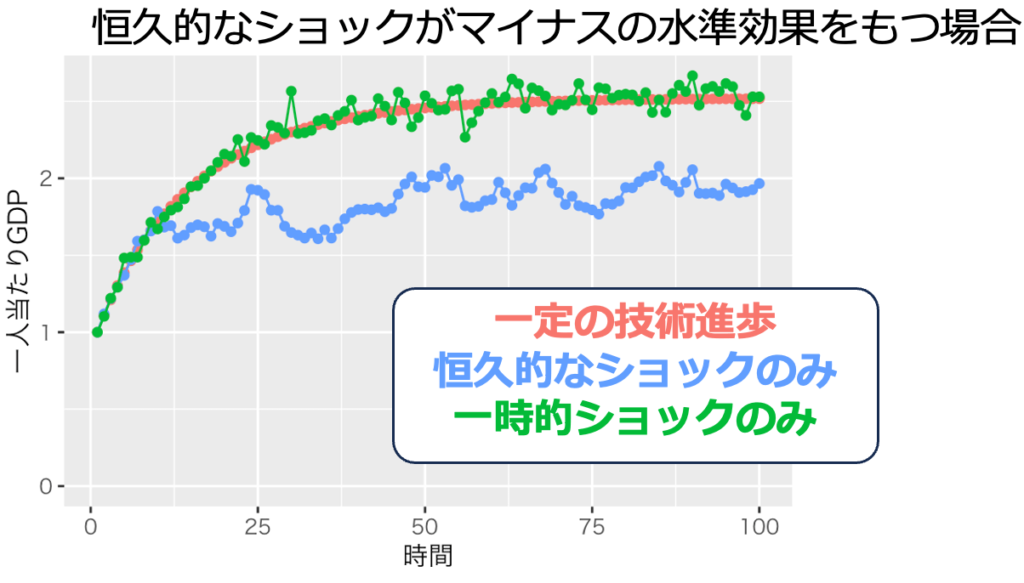
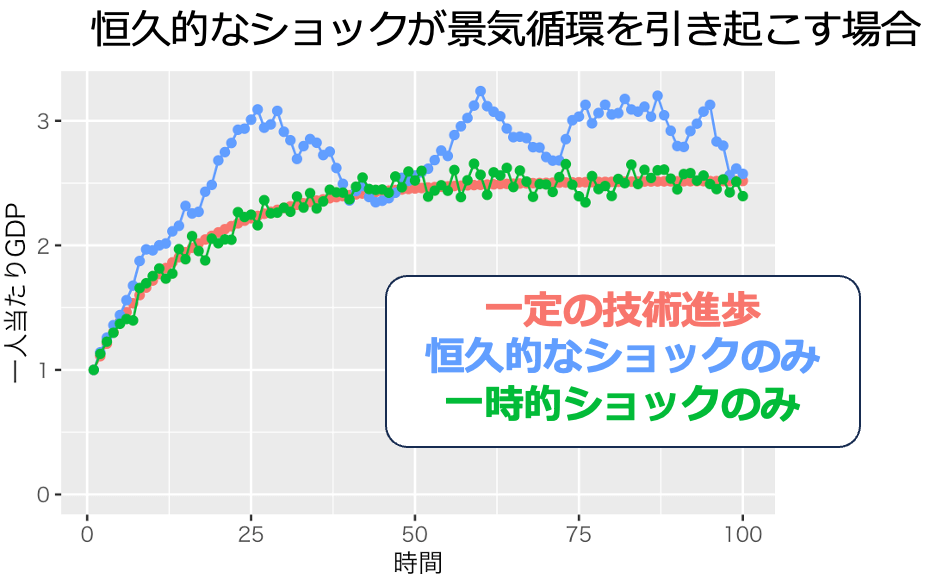
　確率的なショックが恒久的なのか一時的なのかは重大な問題である。ショックが次の期に影響を及ぼす恒久的なショックの場合、ある期においてプラスのショックを与えれば長期的な経済状態を改善できる。経済政策担当者は、日本経済に恒久的にプラスとなる政策ショックを与えてほしい。

　

【追記】

・動学的確率的モデル

　このソロー・モデルは動学的確率的モデル（Dynamic stochastic model）である。一般均衡は用いいていないので、動学的確率的一般均衡（DSGE, Dynamic stochastic general equilibrium）とは異なる。

・シミュレーションのRコード

#変数説明
#Y=国全体GDP、国全体の資本=K、A=技術係数、L=労働L
#y=「一人」当たりGDP、c=一人当たり消費、k=一人当たり資本
　
#パラメーター
s <- 0.4 #貯蓄率
alpha <- 0.4 #資本分配率
d <- 0.1 #資本減耗率
n <- 0 #人口成長率
g <- 0 #技術進歩率(基本)
sd <- 0.05 #技術的ショックの標準偏差
　
#初期値
A1 <- 1
L1 <- 1
K1 <- 1
　
#資本の遷移式
NextKapital <- function(K,Y,s,d) {
  K_next <- K + s*Y - d*K
  return(K_next)
}
　
#マクロ生産関数(国全体)
GDP <- function(K,A,L,alpha) {
  Y <- (K^alpha)*((A*L)^(1-alpha)) 
  return(Y)
}
　
#定率の技術進歩
NextA_deterministic <- function(A,g) {
  A_next <- (1+g)*A
  return(A_next)
}
　
#技術係数の確率的変動関数
NextA_stochastic <- function(A,g) {
  Stochastic_shock <- rnorm(1,0,sd) #平均0、標準偏差gの乱数を1個生成
  A_next <- (1+g)*A+Stochastic_shock*(1+g)*A
  return(A_next)
}
　
#行列準備
T <- 100　#シミュレーション期間
Data<-  data.frame(matrix(0,T,14))
colnames(Data) <- c("time","L",
                    "Y_constant","K_constant","A_constant","y_constant",
                    "Y_permanent","K_permanent","A_permanent","y_permanent",
                    "Y_transitory","K_transitory","A_transitory","y_transitory")
　
#初期値
Data[1,"time"] <- 1
Data[1,"L"] <- L0
Data[1,"A_constant"] <- A1
Data[1,"K_constant"] <- K1
Data[1,"A_permanent"] <- A1
Data[1,"K_permanent"] <- K1
Data[1,"A_transitory"] <- A1
Data[1,"K_transitory"] <- K1
　
#シミュレーション（1期から(T-1)期まで）
for(t in 1:(T-1) ){
  L <- Data[t,"L"]
  A_constant <- Data[t,"A_constant"]
  K_constant <- Data[t,"K_constant"]
  A_permanent <- Data[t,"A_permanent"]
  K_permanent <- Data[t,"K_permanent"]
  A_transitory <- Data[t,"A_transitory"]
  K_transitory <- Data[t,"K_transitory"]  
  
  Y_constant <- GDP(K_constant,A_constant,L,alpha)
  Y_permanent <- GDP(K_permanent,A_permanent,L,alpha)
  Y_transitory <- GDP(K_transitory,A_transitory,L,alpha)
  
  Data[t,"Y_constant"] <- Y_constant
  Data[t,"y_constant"] <- Y_constant/L
  Data[t,"Y_permanent"] <- Y_permanent
  Data[t,"y_permanent"] <- Y_permanent/L
  Data[t,"Y_transitory"] <- Y_transitory
  Data[t,"y_transitory"] <- Y_transitory/L
  
  Data[t+1,"time"] <- 1 + Data[t,"time"]
  Data[t+1,"L"] <- (1+n)*L
  Data[t+1,"A_constant"] <- NextA_deterministic(Data[t,"A_constant"],g)
  Data[t+1,"A_permanent"] <- NextA_stochastic(Data[t,"A_permanent"],g)
  Data[t+1,"A_transitory"] <- NextA_stochastic(Data[t,"A_constant"],g) #ここをA_constantにしたのが重要
  Data[t+1,"K_constant"] <- NextKapital(K_constant,Y_constant,s,d)
  Data[t+1,"K_permanent"] <- NextKapital(K_permanent,Y_permanent,s,d)
  Data[t+1,"K_transitory"] <- NextKapital(K_transitory,Y_transitory,s,d)
}
　
#最終期のデータ補完
Data[T,"Y_constant"] <- GDP(Data[T,"K_constant"],Data[T,"A_constant"],Data[T,"L"],alpha)
Data[T,"y_constant"] <- Data[T,"Y_constant"]/Data[T,"L"]
Data[T,"Y_permanent"] <- GDP(Data[T,"K_permanent"],Data[T,"A_permanent"],Data[T,"L"],alpha)
Data[T,"y_permanent"] <- Data[T,"Y_permanent"]/Data[T,"L"]
Data[T,"Y_transitory"] <- GDP(Data[T,"K_transitory"],Data[T,"A_transitory"],Data[T,"L"],alpha)
Data[T,"y_transitory"] <- Data[T,"Y_transitory"]/Data[T,"L"]
　
#描画
plot(Data$time,Data$表示したい変数名)
plot(Data$time,Data$y_transitory)　#国全体のGDP(Y)の描画
　
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
　
ggplot(Data, aes(x = time))+
  geom_line(aes(y = y_constant,colour = "一定の技術進歩"))+
  geom_point(aes(y = y_constant,colour = "一定の技術進歩"))+
  geom_line(aes(y = y_permanent,colour = "恒久的なショックのみの技術進歩"))+
  geom_point(aes(y = y_permanent,colour = "恒久的なショックのみの技術進歩"))+
  geom_line(aes(y = y_transitory,colour = "一時的なショックがある技術進歩"))+
  geom_point(aes(y = y_transitory,colour = "一時的なショックがある技術進歩"))+
  labs(color = "凡例")+
  xlab("時間") + 
  ylab ("一人当たりGDP") +
  theme_grey(base_family = "HiraKakuPro-W3")+
  ylim(c(0, NA))