CRRA効用関数(Constant Relative Risk Aversion Utility Function, 相対的リスク回避度一定効用関数)とは、次の関数である。相対的リスク回避度とは、次の式で表せ、効用関数の曲がり具合についての概念である。
$$U(X)=\frac{ X^{1-\sigma }}{1-\sigma } ただし\sigma≠1$$
$$U(X)=\log (X) ただし\sigma=1$$
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}=\sigma$$
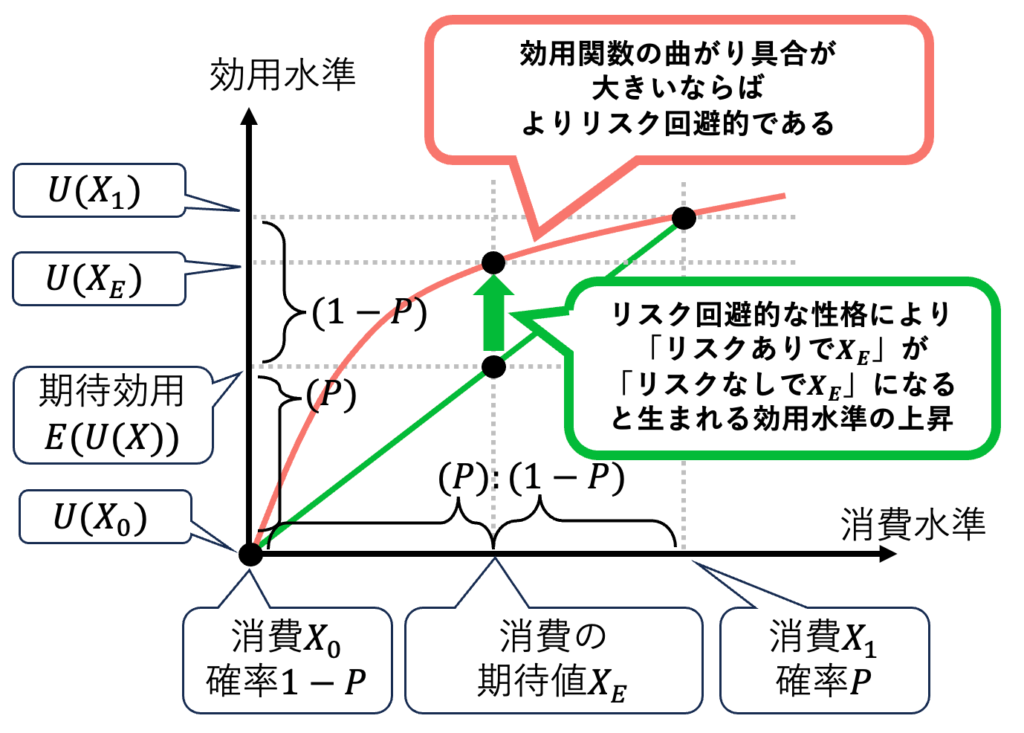
リスクとは、計算可能な不確実性である。例えば「消費Xができる確率がP」「消費が0になる確率が1-P」の場合、リスクが存在する。消費の期待値E(X)と効用の期待値E(U)は、計算可能である(図1)。リスクを避けるタイプの場合、「リスクがある中で平均的にE(X)を消費できる計画」よりも「リスクなしで確実にE(X)を消費できる計画」を好む。このリスク回避の度合いが図1の緑の矢印の長さである。これが長いということは、効用関数の曲がり具合が強く、限界効用が逓減する度合いU”(X)が強いことを意味する。相対的リスク回避度(RRA、Relative Risk Aversion)は「消費Xが1%変わったときに限界効用が何%変わるか」と定義される。
$$相対的リスク回避度=\frac{限界効用の変化率}{消費の変化率}$$
CRRA型効用関数は、動学的最適化を考えるマクロ経済学でよく使われる。定常状態で一定の金利を持つ場合、限界効用の成長率は一定でなければならない。定常状態で一定の金利を持つようにモデルをセッティングするならば、「消費Xが1%変わったときでも限界効用の変化率は一定」つまり相対的リスク回避度が一定の効用関数でなければならない。
【問題】
問1【グラフ】式1のように分子にマイナス1をつけるCRRA型効用関数も存在する。σ=0.6のCRRA型効用関数について考えよう。式2と式3をGeoGebraの関数グラフ機能を用いて図示せよ(1)。式3のように分子にマイナス1をつけるとどんないいことがあるか述べよ。(2)
$$式1:U(X)=\frac{ X^{1-\sigma } -1 }{1-\sigma }$$
$$式2:U(X)=\frac{ X^{1-\sigma }}{1-\sigma }=0.6 X^{0.4}$$
$$式3:U(X)=\frac{ X^{1-\sigma }-1}{1-\sigma }=0.6 X^{0.4}-0.6$$
問2【限界効用】CRRA型効用関数の限界効用(MU, merginal utiliry)を求めよ。(相対的リスク回避度σ≠1)
$$U(X)=\frac{ X^{1-\sigma }}{1-\sigma }$$
問3【限界効用】相対的リスク回避度σ=1のCRRA型効用関数、つまり、Log型効用関数の限界効用(MU, merginal utiliry)を求めよ。
$$U(X)=\log (X)$$
問4【パラメーターσ】相対的リスク回避度(RRA、Relative Risk Aversion)を「消費Xが1%変わったときに限界効用が何%変わるか」と定義したときに、次の式が導けることを示せ。
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}$$
問5【パラメーターσ】次の相対的リスク回避度(RRA、Relative Risk Aversion)を言葉を使って直感的に説明せよ。その際は「リスク回避度が大きいとは、効用関数の曲がり具合が強く、限界効用が逓減する度合いU”(X)が強い」という直感を用いて良い。
問6【パラメーターσ】CRRA型効用関数が相対的リスク回避度一定のことを示せ。
【解答】
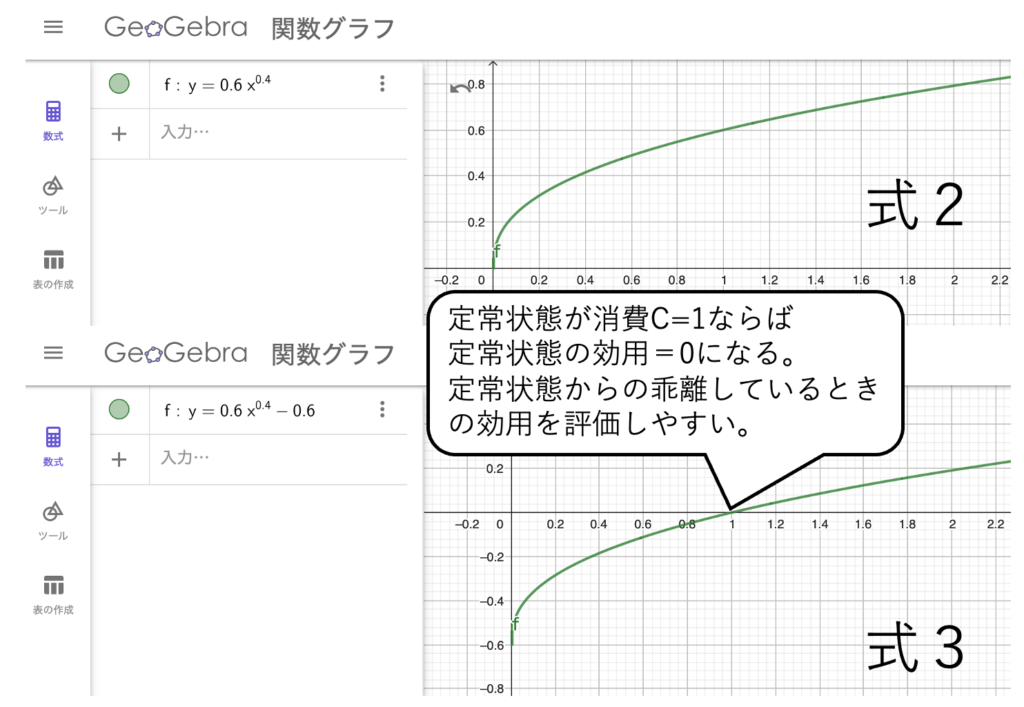
問1【グラフ】式1のように分子にマイナス1をつけるCRRA型効用関数も存在する。σ=0.6のCRRA型効用関数について考えよう。式2と式3をGeoGebraの関数グラフ機能を用いて図示せよ(1)。式3のように分子にマイナス1をつけるとどんないいことがあるか述べよ。(2)
$$式1:U(X)=\frac{ X^{1-\sigma } -1 }{1-\sigma }$$
$$式2:U(X)=\frac{ X^{1-\sigma }}{1-\sigma }=0.6 X^{0.4}$$
$$式3:U(X)=\frac{ X^{1-\sigma }-1}{1-\sigma }=0.6 X^{0.4}-0.6$$
問2【限界効用】CRRA型効用関数の限界効用(MU, merginal utiliry)を求めよ。(相対的リスク回避度≠1)
$$U(X)=\frac{ X^{1-\sigma }}{1-\sigma }$$
$$U'(X)=\frac{ (1-\sigma)X^{-\sigma }}{1-\sigma }=X^{-\sigma }$$
問3【限界効用】相対的リスク回避度=1のCRRA型効用関数、つまり、Log型効用関数の限界効用(MU, merginal utiliry)を求めよ。
$$U(X)=\log (X)$$
$$U'(X)=\frac{1}{X}=X^{-1}=X^{- \sigma } なぜなら\sigma=1$$
問4【パラメーターσ】相対的リスク回避度(RRA、Relative Risk Aversion)を「消費Xが1%変わったときに限界効用が何%変わるか」と定義したときに、次の式が導けることを示せ。
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}$$
$$相対的リスク回避度=\frac{限界効用の変化率}{消費の変化率}$$
$$=\frac{ \left[ \frac{ \left( – \frac{ d U'(X)}{d X} \right) }{U'(X)} \right] }{ \left[ \frac{d X}{ X} \right] }=\frac{ \frac{- d U'(X)}{U'(X)}}{\frac{1}{X}}= – \frac{X U ‘ ‘ (X)}{U'(X)}$$
問5【パラメーターσ】次の相対的リスク回避度(RRA、Relative Risk Aversion)を言葉を使って直感的に説明せよ。その際は本文にあるように「リスク回避度が大きいとは、効用関数の曲がり具合が強く、限界効用が逓減する度合いU”(X)が強い」という直感を用いて良い。
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}$$
リスク回避度は、限界効用が逓減する度合いU”(X)の大きさで評価できる。しかし、U”(X)だけだと問題が生まれる。U”(X)<0なので、大小関係を一致させるために、マイナスをかけてやる。U”(X)の絶対量だけで評価すると、U'(X)が大きい場合とU'(X)が小さい場合で比較ができないので、U'(X)で割って相対量で評価する。また、Xが大きい場合とXが小さい場合を比較できるようにするために、Xをかけてやる。すると、リスク回避度を測る適切な指標としての相対的リスク回避度(RRA、Relative Risk Aversion)が完成する。
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}$$
問6【パラメーターσ】CRRA型効用関数が相対的リスク回避度一定のことを示せ。
$$問1よりU'(X)=X^{-\sigma }$$
$$よってU”(X)=-\sigma X^{-\sigma -1}であるので$$
$$相対的リスク回避度=- \frac{X U ‘ ‘ (X)}{U'(X)}$$
$$=- \frac{X (-\sigma X^{-\sigma -1})}{X^{-\sigma }}=\sigma$$
