この記事ではR言語で動学モデルのシミュレーションを行う方法を解説する。この内容がわかれば、人口成長モデル、感染症モデル、経済成長モデル、景気循環モデルのシミュレーションができるようになる。動学モデルとは、1期、2期、3期・・・と時間によって状態が変化するモデルである。t期の状態が決まると、t+1期の状態が決まる決定論的なモデルをRでシミュレーションする方法について解説する。具体例として、次のマルサス型人口成長モデルを考える。1945期の人口が25(億人)、人口成長率が1.5%で、2030期までの86期にわたる人口成長をシミュレーションしてみよう。
$$動学モデル:N_{t+1}=(1+n)N_t$$
$$N:人口、n:人口成長率(=0.015)$$
$$人口の初期値:N_1=25億人(1945年)$$
動学モデルのプログラムを考えてみよう。このプログラムは、大きく4つの手順に分けられる。第一に、数値や関数を設定する。第二に、出力結果を格納するためのデータフレームを準備する。第三に、86回の繰り返し処理で関数を実行する。第四に、出力結果を表やグラフ形式で確認する。以上の4つである。

以上のプログラムをRコードにして、実行すると、次のような画面になる。ちなみに、「世界人口白書2023」によれば2023年の世界人口は80億4500万人で、このシミュレーションによれば79億8500万人である。

#数値の設定
T <- 86 #シミュレーション期間
time1 <- 1945 #期間の初期値
N1 <- 25 #変数の初期値
n <- 0.015 #パラメーター
#関数の設定 Nを入力すると(1+n)Nが出力される関数func
func <- function(N) {
nextN <- (1+n)*N
return(nextN)
}
#データフレームの設定
Data <- data.frame(matrix(0,T,2)) #2列T行ですべてのデータが0のデータフレームを作成
colnames(Data) <- c("time","N") #1列目の名前をtime、2列目の名前をNに変更
Data[1,"time"] <- time1 #初期値の代入
Data[1,"N"] <- N1 #初期値の代入
#繰り返し処理シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1) ){
time <- Data[t,"time"] #Dataのt行目time列のデータ呼び出して、timeと名付ける
N <- Data[t,"N"] #Dataのt行目N列のデータ呼び出して、Nと名付ける
Data[t+1,"time"] <- time + 1 #timeに1を足してDataのt+1行目time列に書き込む
Data[t+1,"N"] <- func(N) #Nを関数funcに入力して、出力結果をt+1行目N列に書き込む
}
#出力結果
Data #表
plot(Data$time,Data$N) #散布図グラフ
#plot(横軸,縦軸) #データフレーム$変数名
#gglpotを用いた綺麗な作図
install.packages("ggplot2") #作図パッケージのインストール(2回目以降は必要なし)
library(ggplot2) #ggplot2の起動
ggplot(Data)+
geom_line(aes(x = time, y = N))+ #折れ線グラフ
geom_point(aes(x = time, y = N))+ #散布図
xlab("年数") + #横軸のラベル
ylab ("人口") + #縦軸のラベル
ggtitle ("世界人口のシミュレーション") + #グラフのタイトル
theme_grey(base_family = "HiraKakuPro-W3") #日本語フォント設定
【補足】
・マルサス型人口成長モデルについて
マルサスは「人口は制限されなければ指数関数的に増加するが、生活資源は直線的にしか増加しないので、生活資源は必ず不足する」という「マルサスの罠」で有名。この記事では「人口が指数関数的に増加する」というマルサス型人口成長モデルを扱った。
ところで、なぜ人口は指数関数的に増えるのだろうか? マルサスによれば「異性間の情欲には歯止めが効かないから」だそうだ。なるほど・・・?
性欲と人口成長の関係は傍に置くとして、実際に、ここ200年、世界人口はマルサス型人口成長モデルと同じような爆発的な人口成長期を迎えている。
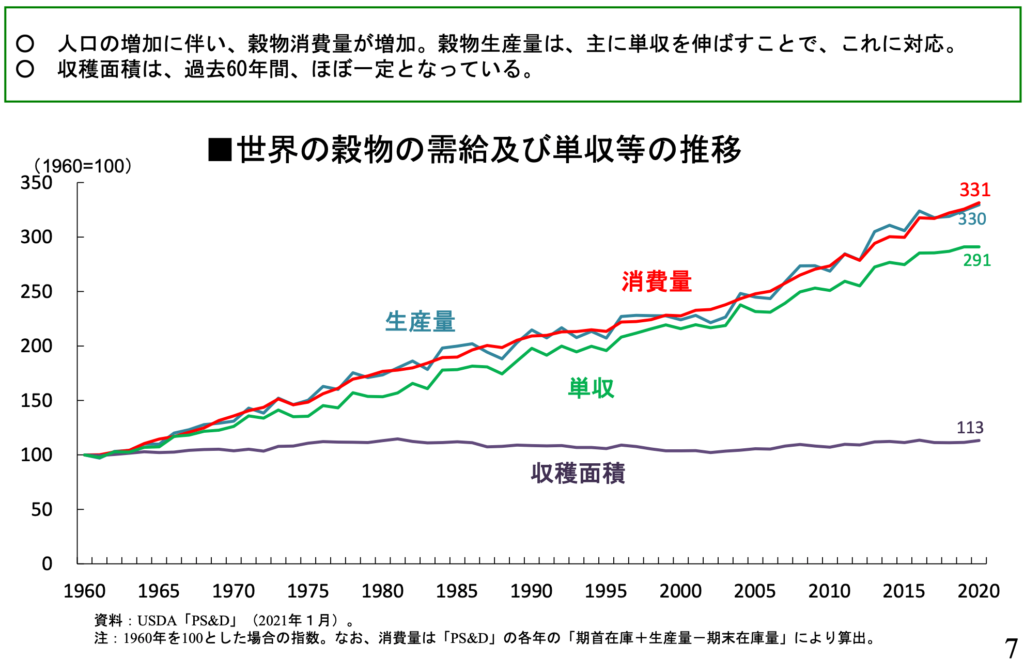
問題は「なぜマルサスの罠に陥っていないのか?」である。答えは「技術進歩のおかげ」である。農業に目を向けると、1960年から現在にかけて、農地の増加はほぼないが、農地1単位当たりの収量が伸びている(下図)。つまり、技術進歩が人口成長を支えた。ここ200年のスパンで見ると「ハーバー・ボッシュ法による窒素の化学肥料の誕生」という技術進歩が重要であったとされる。
ちなみに、ソロー・モデルにもマルサス型人口成長モデルが組み込まれている。ソロー・モデルも「マルサスの罠」を回避しており、技術進歩の重要性を強調する。
