宇宙の物理法則は、人類が抱く最もスケールの大きな問いの一つだ。宇宙の物理法則についての歴史上最も印象的な事件は、天動説(Geocentrism)から地動説(Heliocentrism)への転回である。天動説とは、地球が宇宙の中心にあって、他のすべての天体はその周りを公転するとして説明するモデルである。地動説とは、惑星は中心にある太陽の周りを公転するとして説明するモデルである。天動説は、2つの意味で優れていた。第一に、我々は大地が動いていないように感じ、多くの天体は地球を回っているように観測できるので、直感的に正しい。第二に、神が地球を創造したというキリスト教教義を信じるのならば、地球が宇宙の中心であると考える学説は、神学的に望ましい。
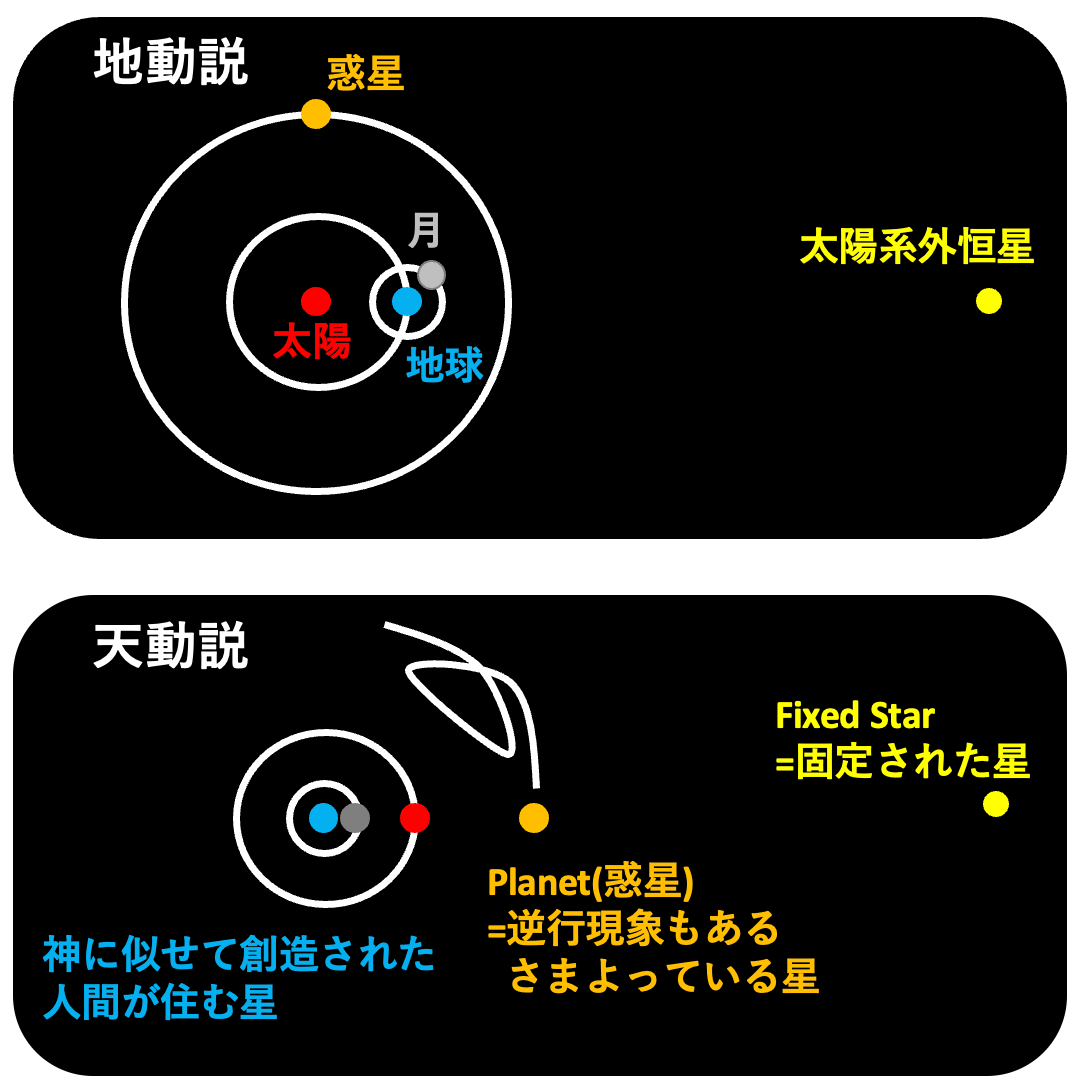
日本人は地球が太陽を公転するというモデルを学校で教わっているので、天動説が誤っていると考える。ところで地動説と天動説での軌道をシミュレーションしてみたことはあるだろうか。地動説に基づき星の運行をシミュレーションし、地球視点での運行に変換して天動説の軌道と見なした。画像2を見ると、地動説モデルはたしかに美しい。天動説モデルがもつ複雑性が緩和されている。しかし、同じように天体の運行を求められるのならば、天動説モデルは別解として成り立つのではないかという気もしてくる。
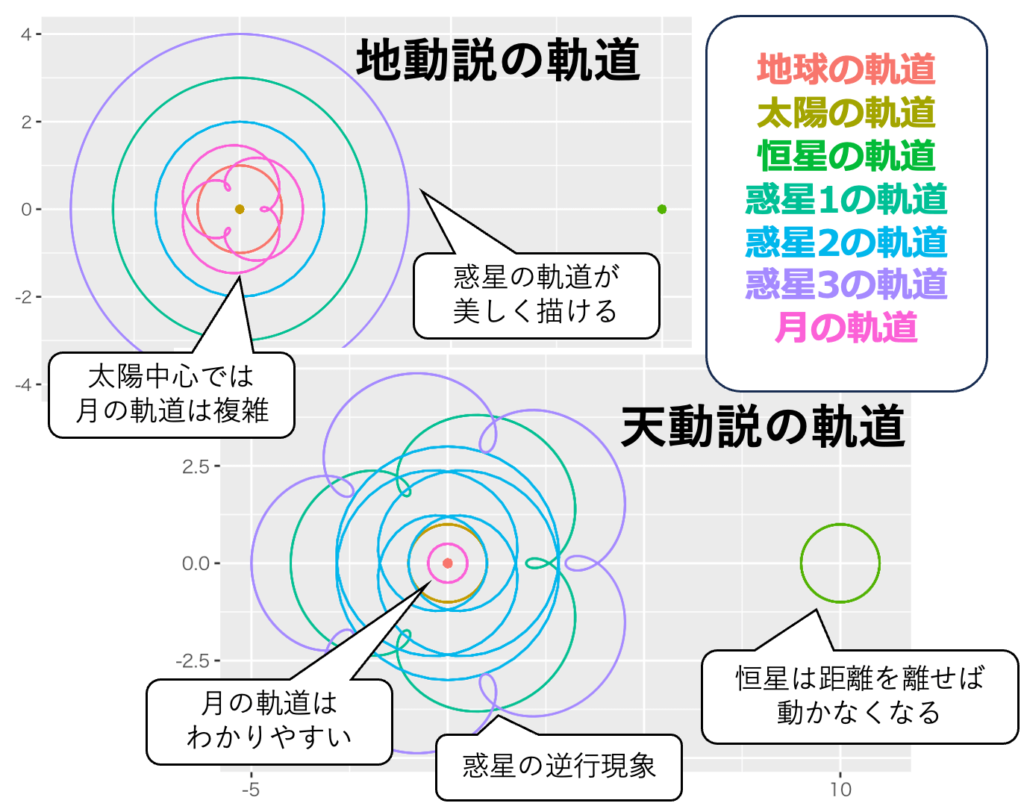
【モデル】
$$地動説:(X_t,Y_t)=(r \cos (w t),r \sin (w t))$$
$$天動説:(X_t,Y_t)=(r \cos (w t)-X_t^{地球},r \sin (w t)-Y_t^{地球})$$
$$r:半径、w:角速度、t:時間$$
近世ヨーロッパにて宇宙論がなぜ転回したのか(=コペルニクス的転回)については、データ分析、理論、世代交代の観点が重要である。天動説は1000年に渡って正統学説として支持されたが、当時の観測では、天動説モデルの予測力は高く、データ分析上の問題はなかった。さらに、神が神に似せて人間を造ったのならば、その地球を中心に宇宙が回っているというのは「美しい理論」なのである。天動説は、データ分析と理論によって崩れ、世代交代によって影響力を失った。データ分析面では、望遠鏡を用いてガリレオが木星を公転する衛星を見つけたことによって、すべての星が地球の周りを回っていないことが示された。理論面では、ニュートンが運動の3法則を公理とすると、ユークリッドの『幾何原論』の論証法で、地上の小物体の運動から天体の運行までを統一的に説明できる「美しい理論」を示した。そして、宇宙観が天動説から地動説へと移ったのは、かつての天動説信者が死に絶えて、地動説の支持者へと人口構成が変わっていったからである。
おすすめ漫画『チ。』
天動説が支配的なキリスト教社会にて地動説に魅せられた人々を描いたマンガ『チ。―地球の運動について―』はおすすめです。

ニュートン『プリンキピア』
アイザック・ニュートンは1687年に『プリンキピア(Philosophiæ Naturalis Principia Mathematica、自然哲学の数学的諸原理)』にて、運動の3法則を「公理」として仮定すると、地球上の小物体の運動と天体の運行が統一的に説明できることを証明した。具体的には「2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用する」という「万有引力の法則」を導き、さらにそこからケプラーが発見した楕円の天体の運動を導いた。これは地動説の見解であった。
プリンキピアは、まず公理を仮定し、それを幾何学的に証明するという『原論』(古代エジプトの幾何学者ユークリッドの本)の手法に基づいて議論が展開される。ニュートンは微分積分を創始したことでも有名だが、微積の功績についてライプニッツと係争中であり、プリンキピアでの証明に微積は使われなかった。高校数学では、いまだにニュートン力学が教えられている。
学説史
・古代ギリシア:アリスタルコス(前310 – 前230)が地動説を主張した。
・古代ローマ:プトレマイオス(83 – 168)が『アルマゲスト』で天動説を精緻なモデルにした。このプトレマイオスの天動説が1000年近くヨーロッパで信じられた。
・1543年:ニコラウス・コペルニクス(1473 – 1543)は、死後に発表した『天球の回転について』で地動説を唱えた。コペルニクスから始まる人類の宇宙観の大転換を「コペルニクス的転回」と呼ぶ。
・1600年:地動説を唱えたジョルダーノ=ブルーノはローマ教会によって異端審問にかけられ処刑された。
・1609年:ヨハネス・ケプラーが軌道が楕円であることを発見し、天体運動をモデル化した。(ケプラーの第一法則)
・1616年、1633年:望遠鏡での観測結果に基づき、地動説を唱えたガリレオ・ガリレイは、2度も異端審問にかけられた。
・1687年:アイザック・ニュートンが、運動の3法則から万有引力を導き、ケプラーの法則を説明できることを証明した。
・1992年:ローマ教皇ヨハネ・パウロ2世はガリレオ裁判の誤りを認め、公式に謝罪。
・2014年:科学誌『サイエンス』を発行する米国科学振興協会(AAAS)は、2200人以上の米国人を対象に調査し、およそ4人に1人は地球が太陽の周りを公転していることを知らなかったとの結果を年次会合にて報告した。(出典:AFP通信)
・2020年:天動説が支配的なキリスト教社会にて地動説に魅せられた人々を描いたマンガ『チ。―地球の運動について―』の第1集が発売された。
プログラミング・メモ
シミュレーションに用いたRコード↓
T <- 1000 #期
#パラメーター
r1 <- 1 #地球と太陽の距離
w1 <- pi*(12/360) #地球の公転角速度
r2 <- 3 #太陽と惑星の距離
w2 <- pi*(3/360) #惑星の公転角速度 5/360が良い
r3 <- 0.5 #地球と月の距離
w3 <- pi*(30/360) #月の公転角速度
r4 <- 2 #惑星2と月の距離
w4 <- pi*(20/360) #惑星2の公転角速度
r5 <- 4 #惑星2と月の距離
w5 <- pi*(2/360) #惑星2の公転角速度
star_distance <- 10 #恒星と太陽の距離
#初期値
Data<- data.frame(matrix(0,T,24))
colnames(Data) <- c("sun_x_sun","sun_y_sun","earth_x_sun","earth_y_sun","planet1_x_sun","planet1_y_sun","planet2_x_sun","planet2_y_sun","planet3_x_sun","planet3_y_sun","moon_x_sun","moon_y_sun","sun_x_earth","sun_y_earth","earth_x_earth","earth_y_earth","planet1_x_earth","planet1_y_earth","planet2_x_earth","planet2_y_earth","planet3_x_earth","planet3_y_earth","moon_x_earth","moon_y_earth")
#シミュレーション
for(t in 1:(T) ){
#地動説
Data[t,"sun_x_sun"] <- 0
Data[t,"sun_y_sun"] <- 0
Data[t,"earth_x_sun"] <- r1*cos(w1*t)
Data[t,"earth_y_sun"] <- r1*sin(w1*t)
Data[t,"planet1_x_sun"] <- r2*cos(w2*t)
Data[t,"planet1_y_sun"] <- r2*sin(w2*t)
Data[t,"planet2_x_sun"] <- r4*cos(w4*t)
Data[t,"planet2_y_sun"] <- r4*sin(w4*t)
Data[t,"planet3_x_sun"] <- r5*cos(w5*t)
Data[t,"planet3_y_sun"] <- r5*sin(w5*t)
Data[t,"moon_x_sun"] <- r1*cos(w1*t)+ r3*cos(w3*t)
Data[t,"moon_y_sun"] <- r1*sin(w1*t)+ r3*sin(w3*t)
Data[t,"fixed_star_x_sun"] <- star_distance
Data[t,"fixed_star_y_sun"] <- 0
#地球視点へ
Data[t,"sun_x_earth"] <- -Data[t,"earth_x_sun"]
Data[t,"sun_y_earth"] <- -Data[t,"earth_y_sun"]
Data[t,"earth_x_earth"] <- 0
Data[t,"earth_y_earth"] <- 0
Data[t,"planet1_x_earth"] <- Data[t,"planet1_x_sun"]-Data[t,"earth_x_sun"]
Data[t,"planet1_y_earth"] <- Data[t,"planet1_y_sun"]-Data[t,"earth_y_sun"]
Data[t,"planet2_x_earth"] <- Data[t,"planet2_x_sun"]-Data[t,"earth_x_sun"]
Data[t,"planet2_y_earth"] <- Data[t,"planet2_y_sun"]-Data[t,"earth_y_sun"]
Data[t,"planet3_x_earth"] <- Data[t,"planet3_x_sun"]-Data[t,"earth_x_sun"]
Data[t,"planet3_y_earth"] <- Data[t,"planet3_y_sun"]-Data[t,"earth_y_sun"]
Data[t,"moon_x_earth"] <- Data[t,"moon_x_sun"]-Data[t,"earth_x_sun"]
Data[t,"moon_y_earth"] <- Data[t,"moon_y_sun"]-Data[t,"earth_y_sun"]
Data[t,"fixed_star_x_earth"] <- Data[t,"fixed_star_x_sun"]-Data[t,"earth_x_sun"]
Data[t,"fixed_star_y_earth"] <- Data[t,"fixed_star_y_sun"]-Data[t,"earth_y_sun"]
}
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#地動説
ggplot(Data)+
geom_path(aes(x = sun_x_sun,y = sun_y_sun,colour = "太陽"))+
geom_point(aes(x = sun_x_sun,y = sun_y_sun,colour = "太陽"))+
geom_path(aes(x = earth_x_sun,y = earth_y_sun,colour = "地球"))+
geom_path(aes(x = planet1_x_sun,y = planet1_y_sun,colour = "惑星1"))+
geom_path(aes(x = planet2_x_sun,y = planet2_y_sun,colour = "惑星2"))+
geom_path(aes(x = planet3_x_sun,y = planet3_y_sun,colour = "惑星3"))+
geom_path(aes(x = moon_x_sun,y = moon_y_sun,colour = "月"))+
geom_path(aes(x = fixed_star_x_sun,y = fixed_star_y_sun,colour = "恒星"))+
geom_point(aes(x = fixed_star_x_sun,y = fixed_star_y_sun,colour = "恒星"))+
theme_grey(base_family = "HiraKakuPro-W3")+
labs(color = "凡例")+
xlab("X軸") +
ylab ("Y軸")
#天動説
ggplot(Data)+
geom_path(aes(x = sun_x_earth,y = sun_y_earth,colour = "太陽"))+
geom_path(aes(x = earth_x_earth,y = earth_y_earth,colour = "地球"))+
geom_point(aes(x = earth_x_earth,y = earth_y_earth,colour = "地球"))+
geom_path(aes(x = planet1_x_earth,y = planet1_y_earth,colour = "惑星1"))+
geom_path(aes(x = planet2_x_earth,y = planet2_y_earth,colour = "惑星2"))+
geom_path(aes(x = planet3_x_earth,y = planet3_y_earth,colour = "惑星3"))+
geom_path(aes(x = moon_x_earth,y = moon_y_earth,colour = "月"))+
geom_path(aes(x = fixed_star_x_earth,y = fixed_star_y_earth,colour = "恒星"))+
theme_grey(base_family = "HiraKakuPro-W3")+
labs(color = "凡例")+
xlab("X軸") +
ylab ("Y軸")