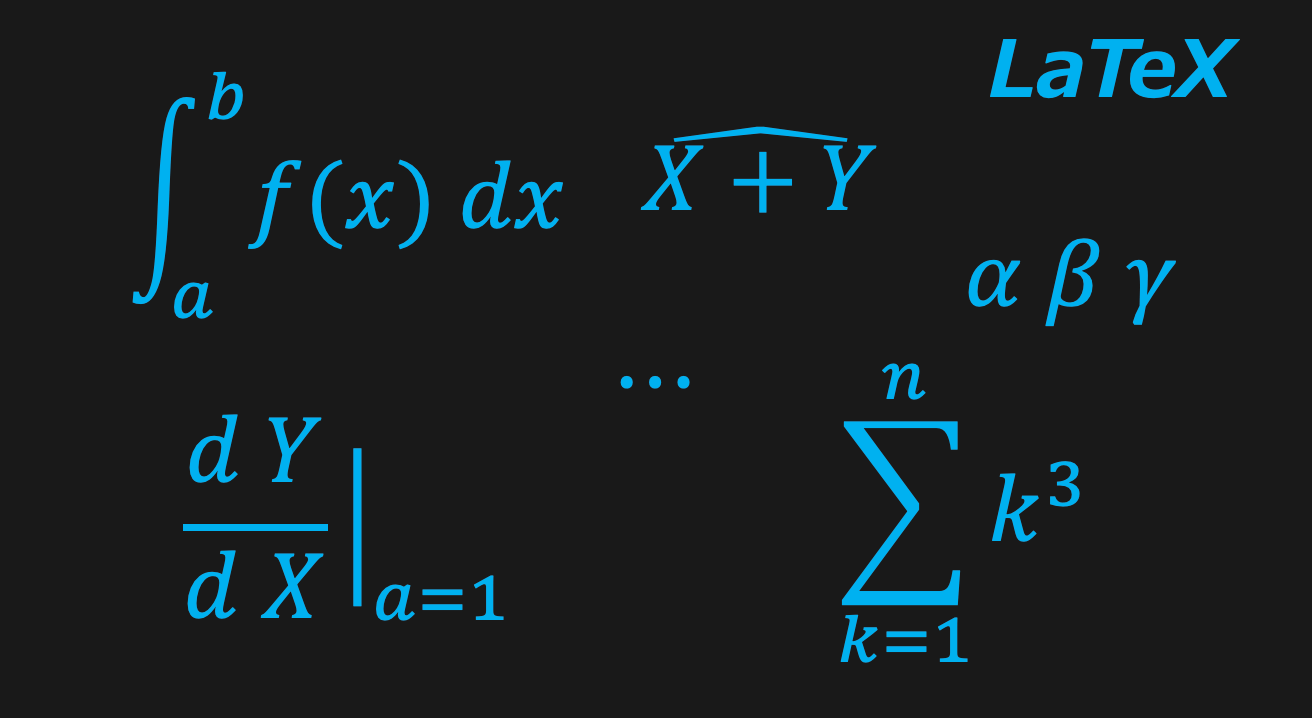LaTeX(ラーテック)(通称:ラテフ)の環境構築、数式表現のコードについて、ご紹介します。
$$\LaTeX$$
#LaTeXのロゴを表示するLaTeXコード
\LaTeXLaTeXについて
LaTeXを使うと美しい数式表現が可能です。例えば、こんな感じです↓
ベタ打ち→e=lim n→∞ (1+1/n)^n 醜い!
$$e = \lim_{n \to \infty} \Big(1 + \frac{1}{n} \Big)^n →美文字$$
ところでLaTeXはどう読むのでしょうか? いくつかの流派があります。
・ラーテック(Lah-tech)、レイテック(Lay-tech):英語圏で使われる発音。(出典:Introduction to LaTeX)
・ラテフ:日本人独特の読み方。LaTeX(1989年)のもとになったTeX(1978年)がテフと読まれていたから。テフはギリシア語風の読み方。
・フランス語ではla-tek、ドイツ語ではlah-tekhs
LaTeXの環境構築
LaTeXは次の場所で使うことができます。
・【おすすめ】Word / PowerPoint(挿入→数式で使える。なお、パワポでは、描画→フリーハンドで数式を書く→オブジェクト選択→「インクを演算に変換」でLaTeX化できる。パワポの数式はWordにコピペ可。LaTeXを勉強するのが割に合わないと思う人は、ノーコードで綺麗な数式を書いてみよう! iPadやペンタブ所持者におすすめ。)
・【おすすめ】Cloud LaTeX(クラウドでLaTeXを使える。日本の学生アプリコンテスト出品作品。現在はアカリクが運営。テンプレ使うとすぐに日本語を書けるの偉い。2014年〜)(出典:Cloud LaTeXを語る ―大人気サービスの誕生秘話―)
・Overleaf(クラウドでLaTeXを使える。全世界で使われている。前身は2011年〜)(出典:Wikipedia)
・RMarkdown(Rでの文書化で使える。)
・MathJax(数式をウェブブラウザ上で表示するJavaScriptライブラリ。しまうま総研も使用。)
LaTeXで文書作成
Cloud LaTeXの「新規プロジェクト」から「既定テンプレートのプロジェクト」を新規作成するのがおすすめです。日本語ユーザーに優しいからです。ただ、Overleafもよく使われています。
\RequirePackage{plautopatch} %おまじない:非互換な海外製パッケージが使われた場合には自動で検知して適切なパッチを読み込む
\RequirePackage[l2tabu, orthodox]{nag} %古いコマンドやパッケージの利用を警告
\documentclass[platex,dvipdfmx]{jlreq} % platexの日本語のため
\usepackage{graphicx} % 画像取り込み
\title{レポートタイトル} %レポートタイトル
\author{著者名} %著者名
\date{\today} %今日の日付
\begin{document} %ここから文書始まる
\maketitle %タイトル、著者名、日付の出力
本文入力。
$$\frac{1}{2}$$
\end{document} %ここで文書終わるLaTeXで数式を書く
#数式の書き方 ※どのサービスでLaTeXを使うかで異なる。
$数式$ #文章中で数式を書く場合
$$数式$$ #1行使って数式を書く場合
#バックスラッシュについて
\と¥は同じ主なギリシア文字(小文字)
$$\alpha, \beta, \gamma, \delta, \epsilon, \zeta, \mu, \pi, \rho, \theta, \lambda, \sigma, \phi, \omega$$
#α アルファ
\alpha
#β ベータ
\beta
#γ ガンマ
\gamma
#δ デルタ
\delta
#ε イプシロン
\epsilon
#ζ ゼータ
\zeta
#μ ミュー
\mu
#π パイ
\pi
#ρ ロー
\rho
#θ シータ
\theta
#λ ラムダ
\lambda
#σ シグマ
\sigma
#φ ファイ
\phi
#ω オメガ
\omega
#他にもギリシア文字はあります。主なギリシア文字(大文字)
$$A, B,\Gamma,\Delta,\Pi,\Sigma,\Phi,\Psi,\Omega$$
#A アルファ
A
#B ベータ
B
#Γ ガンマ
\Gamma
#Δ デルタ
\Delta
#Π パイ
\Pi
#Σ シグマ
\Sigma
#Φ ファイ
\Phi
#Ψ プシー
\Psi
#Ω オメガ
\Omega
#他にもギリシア文字はあります。大小関係
$$< = > \leq \ge$$
#< = >
< = >
#≤
\leq
#≥
\ge大きなカッコ
$$(, \big( , \Big( , \bigg( , \Bigg(, \left( \frac{ 1}{2} \right)$$
#普通のカッコ(
(
#少し大きなカッコ
\big(
#大きなカッコ
\Big(
#かなり大きなカッコ
\bigg(
#とても大きなカッコ
\Bigg(
#中身に応じて変わるカッコ
\left( \frac{ 1}{2} \right)分数
$$\frac{a}{b}$$
#aを分子、bを分母とした分数
\frac{a}{b}上付き文字
$$x^2 x^{a+b}$$
#Xの右下に1文字だけつけるコード
X^2
#Xの右下に2文字以上つけるコード
X^{a+b}下付き文字
$$X_i X_{abcd}$$
#Xの右下に1文字だけつけるコード
X_i
#Xの右下に2文字以上つけるコード
X_{abcd}指数・対数
$$a^2 \log_{4}16=2 log_{4}16=2$$
#指数
a^2
#対数 ※\をつける
\log_{4}16=2
#\をつけないと上の右端になりますが、好まれません
log_{4}16=2Σ(シグマ)
$$\sum_{i=1}^n X_i$$
#i=1,2,3...nまでのXiを合計するシグマ
$\sum_{i=1}^n X_i
#Xの右下にiをつけるコード
X_i極限
$$e = \lim_{n \to \infty} (1 + \frac{1}{n} )^n$$
#自然対数の定義
e = \lim_{n \to \infty} (1 + \frac{1}{n})^n
#極限 ※\つける
\lim
#右矢印→
\to
#無限∞
\infty微分
$$f'(x) \frac{df}{dx}$$
#関数fをxで微分する
f'(x)
\frac{df}{dx}$$\frac{\partial f}{\partial x}$$
#関数fをxで偏微分
\frac{\partial f}{\partial x}
#ラウンドディー∂のコード
\partial積分
$$\int \int_{b}^{a} \int_{b}^{a} f(x) dx$$
#インテグラルの記号
\int
\int_{b}^{a}
#定積分
\int_{b}^{a} f(x) dx最適化
$$\max_{x} U(x) \min_{x,y} U(x,y)$$
#maxの下に文字をつける
\max_{X} U(X)
#minの下に文字をつける
\min_{x,y} U(x,y)
#最大、最小
\max \min特殊な表現
$$\cdots \left. \frac{du}{dx} \right |_{a=1} \bar{X} \overline{XYZ} \hat{a} \widehat{XY}$$
$$ \tilde{a} \widetilde{ab} \infty \Rightarrow \partial \mathcal{L} \mathbb{R}$$
#三点リーダー「・・・」
\cdots
#条件づけのための長い縦棒
\left. \frac{du}{dx} \right |_{a=1}
#↑解説「\left.」左「\right」|右です。
#バー
\bar{X}
\overline{XYZ}
#ハット^
\hat{a}
\widehat{XY}
#チルダ~
\tilde{a}
\widetilde{ab}
#∞
\infty
#⇒
\Rightarrow
#∂
\partial
#L
\mathcal{L}
#二重文字
\mathbb{R}
\doubleR #パワーポイントでの出力の場合