ラムゼイ・モデルでは、パレート最適な資源配分が実現する。パレート最適とは「誰かが損をすることなしに、誰かが得をすることない」という資源配分である。つまり、最適成長モデルがパレート最適な資源配分を実現するとは「鞍点経路と定常均衡の成長経路から外れて、消費を増やそうとしても、それ以降に消費が減ってしまう」を意味する。
ポイントは、今期の消費を増やせば、今期の貯蓄が減り、今期の投資が減り、次期の資本が減り、次期の生産力が減り、次期の消費が減るということだ。各期間で分解して考えてみよう。画像1より、鞍点経路はパレート最適である。なぜなら、1期に鞍点経路(赤)より多い消費(青)をすると、2期以降は鞍点経路より少ない消費になるからだ。画像2より、定常均衡はパレート最適である。なぜなら、T期に定常均衡(赤)より多い消費(青)をすると、少なくともT+1期は定常均衡より少ない消費になるからだ。
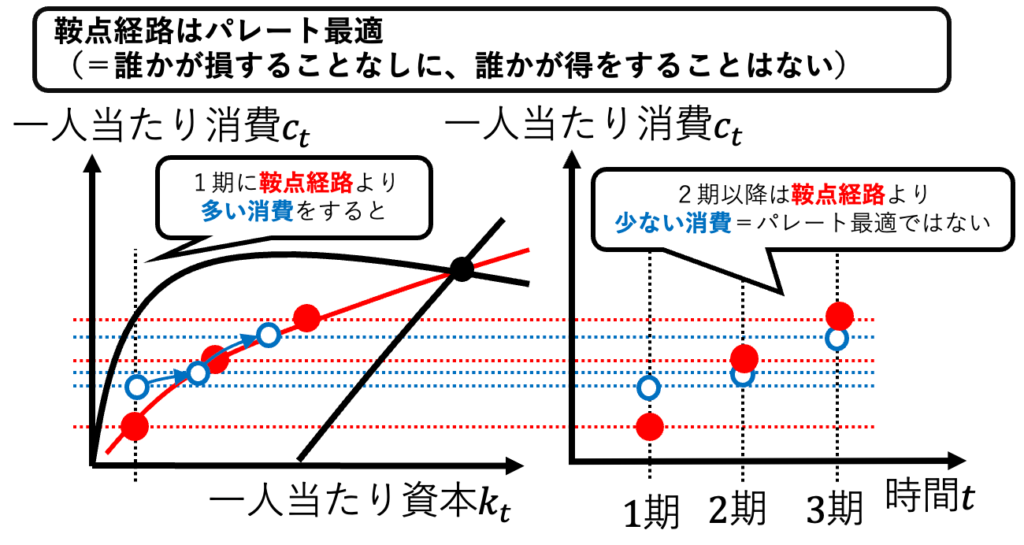
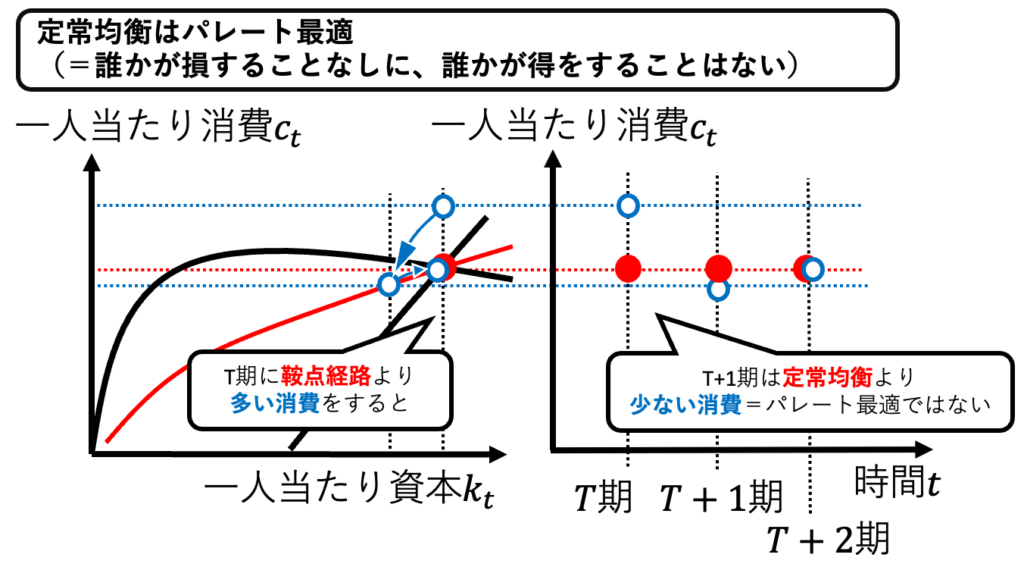
ラムゼイ・モデルがパレート最適を実現するとは、ソロー・モデルに市場メカニズムを導入すると最適な資源分配が実現するということである。
