技術進歩と人口成長のある最適成長モデルでも、経済状態は鞍点経路に沿って定常均衡に達して、一人当たりGDPは技術進歩率で成長する。したがって、ソロー・モデルに消費者と企業の合理的行動と市場メカニズムを導入しても、技術進歩こそが長期的な人類の生活水準を決めるという結論は変わらない。
技術進歩と人口成長のある最適成長モデルは実際に計算するととても大変なので、位相図だけ示そう。一応、計算に興味のある向けに問題と解答を追記したが、おすすめしない。さて、計算の重要なポイントは、技術係数Aと労働Lを掛け合わせた効率労働1単位という形に帰着させることで、技術進歩と人口成長の成長トレンドを除去(Detrend)して、技術進歩と人口成長もしない最適成長モデル(解説)に帰着させる点である。効率労働1単位当たりの消費と資本の成長は、画像1のように技術進歩と人口成長もしない最適成長モデルと同じである。これを一人当たり消費と資本の成長の位相図に直すと、画像2のようになる。
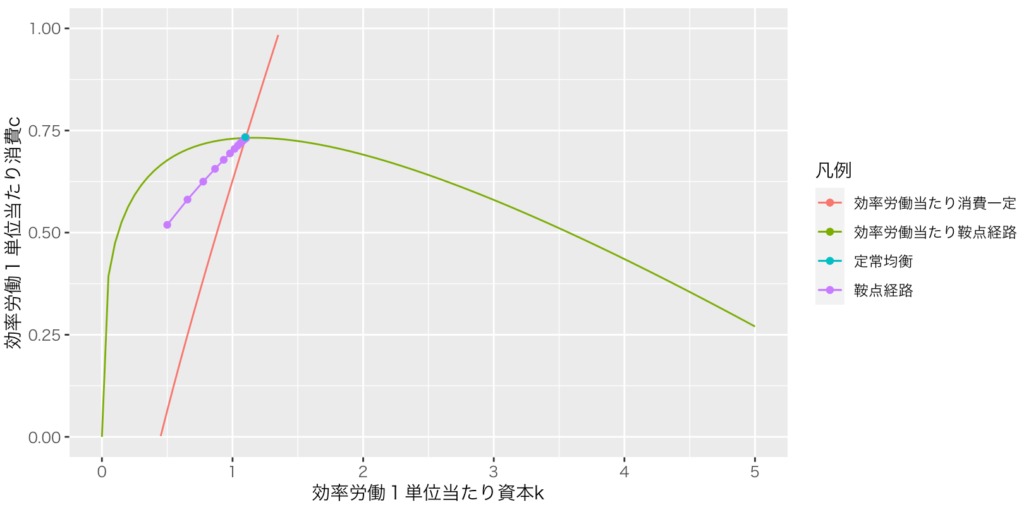
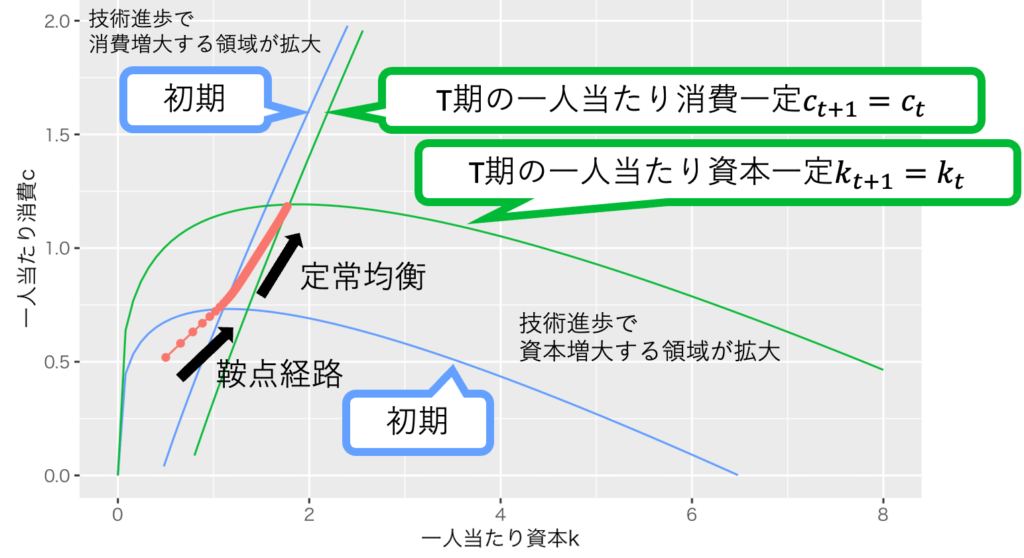
最適成長モデルの含意は「各期では、自由な市場経済に任せるとよい」「長期的には、技術進歩が生活水準を決める」である。前者は一般均衡理論と共通であり、後者はソロー・モデルと共通である。最適成長モデルは、動学的一般均衡モデル(DGE, Dynamic General Equilibrium)と呼ばれる。
【追記:問題】
注意:これ以降の問題を解くと、経済学が嫌いになるので、解かないでほしい。大事なのは、効率労働1単位当たりで考える、トレンド除去によって、人口成長ゼロ、技術進歩ゼロと同じような結果がもたらされるということである。
また、問題を解く際は次を用いよ。
・資本蓄積は次のように行われる。
$$次期の資本K_{t+1}=今期の資本K_{t}+今期の資本I_{t}-資本減耗\delta K_{t}$$
$$=K_{t}+今期の貯蓄[Asset]_{t}-\delta K_{t}$$
$$=K_{t}+(所得Y_t -消費C_t)-\delta K_{t}$$
$$=K_{t}+(総生産F(K_t,A_t L_t) -消費C_t)-\delta K_{t}$$
$$=F(K_t,A_t L_t) +(1-\delta) K_{t}-C_t$$
・技術係数Aと労働Lを掛け合わせた効率労働1単位当たりならば、小文字で表記する。
$$例:\frac{K_t}{A_t L_t}=k_t$$
・マクロ生産関数は次のように一次同次の性質をもつコブ=ダグラス型生産関数をする。
$$F(K_t,A_t L_t)=K_t^{\alpha} (A_t L_t)^{1-\alpha}$$
$$F(\frac{K_t}{A_t L_t},1)=f(k_t)=k_t^{\alpha}$$
・家計の効用最大化問題は、一人当たりで次のように定式化せよ。人口成長した際、資産は生きている人で平等に分配されるとする。
$$\max \sum_{t=0}^{\infty} \beta^t u \left( \frac{C_t}{L_t} \right)$$
$$s.t. \frac{C_t}{L_t}+\frac{[Asset]_t}{L_t}=(1+r_t)\frac{[Asset]_{t-1}}{L_t}+\frac{w_t L_t}{L_t}$$
・効用関数はCRRA型を仮定せよ。
$$CRRA型:u \left( \frac{C_t}{L_t} \right)=\frac{\left( \frac{C_t}{L_t} \right)^{1-\sigma}}{1-\sigma}$$
・企業は利潤最大化するので、次が成り立つ。ただし、利子率r、資本減耗率δ、賃金w。
$$\frac{\partial F(K_t,A_t L_t)}{\partial K_t}=r_t + \delta$$
$$\frac{\partial F(K_t,A_t L_t)}{\partial L_t}=w_t$$
・また、必要があれば、次を用いよ。
$$\frac{w_t}{A_t}= \widetilde{w_t}$$
$$\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right) $$
$$\widetilde{u(c_t)}=u \left( \frac{C_t}{A_t L_t} \right)$$
・労働L(=人口)と技術係数Aは次のように成長する。
$$A_{t+1}=(1+g)A_t,L_{t+1}=(1+n)L_t$$
問1:次の資本遷移式を効率労働1単位当たりに直せ。なお、集計変数は大文字、効率労働1単位当たりの変数は小文字で表記する。
問2:効率労働1単位当たりの資本が一定になる条件を導け。
問3:家計の効用最大化問題における制約条件式を効率労働1単位当たりに直せ。効率労働1単位当たりでは、小文字を用いよ。効率労働1単位当たりの賃金は「~w」とせよ。
$$\frac{w_t}{A_t}= \widetilde{w_t}$$
問4:家計の効用最大化問題における最大化式を効率労働1単位当たりに直せ。効率労働1単位当たりでは、小文字を用いよ。これはCRRA型効用関数の仮定が効いてくるのだが、効率労働1単位当たりの効用関数は「~U」とせよ。
$$\widetilde{u(c_t)}=u \left( \frac{C_t}{A_t L_t} \right)$$
問5:家計の効用最大化問題からオイラー方程式を求めよ。利子率rは企業の利潤最大化を用いて、処理せよ。また、必要があれば、次を使え。
$$\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right) $$
問6:効率労働1単位の消費cが一定になる条件を求めよ。
問7:効率労働1単位の消費cと資本kが一定になる定常均衡を求めよ。ただし、求めるのは資本kだけでよい。なぜなら、第一に資本kが求められれば消費cは直ちに求められるからであり、第二に式が複雑になりすぎるからである。
問8:効率労働1単位当たりでの消費と資本の動学モデルを整理せよ。問9でRによるシミュレーションを行う。
問9:効率労働1単位当たりでの消費と資本を、位相図の中でシミュレーションせよ。次のパラーメーターと初期値を与える。なお、CRRA型効用関数でσ=1とは、ログ型効用関数と同じである。
・α=0.3、β= 0.99、σ=1、δ=0.25、n=0.01、g=0.01
・期間T=50
・初期値(k1,c1)=(0.5, 0.5190227102)
問10:1人当たりでの消費と資本を、位相図の中でシミュレーションせよ。一人当たり消費一定、一人当たり資本一定の曲線は、t=1とt=50のみ描け。パラーメーターと初期値は問9と同じ。
【追記:解答】
問1:次の資本遷移式を効率労働1単位当たりに直せ。なお、集計変数は大文字、効率労働1単位当たりの変数は小文字で表記する。
$$K_{t+1}=K_t+I_t-\delta K_t$$
$$K_{t+1}=(1- \delta )K_t+(Y_t-C_t)$$
$$K_{t+1}=(1- \delta )K_t+F(K_t,A_t L_t)-C_t$$
$$\frac{K_{t+1}}{A_t L_t}=(1- \delta ) \frac{K_t}{A_t L_t}+\frac{1}{A_t L_t}F(K_t,A_t L_t)-\frac{C_t}{A_t L_t}$$
$$\frac{K_{t+1}}{A_t L_t}\frac{A_{t+1} L_{t+1}}{A_{t+1} L_{t+1}}=(1- \delta ) k_t+F \left( \frac{K_t}{A_t L_t},\frac{A_t L_t}{A_t L_t} \right)-c_t 一次同次より$$
$$k_{1+1}(1+g)(1+n)=(1- \delta ) k_t+f(k_t)-c_t・・・式1$$
$$k_{1+1}=\frac{f(k_t)+(1- \delta ) k_t-c_t}{(1+g)(1+n)}$$
$$これが資本蓄積の動学方程式である。$$
問2:効率労働1単位当たりの資本が一定になる条件を導け。
$$一人当たりの資本一定k_t=k_{t+1}を式1に代入して$$
$$k_{t}(1+g)(1+n)=(1- \delta ) k_t+f(k_t)-c_t$$
$$c_t=f(k_t)-(\delta+n +g +gn)k_{t}$$
問3:家計の効用最大化問題における制約条件式を効率労働1単位当たりに直せ。効率労働1単位当たりでは、小文字を用いよ。効率労働1単位当たりの賃金は「~w」とせよ。
$$\frac{w_t}{A_t}= \widetilde{w_t}$$
$$\frac{C_t}{L_t}=\frac{A_t C_t}{A_t L_t}=A_t c_tと$$
$$\frac{[Asset]_t}{L_t}=\frac{[Asset]_t}{A_t L_t}=[asset]_tより$$
$$\frac{C_t}{L_t}+\frac{[Asset]_t}{L_t}=(1+r_t)\frac{[Asset]_{t-1}}{L_{t}}\frac{L_{t-1}}{L_{t-1}}+\frac{w_t L_t}{L_t}$$
$$\frac{C_t}{L_t}+\frac{[Asset]_t}{L_t}=(1+r_t)\frac{[Asset]_{t-1}}{L_{t-1}}\frac{L_{t-1}}{L_{t}}+\frac{w_t L_t}{L_t}$$
$$\frac{C_t}{L_t}+\frac{[Asset]_t}{L_t}=\frac{1+r_t}{1+n}\frac{[Asset]_{t-1}}{L_{t-1}}+\frac{w_t L_t}{L_t}$$
$$A_t c_t+A_t [asset]_t=\frac{1+r_t}{1+n}A_{t-1} [asset]_{t-1}+w_t$$
$$c_t+[asset]_t=\frac{1+r_t}{(1+n)(1+g)} [asset]_{t-1}+\widetilde{w_t} なぜなら両辺A_tで割った$$
問4:家計の効用最大化問題における最大化式を効率労働1単位当たりに直せ。効率労働1単位当たりでは、小文字を用いよ。これはCRRA型効用関数の仮定が効いてくるのだが、効率労働1単位当たりの効用関数は「~U」とせよ。
$$\widetilde{u(c_t)}=u \left( \frac{C_t}{A_t L_t} \right)$$
$$u \left( \frac{C_t}{L_t} \right)=\frac{\left( \frac{C_t}{L_t} \right)^{1-\sigma}}{1-\sigma}$$
$$=\frac{\left( A_t c_t \right)^{1-\sigma}}{1-\sigma}$$
$$=\frac{\left( (1+g)^t A_0 c_t \right)^{1-\sigma}}{1-\sigma} なぜならA_{t+1}=(1+g)A_t$$
$$=A_0^{1-\sigma} ((1+g)^{1-\sigma})^t \frac{ c_t^{1-\sigma}}{1-\sigma}$$
$$したがって$$
$$\max \sum_{t=0}^{\infty} \beta^t A_0^{1-\sigma} ((1+g)^{1-\sigma})^t \frac{ c_t^{1-\sigma}}{1-\sigma}$$
$$=A_0^{1-\sigma} \sum_{t=0}^{\infty} \left( \beta \left( (1+g)^{1-\sigma} \right) \right)^t \frac{ c_t^{1-\sigma}}{1-\sigma}$$
$$\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right) とすると、最大化問題は$$
$$\max \sum_{t=0}^{\infty} \widetilde{\beta}^t \frac{ c_t^{1-\sigma}}{1-\sigma}$$
$$ここで\widetilde{u(c_t)}=u \left( \frac{C_t}{A_t L_t} \right) =\frac{\left( \frac{C_t}{A_t L_t} \right)^{1-\sigma}}{1-\sigma}=\frac{c_t^{1-\sigma}}{1-\sigma}より$$
$$\max \sum_{t=0}^{\infty} \widetilde{\beta}^t \widetilde{u(c_t)}と書き換えられる。$$
問5:家計の効用最大化問題からオイラー方程式を求めよ。利子率rは企業の利潤最大化を用いて、処理せよ。
$$\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right) とすると$$
$$\max \sum_{t=0}^{\infty} \widetilde{\beta}^t \widetilde{u(c_t)}$$
$$s.t. c_t+[asset]_t=\frac{1+r_t}{(1+n)(1+g)} [asset]_{t-1}+\widetilde{w_t}$$
$$ここでラグランジュの未定乗数法を用いる。$$
$$L=\sum_{t=0}^{\infty} \widetilde{\beta}^t \widetilde{u(c_t)}+\sum_{t=0}^{\infty} \lambda_t \left( \frac{1+r_t}{(1+n)(1+g)} [asset]_{t-1}+\widetilde{w_t} – c_t-[asset]_{t} \right) $$
$$ラグランジュ関数をc_tと[asset_t]で微分すればゼロなので$$
$$\frac{\partial L}{\partial c_t}=\beta^t \widetilde{u'(c_t)}-\lambda_t =0$$
$$\frac{\partial L}{\partial [asset]_t}=\lambda_{t+1} \frac{1+r_{t+1}}{(1+n)(1+g)}-\lambda_{t} =0$$
$$よって \widetilde{u'(c_t)}=\frac{1+r_{t+1}}{(1+n)(1+g)} \widetilde{u'(c_{t+1})}$$
$$さらに企業の利潤最大化f'(k_t)=r_t + \deltaより$$
$$よって \widetilde{u'(c_t)}=\widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} \widetilde{u'(c_{t+1})}$$
$$つまり、技術進歩や人口成長しない最適成長モデルとほぼ同じにできた。$$
$$技術進歩や人口成長のトレンド除去detrendができたと言える。$$
$$CRRA型の効用関数\widetilde{u(c_t)}=\frac{c_t^{1-\sigma}}{1-\sigma}より$$
$$\frac{1}{c_{t}^\sigma} =\widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} \frac{1}{c_{t+1}^\sigma} $$
$$c_{t+1}^{\sigma} =\widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} c_{t}^{\sigma} $$
$$c_{t+1}= \left( \widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} \right) ^{\frac{1}{\sigma}}c_{t} $$
問6:効率労働1単位の消費cが一定になる条件を求めよ。
$$c_{t+1}=c_tより$$
$$1=\left( \widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} \right) ^{\frac{1}{\sigma}}$$
$$1= \widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)}$$
$$1=\widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)}$$
$$ここでf(k_t)=k_t^{\alpha}よりf'(k_{t+1})=\alpha k_{t+1}^{\alpha -1 }$$
$$資本の動学方程式k_{1+1}=\frac{f(k_t)+(1- \delta ) k_t-c_t}{(1+g)(1+n)}より$$
$$f'(k_{t+1})=\alpha \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }$$
$$したがって、効率労働1単位の消費cが一定になる条件は$$
$$1=\widetilde{\beta} \frac{1+\alpha \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }-\delta}{(1+n)(1+g)}$$
問7:効率労働1単位の消費cと資本kが一定になる定常均衡を求めよ。ただし、求めるのは資本kだけでよい。なぜなら、第一に資本kが求められれば消費cは直ちに求められるからであり、第二に式が複雑になりすぎるからである。
$$【効率労働1単位の資本kが一定になる条件】$$
$$c_t=k_t^{\alpha}-(\delta+n +g +gn)k_{t}$$
$$【効率労働1単位の消費cが一定になる条件】$$
$$1= \frac{1+\alpha \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }-\delta}{(1+n)(1+g)}$$
$$これを連立して$$
$$1=\widetilde{\beta} \frac{1+\alpha \left( \frac{ (1+g+n+ng)k_t}{(1+g)(1+n)} \right) ^{\alpha -1 }-\delta}{(1+n)(1+g)}$$
$$1=\widetilde{\beta} \frac{1+\alpha k_t ^{\alpha -1 }-\delta}{(1+n)(1+g)}$$
$$(1+n)(1+g)=\widetilde{\beta} +\widetilde{\beta} \alpha k_t ^{\alpha -1 }-\widetilde{\beta}\delta$$
$$(1+n)(1+g)-\widetilde{\beta}+\widetilde{\beta}\delta=\widetilde{\beta} \alpha k_t ^{\alpha -1 }$$
$$k_t ^{\alpha -1 }=\frac{(1+n)(1+g)-\widetilde{\beta}+\widetilde{\beta}\delta}{\widetilde{\beta} \alpha}$$
$$k_t=\left( \frac{(1+n)(1+g)-\widetilde{\beta}+\widetilde{\beta}\delta}{\widetilde{\beta} \alpha} \right) ^{\frac{1}{\alpha -1}}$$
$$さて\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right) より$$
$$ k_t=\left( \frac{1-\beta \left( (1+g)^{1-\sigma} \right)+ \beta \left( (1+g)^{1-\sigma} \right) \delta}{\alpha \beta \left( (1+g)^{1-\sigma} \right)} \right)^{\frac{1}{\alpha – 1}}$$
$$ちなみに、これに人口成長n=0、技術進歩g=0、σ=0を代入すると↓となる。$$
$$ k_t=\left( \frac{1-\beta + \beta \delta}{\alpha \beta} \right)^{\frac{1}{\alpha – 1}}$$
$$なお「資本kが求められれば消費cは直ちに求められる」とは定常均衡における消費は$$
$$c_t=k_t^{\alpha}-(\delta+n +g +gn)k_{t}$$
$$であるので、k_tを上に代入すれば求められるからである。$$
問8:効率労働1単位当たりでの消費と資本の動学モデルを整理せよ。問9でRによるシミュレーションを行う。
$$\widetilde{\beta}=\beta \left( (1+g)^{1-\sigma} \right)とする。$$
$$【資本蓄積の動学方程式】$$
$$k_{1+1}=\frac{f(k_t)+(1- \delta ) k_t-c_t}{(1+g)(1+n)}$$
$$【オイラー方程式】$$
$$c_{t+1}= \left( \widetilde{\beta} \frac{1+f'(k_{t+1})-\delta}{(1+n)(1+g)} \right) ^{\frac{1}{\sigma}}c_{t} $$
$$c_{t+1}= \left( \widetilde{\beta} \frac{1+\alpha k_{t+1}^{\alpha-1}-\delta}{(1+n)(1+g)} \right) ^{\frac{1}{\sigma}}c_{t} $$
$$【資本一定】$$
$$c_t=f(k_t)-(\delta+n +g +gn)k_{t}$$
$$【消費一定】$$
$$1=\widetilde{\beta} \frac{1+\alpha \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }-\delta}{(1+n)(1+g)}$$
$$\frac{(1+n)(1+g)}{\widetilde{\beta}}=1+\alpha \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }-\delta$$
$$\frac{(1+n)(1+g)-1+\delta}{\alpha \widetilde{\beta}}= \left( \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)} \right) ^{\alpha -1 }$$
$$\left( \frac{(1+n)(1+g)-1+\delta}{\alpha \widetilde{\beta}} \right) ^{\frac{1}{\alpha -1} }= \frac{ k_t^{\alpha}+(1- \delta ) k_t-c_t}{(1+g)(1+n)}$$
$$\frac{1}{(1+g)(1+n)} \left( \frac{(1+n)(1+g)-1+\delta}{\alpha \widetilde{\beta}} \right) ^{\frac{1}{\alpha -1} }= k_t^{\alpha}+(1- \delta ) k_t-c_t$$
$$c_t= k_t^{\alpha}+(1- \delta ) k_t -\frac{1}{(1+g)(1+n)} \left( \frac{(1+n)(1+g)-1+\delta}{\alpha \widetilde{\beta}} \right) ^{\frac{1}{\alpha -1} }$$
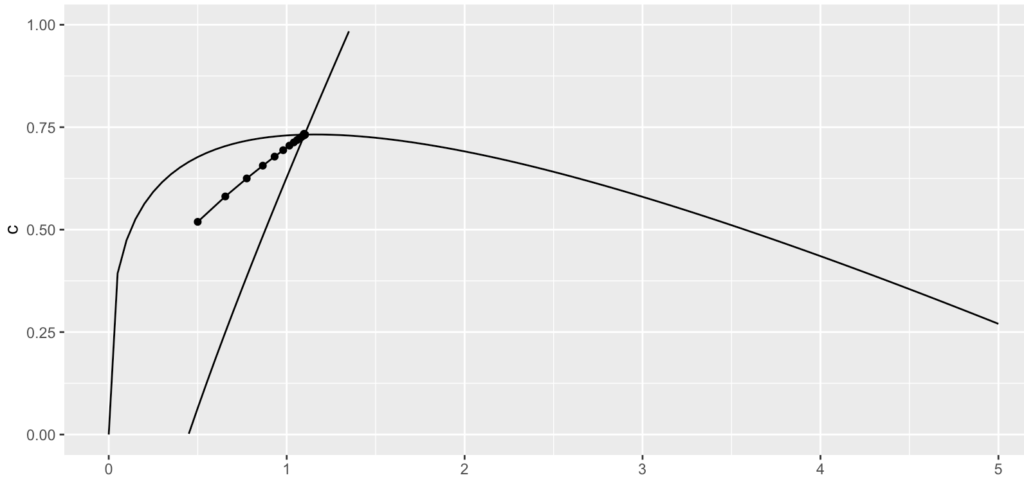
問9:効率労働1単位当たりでの消費と資本を、位相図の中でシミュレーションせよ。次のパラーメーターと初期値を与える。なお、CRRA型効用関数でσ=1とは、ログ型効用関数と同じである。
・α=0.3、β= 0.99、σ=1、δ=0.25、n=0.01、g=0.01
・期間T=50
・初期値(k1,c1)=(0.5, 0.5190227102)
#変数説明
#k=一人当たり資本、c=一人当たり消費
#行列準備
T <- 50 #シミュレーション期間
Data<- data.frame(matrix(0,T,3))
colnames(Data) <- c("time","k","c")
#初期値
Data[1,"time"] <- 1
Data[1,"k"] <- 0.5
Data[1,"c"] <- 0.5190227102
#パラメーター
a <- 0.3 #資本分配率α
bb <- 0.99 #本来の割引因子β
sg <- 1 #相対的リスク回避度
d <- 0.25 #資本減耗率δ
n <- 0.01 #人口成長率
g <- 0.01 #技術進歩率
b <- b*((1+g)^(1-sg)) #トレンド除去割引因子β
#資本蓄積の動学方程式
k_dynamicK <- function(k,c,a,d,g,n) {
nextK <- ((1-d)*k +k^a -c)/((1+g)*(1+n))
return(nextK)
}
#オイラー方程式
c_dynamicK <- function(nextK,c,a,b,d,g,n) {
nextC <- c*((b*(1+a*nextK^(a-1)-d)/((1+n)*(1+g)))^(1/sg))
return(nextC)
}
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1)){
Data[t+1,"time"] <- 1 + Data[t,"time"]
k <- Data[t,"k"]
c <- Data[t,"c"]
nextK <- k_dynamicK(k,c,a,d,g,n)
nextC <- c_dynamicK(nextK,c,a,b,d,g,n)
Data[t+1,"k"] <- nextK
Data[t+1,"c"] <- nextC
}
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#消費一定の消費
c_constantC <- function(k,a,b,d,n,g) {
A <- (((1+n)*(1+g)-1+d)/(a*b))^(1/(a-1))
c <- k^a + (1-d)*k - (A/((1+n)*(1+g)))
return(c)
}
c_constantC_graph<- function(k) {
c <- c_constantC(k,a,b,d,n,g)
return(c)
}
#資本一定の消費
c_constantK <- function(k,a,d,n,g) {
c <- k^a - (d+n+g+g*n)*k
return(c)
}
c_constantK_graph<- function(k) {
c <- c_constantK(k,a,d,n,g)
return(c)
}
#シンプル
ggplot()+
geom_path(data=Data,aes(x = k, y = c))+
geom_point(data=Data,aes(x = k, y = c))+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X),fun = c_constantC_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X),fun = c_constantK_graph)+
scale_x_continuous(limits=c(0,5))+
scale_y_continuous(limits=c(0,1))
#本文の図作成
ggplot()+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "効率労働当たり消費一定"),fun = c_constantC_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "効率労働当たり鞍点経路"),fun = c_constantK_graph)+
geom_path(data=Data,aes(x = k, y = c,colour = "鞍点経路"))+
geom_point(data=Data,aes(x = k, y = c,colour = "鞍点経路"))+
geom_point(aes(x = Data[T,"k"], y = Data[T,"c"],colour = "定常均衡"))+
scale_x_continuous(limits=c(0,5))+
scale_y_continuous(limits=c(0,1))+
labs(color = "凡例")+
xlab("効率労働1単位当たり資本k") +
ylab ("効率労働1単位当たり消費c") +
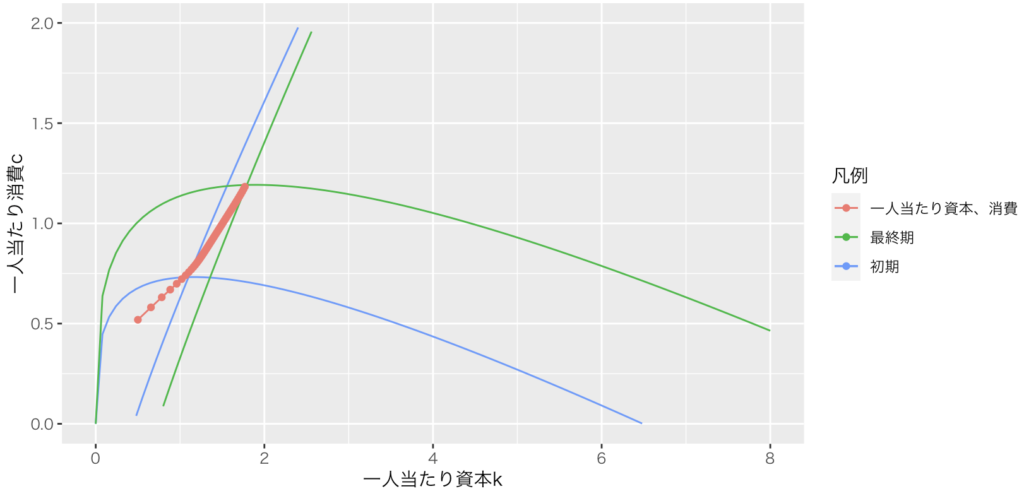
theme_grey(base_family = "HiraKakuPro-W3")問10:1人当たりでの消費と資本を、位相図の中でシミュレーションせよ。一人当たり消費一定、一人当たり資本一定の曲線は、t=1とt=50のみ描け。パラーメーターと初期値は問10と同じ。
#変数説明
#k=一人当たり資本、c=一人当たり消費
#行列準備
T <- 50 #シミュレーション期間
Data<- data.frame(matrix(0,T,6))
colnames(Data) <- c("time","A","k","c","kk","cc")
#初期値
Data[1,"time"] <- 1
Data[1,"A"] <- 1
Data[1,"k"] <- 0.5
Data[1,"c"] <- 0.5190227102
Data[1,"kk"] <- Data[1,"k"]*Data[1,"A"]
Data[1,"cc"] <- Data[1,"c"]*Data[1,"A"]
#パラメーター
a <- 0.3 #資本分配率α
bb <- 0.99 #本来の割引因子β
sg <- 1 #相対的リスク回避度
d <- 0.25 #資本減耗率δ
n <- 0.01 #人口成長率
g <- 0.01 #技術進歩率
b <- b*((1+g)^(1-sg)) #トレンド除去割引因子β
#資本蓄積の動学方程式
k_dynamicK <- function(k,c,a,d,g,n) {
nextK <- ((1-d)*k +k^a -c)/((1+g)*(1+n))
return(nextK)
}
#オイラー方程式
c_dynamicK <- function(nextK,c,a,b,d,g,n) {
nextC <- c*((b*(1+a*nextK^(a-1)-d)/((1+n)*(1+g)))^(1/sg))
return(nextC)
}
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1)){
Data[t+1,"time"] <- 1 + Data[t,"time"]
Data[t+1,"A"] <- (1+g)*Data[t,"A"]
k <- Data[t,"k"]
c <- Data[t,"c"]
nextK <- k_dynamicK(k,c,a,d,g,n)
nextC <- c_dynamicK(nextK,c,a,b,d,g,n)
Data[t+1,"k"] <- nextK
Data[t+1,"c"] <- nextC
Data[t+1,"kk"] <- nextK*Data[t,"A"]
Data[t+1,"cc"] <- nextC*Data[t,"A"]
}
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#t=Tの時の技術係数
At <- Data[T,"A"]
#消費一定の消費(t=1)
c1_constantC <- function(k,a,b,d,n,g) {
A <- (((1+n)*(1+g)-1+d)/(a*b))^(1/(a-1))
c <- k^a + (1-d)*k - (A/((1+n)*(1+g)))
return(c)
}
c1_constantC_graph<- function(k) {
c <- c_constantC(k,a,b,d,n,g)
return(c)
}
#消費一定の消費(t=T)
cT_constantC <- function(k,a,b,d,n,g,At) {
A <- (((1+n)*(1+g)-1+d)/(a*b))^(1/(a-1))
cc <- (k/At)^a + (1-d)*(k/At) - (A/((1+n)*(1+g)))
c <- cc*At
return(c)
}
cT_constantC_graph<- function(k) {
c <- cT_constantC(k,a,b,d,n,g,At)
return(c)
}
#資本一定の消費(t=1)
c1_constantK <- function(k,a,d,n,g) {
c <- k^a - (d+n+g+g*n)*k
return(c)
}
c1_constantK_graph<- function(k) {
c <- c1_constantK(k,a,d,n,g)
return(c)
}
#資本一定の消費(t=T)
cT_constantK <- function(k,a,d,n,g,At) {
cc <- (k/At)^a - (d+n+g+g*n)*(k/At)
c <- cc*At
return(c)
}
cT_constantK_graph<- function(k) {
c <- cT_constantK(k,a,d,n,g,At)
return(c)
}
ggplot()+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "初期"),fun = c1_constantC_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "初期"),fun = c1_constantK_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "最終期"),fun = cT_constantC_graph)+
stat_function(data=data.frame(X=c(-1,4)), aes(x=X,colour = "最終期"),fun = cT_constantK_graph)+
geom_path(data=Data,aes(x = kk, y = cc,colour = "一人当たり資本、消費"))+
geom_point(data=Data,aes(x = kk, y = cc,colour = "一人当たり資本、消費"))+
scale_x_continuous(limits=c(0,8))+
scale_y_continuous(limits=c(0,2))+
labs(color = "凡例")+
xlab("一人当たり資本k") +
ylab ("一人当たり消費c") +
theme_grey(base_family = "HiraKakuPro-W3")