操作変数モデルにおいて回帰係数を推定する場合、2段階最小二乗推定量(2SLS:2 stage least squares)を使うことができる。母集団モデルについては「操作変数モデルについて」をご覧頂きたい。この記事では、その推定について扱う。XはUと相関する内生変数、WはUと相関しない外生変数である。
$$操作変数モデル Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k$$
$$+\beta_{k+1} W_{k+1} + \cdots + \beta_{k+p} W_{k+p}+U$$
2SLS推定では、2段階で回帰する。第①段階目は、内生変数Xを目的変数に、操作変数Zと外生変数Wを説明変数にした最小二乗推定を、すべての内生変数Xについて行う(①-1〜①-k)。これにより「内生変数X=予測値^X+残差」となる。内生変数Xの誤差項Uと相関している要素は残差に吸収されるので、内生変数Xの予測値^Xと誤差項Uは相関しない。第②段階目は、内生変数Xをその予測値^Xに置き換えた回帰式②で最小二乗推定を行う。②段階目で得られた推定値が、2SLS推定値となる。
$$①-1:X_1=\beta_{0,X_1}+\beta_{1,X_1}Z_1+\cdots + \beta_{m,X_1}Z_m+\beta_{m+1,X_1}W_1+\cdots +\beta_{m+p,X_1}W_p+誤差項$$
$$\cdots$$
$$①-k:X_k=\beta_{0,X_k}+\beta_{1,X_k}Z_1+\cdots + \beta_{m,X_k}Z_m+\beta_{m+1,X_k}W_1+\cdots +\beta_{m+p,X_k}W_p+誤差項$$
$$第①段階目で得られた予測値:\widehat{X_1},\widehat{X_2},\cdots,\widehat{X_k}$$
$$\widehat{X_1}=\widehat{\beta_{0,X_1}}+\widehat{\beta_{1,X_1}}Z_1+\cdots + \widehat{\beta_{m,X_1}}Z_m+\widehat{\beta_{m+1,X_1}}W_1+\cdots +\widehat{\beta_{m+p,X_1}}W_p$$
$$②段階目の回帰モデル:Y=\beta_0 +\beta_1 \widehat{X_1} + \cdots + \beta_k \widehat{X_k}+\beta_{k+1} W_{k+1} + \cdots + \beta_{k+p} W_{k+p}+誤差項$$
2SLS推定は、RのパッケージAERを用いて、次のコードで実行できる。内生変数Xは|の左側、外生変数Wは|の左右両方、操作変数は|の右側に書く。なお、操作変数の数≧外生変数の数という次数制約を守らないと計算できない。
library(AER)
ivreg(data = Data, Y ~ X1 + X2 +W1 + W2 | Z1 + Z1 + W1 + W2)
【追記】
最も単純な操作変数モデル(下図)で2SLS推定量を使うとは、次の計算を実行することである。
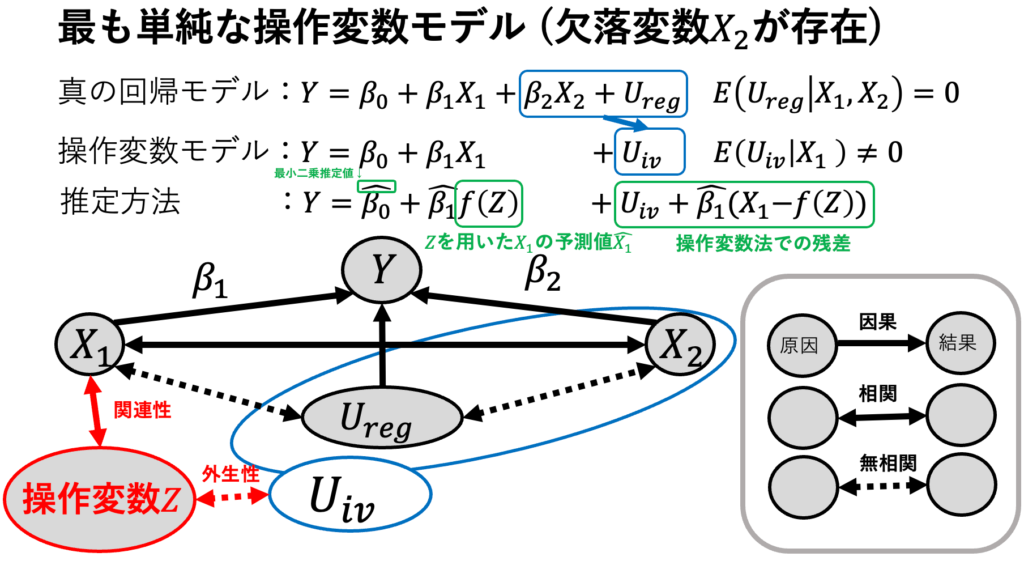
$$操作変数モデル Y=\beta_0 +\beta_1 X_1 +U$$
$$第一段階回帰:X_1=\beta_{0,X_1}+\beta_{1,X_1}Z+誤差項$$
$$一段階目で得られた予測値:\widehat{X_1}=f(Z)=\widehat{\beta_{0,X_1}}+\widehat{\beta_{1,X_1}}Z$$
$$二段階目の回帰:Y=\beta_0 +\beta_1 \widehat{X_1} +誤差項$$
に二段階目の回帰で得られた最小二乗法推定値が2SLS推定値になる。
