「中立的ですよ〜」と大人な顔しているくせに、的外れなことを言う人を見ると、腹が立つ。中立的であっても、実態を踏まえた意見を言ってほしい。これを踏まえた概念が統計学にはある。
効率性(efficiency)とは、不偏推定量の中で最も分散が小さいという推定量の性質である。例えば、図1の赤の推定量が頑健性のある推定量だ。図1には、求めたいパラメーターθが80と、赤の推定量、青の推定量、緑の推定量の分布が描かれている。3つの推定量は、どれも不偏性を持つ。ただし、その中で最も分散が小さいのが赤の推定量だ。これが効率性だ。
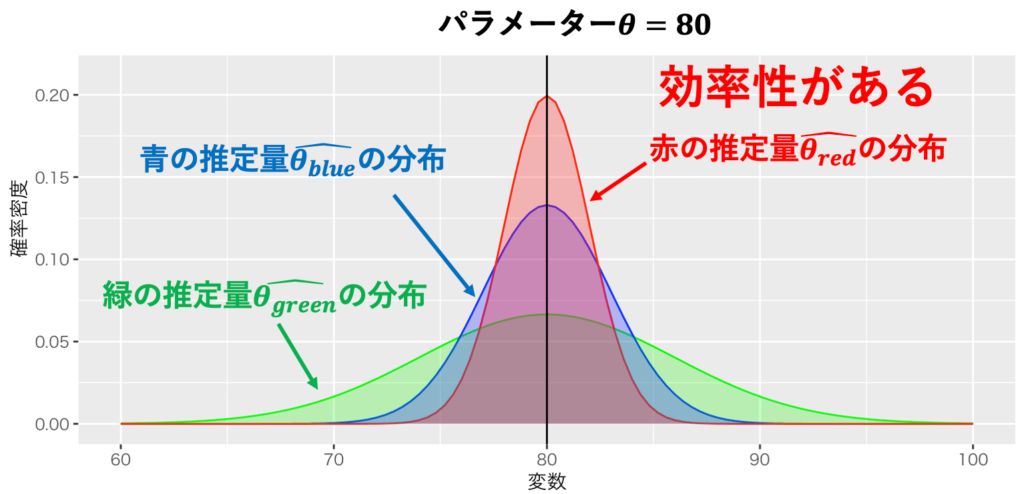
出典:しまうま総研(2023)
解説:コードは付録に掲載
しかし、実際のところ、不偏性があるだけで満足すべきで、効率性まで求めるのは求めすぎかもしれない。データ分析では効率性を推定量に求めるなんて、求めすぎだ。例えば、重回帰モデルにおいて最小二乗推定量が効率性を持つには「無作為抽出」「外生性(=誤差項の期待値が0、かつ、誤差項のXの条件つき期待値が0)」「誤差項が均一分散」「誤差項が自己相関してない」が必要なことが知られている(ガウス=マルコフの定理)。観測データを使うなら、これらすべての条件が怪しい。まず一致性、次に不偏性を満たすことから始めよう。
【追記】
図1は、次のRコードで作図できる。
library(ggplot2)
ggplot(data = data.frame(X = c(60, 100)), aes(x = X))+
stat_function(fun = dnorm, args = list(mean = 80,sd = 6), color="green")+
stat_function(fun = dnorm, args = list(mean = 80,sd = 3), color="blue")+
stat_function(fun = dnorm, args = list(mean = 80,sd = 2), color="red")+
scale_y_continuous(limits=c(0,0.25))+
xlab("変数")+
ylab("確率密度")+
geom_ribbon(data=data.frame(X=x<-seq(60,100,len=101), Y=dnorm(x,mean=80,sd=6)), aes(x=X, ymin=0, ymax=Y),fill="green",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(60,100,len=101), Y=dnorm(x,mean=80,sd=3)), aes(x=X, ymin=0, ymax=Y),fill="blue",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(60,100,len=101), Y=dnorm(x,mean=80,sd=2)), aes(x=X, ymin=0, ymax=Y),fill="red",alpha=0.3)+
theme_grey(base_family = "HiraKakuPro-W3")+
geom_vline(xintercept =80 )