回帰不連続デザイン(RDD:Regression Discontinuity Design)は、ある閾値を超えたか超えないかだけで介入の有無が決まる場合、閾値近傍では「ほぼ同じ状況」かつ「介入の有無のみが異なる」という実験がデザインされたと解釈するモデルである。回帰不連続デザインは、次のモデルで表せる。Yが目的変数、Dが介入有ダミーである。ここでのXは説明変数ではなく、ランニング変数(running variable)である。また、介入の有無は、Xが閾値(cutoff)を超えるか超えないかで決定される。
$$Y=\beta_{e} D_{介入有ダミー} +f(X)$$
$$f(X)=\beta_0+\beta_1 X+\beta_2 X^2+\beta_3 X^3+ \cdots +U$$
βeは、閾値近傍での局所的な平均処置効果(LATE:local average treatment effect on the cutoff)と解釈できる(参考:ルービンの因果モデル)。なぜなら、次の通りである。また、図1は回帰不連続デザインができるように標本を乱数生成したものである。
$$LATE=E \left[ Y_{介入あり}|閾値近傍 \right]-E \left[ Y_{介入なし}|閾値近傍\right]$$
$$=E \left[ \beta_{e} +f(X)|閾値近傍 \right] -E \left[ f(X)|閾値近傍 \right] =\beta_{e}$$
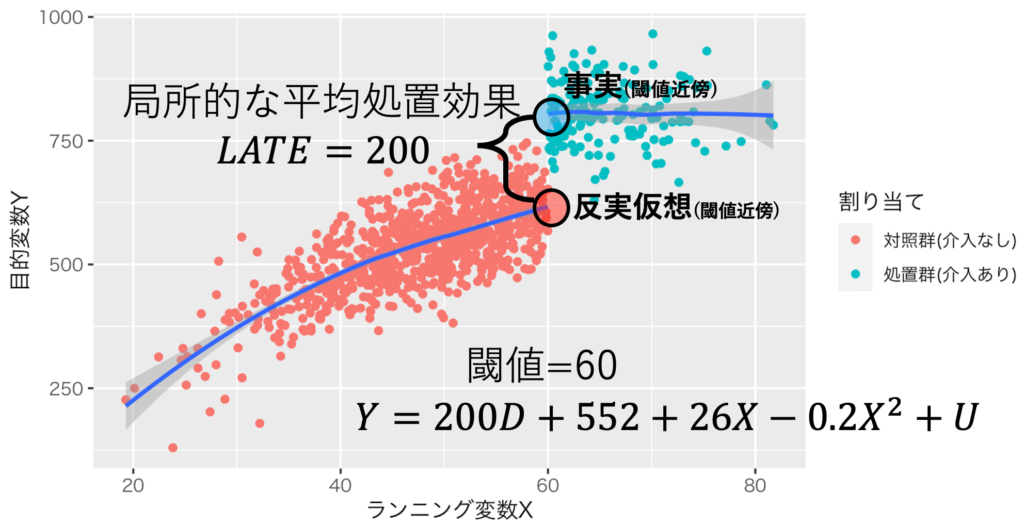
出典:しまうま総研(2023)が作成
補足:Rコードは追記に載せた。
ランニング変数と閾値があるのならば、回帰不連続デザインを使える。たしかに、閾値近傍では、介入の有無以外の他の条件は平均的には同じといえる(Ceteris paribus)。思いついた人は頭がいい。
【追記】
回帰不連続デザインには、連続性の仮定が必要だ。連続性の仮定とは、E[f(X)]は閾値近傍において連続という仮定である。この仮定が成り立たないと、介入のために非連続になったのか、元から不連続なのかが、識別できない。最も重要な仮定。
データの可視化では、RDプロットがよく使われる。図1は散布図に近似曲線を引いただけで、RDプロットではない。RDプロットとは、散布図を上下方向に細長いいくつもの長方形で切り分けて、その長方形に入るデータのYの平均値をプロットしたものである。

出典:しまうま総研(2023)が作成
補足:Rコードは追記に載せた。
回帰不連続デザインでの分析は、Rではパッケージrdrobustを用いてできる。
library(rdrobust) #呼び出し
rdplot(y,x,c =閾値) #RDプロット
Model <- rdrobust(y,x,c =閾値 , h=NULL) #RDDでの推定。hはバンド幅
summary(Model) #サマリー図1の描画、シミュレーション、推定に使ったRコードは以下の通り。
#パッケージの呼び出し
library(ggplot2)
library(rdrobust)
#標本生成
sample_size <- 1000
x <- rnorm(sample_size, mean =50, sd = 10)
d <- rep(0,sample_size)
category <- rep(0,sample_size)
for(i in 1:sample_size){
d[i] <- ifelse(x[i]>60, 1,0)
category[i] <- ifelse(x[i]>60,"treatment","control")
}
u <- rnorm(sample_size, mean =0, sd = 60)
y <- 200*d + 600 + 2*(x-60) - 0.2*(x-60)^2 + u
Data <- data.frame(x,y,category)
#ggplot2でRDプロット
library(ggplot2)
ggplot(Data, aes(x=x, y=y,stat= category))+
geom_point(aes(colour=category))+
geom_smooth(se = TRUE)+
scale_color_hue(name = "割り当て", labels = c(treatment ="処置群(介入あり)",control = "対照群(介入なし)") ) +
xlab("ランニング変数X") +
ylab ("目的変数Y") +
theme_grey(base_family = "HiraKakuPro-W3")
#回帰不連続デザインでの分析と図2
library(rdrobust)
rdplot(y,x,c =60, h =NULL,x.label = "X", y.label = "Y") #RDプロット
Model <- rdrobust(y,x,c =60 , h=NULL) #RDDでの推定
summary(Model)