労働余暇選択問題は、労働供給の合理的行動の基礎となる。この記事では労働余暇選択問題をラグランジュの未定乗数法で解く。これは次のように定式化できる。Uが消費cと余暇lを入力すると効用が出力される効用関数、wは賃金、hは労働時間、lは労働以外のすべての時間である。24は時間全体の長さを意味する。1日が24時間であるから24としたが、定数であれば365でも1でもよい。
$$\max U(c,l)$$
$$s.t. c=wh, h+l=24$$
労働余暇選択問題は、ラグランジュの未定乗数法を用いて計算することができる。
$$制約条件はc=whとh+l=24の二つで$$
$$ラグランジュ関数Lを次のように設定する$$
$$L(c,h,l,\lambda_{1},\lambda_{2})$$
$$=U(c,l)+\lambda_{1}(wh-c)+\lambda_{2}(24-h-l)$$
$$c,h,l,\lambda_{1},\lambda_{2}についての偏微分が0なので$$
$$\frac{\partial L}{\partial c}=\frac{\partial U(c ,l)}{\partial c}- \lambda_1=0…式(1)$$
$$\frac{\partial L}{\partial l}=\frac{\partial U(c ,l)}{\partial l}- \lambda_2=0…式(2)$$
$$\frac{\partial L}{\partial h}=w\lambda_1 – \lambda_2=0…式(3)$$
$$式(1)式(2)を式(3)に代入すると$$
$$w \frac{\partial U(c ,l)}{\partial c} – \frac{\partial U(c ,l)}{\partial l}=0$$
$$ここで限界効用をMUと表現すると$$
$$w MU_{消費} – MU_{余暇}=0$$
$$\frac{MU_{余暇}}{MU_{消費}}=w$$
賃金とは、余暇を送ることで発生する機会費用である。上の最終的な結果を限界代替率=価格比と解釈し、消費1単位に必要な価格P2を1とするならば、余暇の価格P1=wである。なぜなら、働けば賃金wが儲かるからだ。
$$限界代替率MRS_{余暇,消費}=\frac{MU_{余暇}}{MU_{消費}}=\frac{w}{1}=価格比\frac{P_1}{P_2}$$
【追記】
・無差別曲線で労働余暇選択
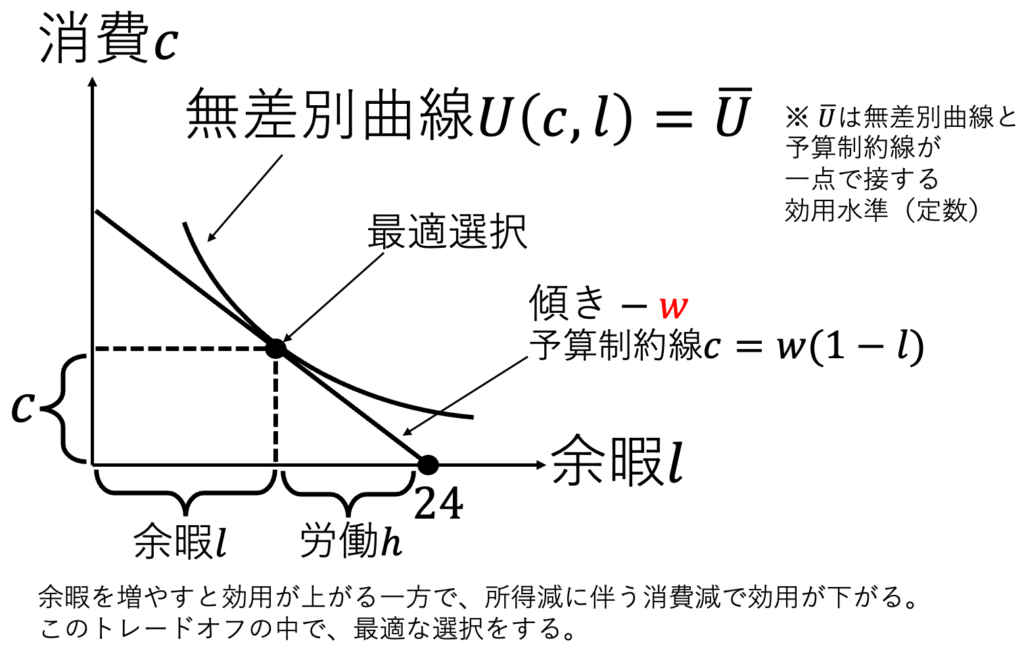
・賃金変化での代替効果、所得効果
賃金が上がると、基本的には余暇が少なくなり、より多く働くことになる。その程度は、代替効果と所得効果によって決定される。
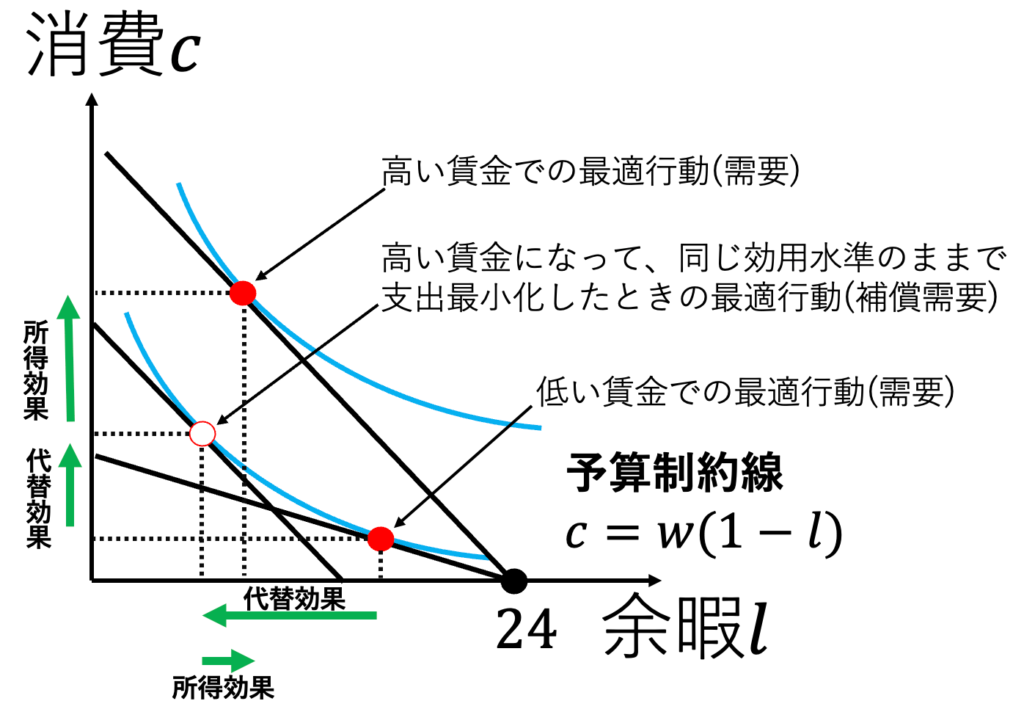
・労働供給曲線の後方屈曲性
労働供給は、賃金が上がりすぎるとむしろ働かなくなることが知られている。つまり、労働の供給曲線は、後ろに曲がる後方屈曲性を持つ場合がある。
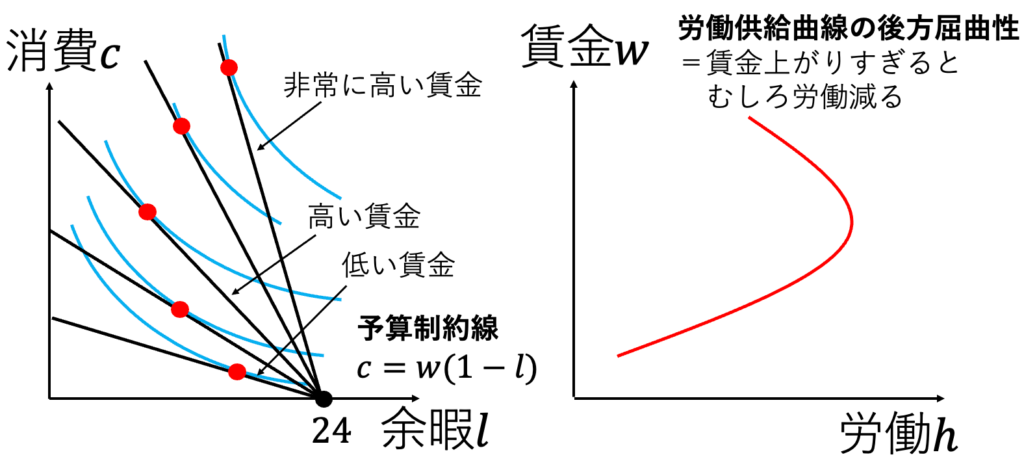
なぜ賃金が上がりすぎると、労働がむしろ減るのか。それは、余暇を減らして消費を増やす(代替)効果よりも、実質的な所得が増えたことで買える余暇が増える(所得)効果の方が、大きくなるからだ。
ただし、注意しなければならないのは、wが時給であることだ。年収(=時給w×1日労働時間h×年間労働日数)ではない。普通のサラリーマンにとって時給wが非常に高くなることは稀である。「時給が高すぎるのであんまり働かなくなる」ような後方屈曲している労働供給曲線に私自身が直面することはないだろう。
