技術進歩率は観測できないが、成長会計という手法を用いれば、技術進歩の経済成長への寄与度を計算できる。なお、成長会計では、次のコブ・ダグラス型マクロ生産関数を仮定している。
$$Y_t=F(K_t,L_t,E_t)=E K_t^ \alpha L_t^{1-\alpha}$$
$$E:全要素生産性TFP$$
$$E=A_t ^{1-\alpha}とみなせば、Y_t=K_t^ \alpha (A_t L_t)^{1-\alpha}$$
具体的には、技術進歩の寄与度は次のように計算できる。αは資本分配率である。なお、生産関数は非線形だが、寄与度が線形モデルで表されている。これは対数線形化という考え方である。テイラー展開の一次近似と関係する。
$$技術進歩の寄与度=経済成長率-資本蓄積の寄与度-人口成長の寄与度$$
$$=\log \left( \frac{Y_t}{Y_{t-1}} \right)-\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]-(1-\alpha)\left[ \log \left( \frac{L_t}{L_{t-1}} \right) \right]$$
$$≒経済成長率-\alpha(資本成長率)-(1-\alpha)(人口成長率)$$
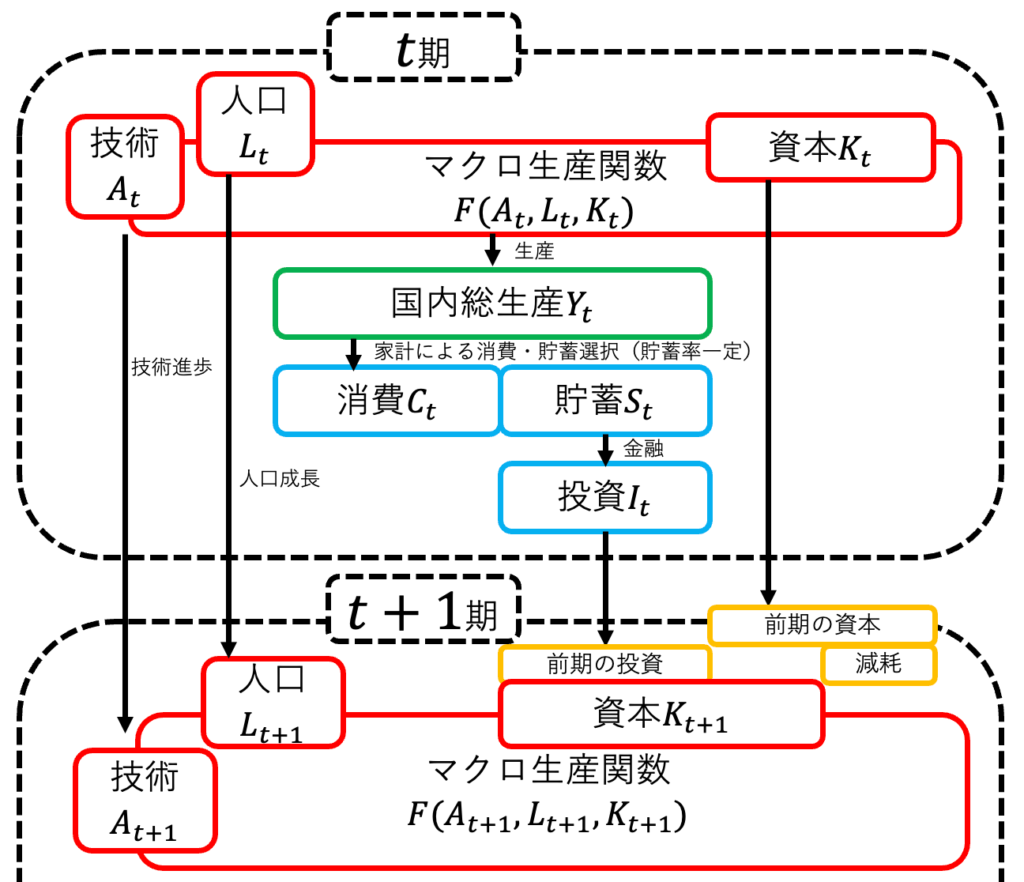
成長会計での「経済成長率は技術進歩率、人口成長率、資本蓄積に分解できる」と理論での「経済成長率は技術進歩率と人口成長率が決める」は矛盾しない。過程に注目すると、資本蓄積、人口増加、技術進歩の積み重ねで、経済成長している。これはソロー・モデルでもそうだ(画像1)。しかし、複雑な相互作用の結果で、経済成長は最終的に技術進歩率と人口成長率に帰着するのである。言わば、諸要素がいろいろ頑張った結果、定められた結果へ行き着くのだ。成長会計は過程、ソローモデルは結果に注目する。
【追記:問題】
問1:次のコブ・ダグラス型マクロ生産関数にて、正確な経済成長率を導け。
$$t期:Y_t=F(K_t,A_t L_t)=K_t^ \alpha (A_t L_t)^{1-\alpha}$$
問2:成長率が十分に0に近いとき、次の対数の性質が成り立つことを用いて、経済成長率の近似式を導け。
$$経済成長率=\frac{Y_t – Y_{t-1}}{Y_{t-1}}≒\log (Y_t)-\log (Y_{t-1})=\log \left( \frac{Y_t}{Y_{t-1}} \right)$$
問3:問2の式を経済成長の寄与度分解として解釈せよ。なお、寄与度分解とは下式のように成長率を、項目別に分解することである。
・経済成長率=資本蓄積の寄与度+技術進歩の寄与度+人口成長の寄与度
問4:技術進歩率は理論上の存在であり、観測することはできない。しかし、先ほどの式を用いて、技術進歩の寄与度を計算することはできる。それを示せ。なお、一次同次のコブダグラス型生産関数では、αは資本分配率を等しいことを用いてよい。
問5:技術進歩の寄与度は、技術進歩率ではない。技術進歩率gを、技術進歩の寄与度で表せ。次のソロー・モデルの結論と仮定を用いてよい。この結論は定常均衡についての記事の問2ー2で導出した。
$$定常均衡で\frac{Y_{t+1}}{Y_t}=(1+g)(1+n)$$
$$定常均衡で\frac{K_{t+1}}{K_t}=(1+g)(1+n)$$
$$定常均衡で\frac{L_{t+1}}{L_t}=1+n$$
問6:技術進歩の寄与度を「ソロー残差」と呼ぶ。高度成長期の日本のソロー残差は、現在の日本はソロー残差より大きい。問5までの文脈を考慮すると、この事実は何を意味するか?
問7:問5までの文脈を考慮しないと、低いソロー残差は他に何を意味しうるか?
【追記:解答】
問1:次のコブ・ダグラス型マクロ生産関数にて、正確な経済成長率を導け。
$$t期:Y_t=F(K_t,A_t L_t)=K_t^ \alpha (A_t L_t)^{1-\alpha}$$
$$t-1期:Y_{t-1}=F(K_{t-1},A_{t-1} L_{t-1})=K_{t-1}^ \alpha (A_{t-1} L_{t-1})^{1-\alpha}$$
$$よって経済成長率=\frac{Y_t – Y_{t-1}}{Y_{t-1}}=\frac{Y_t }{Y_{t-1}}-1$$
$$=\left( \frac{K_t}{K_{t-1}} \right)^ \alpha \left( \frac{A_t L_t}{A_{t-1} L_{t-1}} \right)^{1-\alpha}-1$$
問2:成長率が十分に0に近いとき、次の対数の性質が成り立つことを用いて、経済成長率の近似式を導け。
$$経済成長率=\frac{Y_t – Y_{t-1}}{Y_{t-1}}≒\log (Y_t)-\log (Y_{t-1})=\log \left( \frac{Y_t}{Y_{t-1}} \right)$$
$$経済成長率の近似=\log \left( \frac{Y_t}{Y_{t-1}} \right)$$
$$=\log \left[ \left( \frac{K_t}{K_{t-1}} \right)^ \alpha \left( \frac{A_t L_t}{A_{t-1} L_{t-1}} \right)^{1-\alpha} \right]$$
$$=\log \left[ \left( \frac{K_t}{K_{t-1}} \right)^ \alpha \right]+\left[ \log \left( \frac{A_t L_t}{A_{t-1} L_{t-1}} \right)^{1-\alpha} \right]$$
$$=\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]+(1-\alpha)\left[ \log \left( \frac{A_t L_t}{A_{t-1} L_{t-1}} \right) \right]$$
$$=\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]+(1-\alpha)\left[ \log \left( \frac{A_t }{A_{t-1} } \right) \right] + (1-\alpha)\left[ \log \left( \frac{L_t}{L_{t-1}} \right) \right]$$
問3:問2の式を経済成長の寄与度分解として解釈せよ。なお、寄与度分解とは下式のように成長率を、項目別に分解することである。
・経済成長率=資本蓄積の寄与度+技術進歩の寄与度+人口成長の寄与度
$$資本蓄積の寄与度=\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]$$
$$技術進歩の寄与度=(1-\alpha)\left[ \log \left( \frac{A_t }{A_{t-1} } \right) \right] $$
$$人口成長の寄与度=(1-\alpha)\left[ \log \left( \frac{L_t}{L_{t-1}} \right) \right]$$
問4:技術進歩率は理論上の存在であり、観測することはできない。しかし、先ほどの式を用いて、技術進歩の寄与度を計算することはできる。それを示せ。なお、一次同次のコブダグラス型生産関数では、αは資本分配率を等しいことを用いてよい。
$$技術進歩の寄与度=経済成長率-資本蓄積の寄与度-人口成長の寄与度$$
$$=\log \left( \frac{Y_t}{Y_{t-1}} \right)-\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]-(1-\alpha)\left[ \log \left( \frac{L_t}{L_{t-1}} \right) \right]$$
$$Y、L、K、\alphaは観測可能であり、技術進歩の寄与度を計算することはできる。$$
問5:技術進歩の寄与度は、技術進歩率ではない。技術進歩率gを、技術進歩の寄与度で表せ。次のソロー・モデルの結論と仮定を用いてよい。この結論は定常均衡についての記事の問2ー2で導出した。
$$定常均衡で\frac{Y_{t+1}}{Y_t}=(1+g)(1+n)$$
$$定常均衡で\frac{K_{t+1}}{K_t}=(1+g)(1+n)$$
$$定常均衡で\frac{L_{t+1}}{L_t}=1+n$$
$$ここで技術進歩の寄与度=\log \left( \frac{Y_t}{Y_{t-1}} \right)-\alpha \log \left[ \left( \frac{K_t}{K_{t-1}} \right) \right]-(1-\alpha)\left[ \log \left( \frac{L_t}{L_{t-1}} \right) \right]$$
$$=\log (1+g)(1+n)-\alpha \log (1+g)(1+n)-(1-\alpha) \log (1+n)$$
$$=\log (1+g)+\log(1+n)-\alpha \log (1+g)-\alpha \log (1+n)-(1-\alpha) \log (1+n)$$
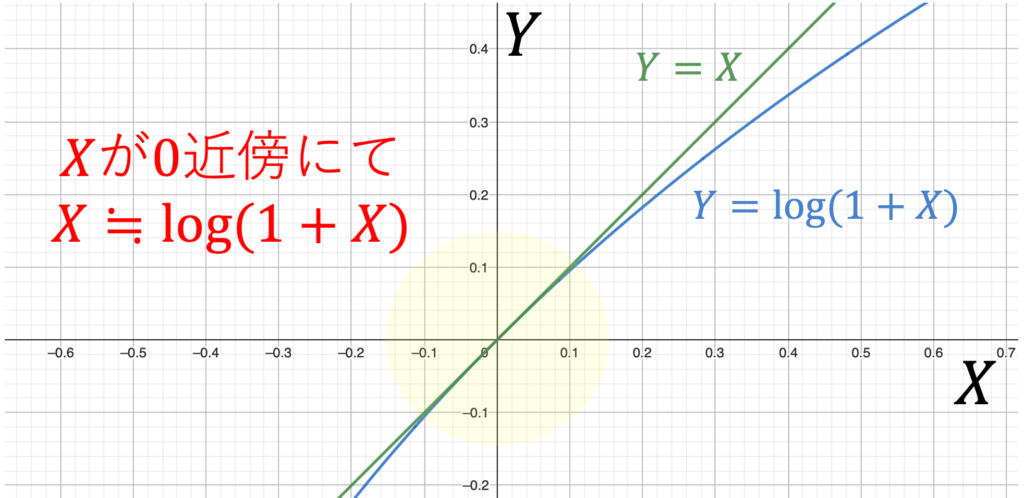
$$=(1-\alpha) \log (1+g)$$
$$≒(1-\alpha)g 下の画像を参照せよ$$
$$よって g=\frac{技術進歩の寄与度}{1-\alpha}$$
問6:技術進歩の寄与度を「ソロー残差」と呼ぶ。高度成長期の日本のソロー残差は、現在の日本はソロー残差より大きい。問5までの文脈を考慮すると、この事実は何を意味するか?
$$現在の日本は、高度経済成長期に比べて技術進歩が低迷している。$$
問7:問5までの文脈を考慮しないと、低いソロー残差は他に何を意味しうるか?
$$ソロー残差には人口成長、資本蓄積以外のすべての要素を含む。$$
$$したがって、技術進歩以外の要因も含まれる。$$
例えば、不景気、海外との競争激化、ゆとり教育や競争緩和で人材が低レベル化、雇用が不安定化による労働の熟練度低下、銀行や企業の不合理なまでのリスク回避傾向増大、起業家精神の低迷、労働文化の変容でモチベーション低下などが考えられる。
