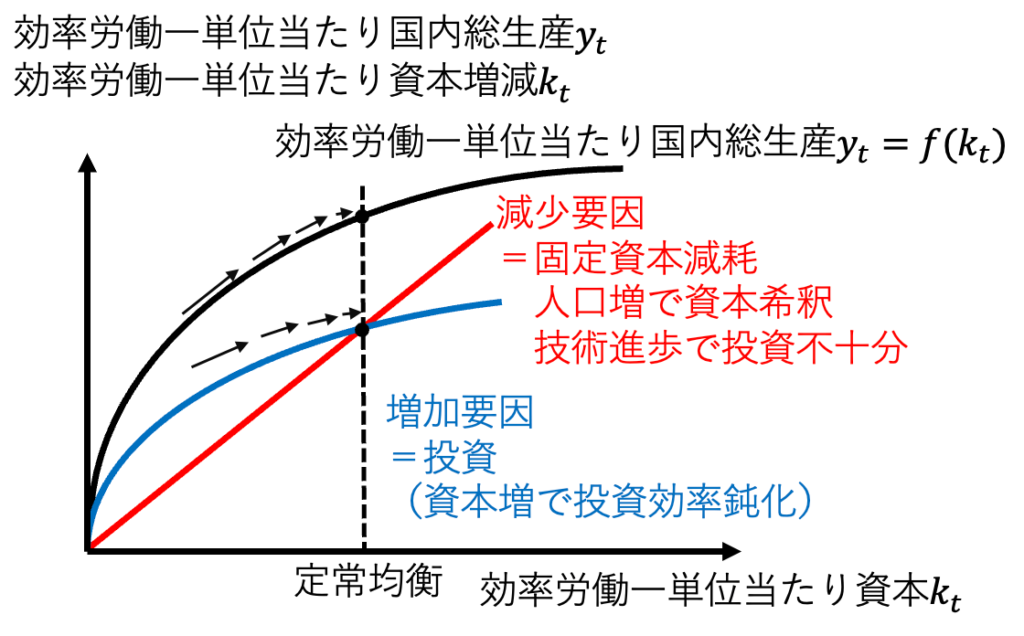
結論から申し上げれば、長期的な経済成長率は、一人当たりでは技術進歩、国全体では技術進歩と人口成長によって決まる。「ソロー成長モデル」を用いる。考えるポイントは、効率労働1単位当たり資本の増減である。効率労働とは、技術係数Aと労働Lを掛け合わせた疑似的な人間である。効率労働にとっての資本は、次の理由で増減する。そして、投資効率は資本蓄積が進むと下がっていくので、画像1のように効率労働1単位当たりの資本の増加はプラスからゼロになっていく。そして、定常均衡に至る。
$$増加要因:投資(資本少ないと投資効率高く、多いと鈍化)$$
$$減少要因その1:故障、摩耗、陳腐化といった資本減耗$$
$$減少要因その2:人口成長による1人あたりの資本不足$$
$$減少要因その3:技術進歩による技術あたりの資本不足$$
効率労働1単位当たりでの定常均衡は、一人当たりで換算すると、成長を続ける。具体的には「効率労働1単位当たりのGDPが一定」は「一人当たりGDPが技術進歩で成長する」「国のGDPが技術進歩と人口成長で成長する」を意味する。画像2は、パラメーターを適当においたソローモデルのシミュレーションである。効率労働一単位当たりでは定常均衡に到達するも、一人当たりでは持続的な成長が技術進歩によって達成されていることがわかる。
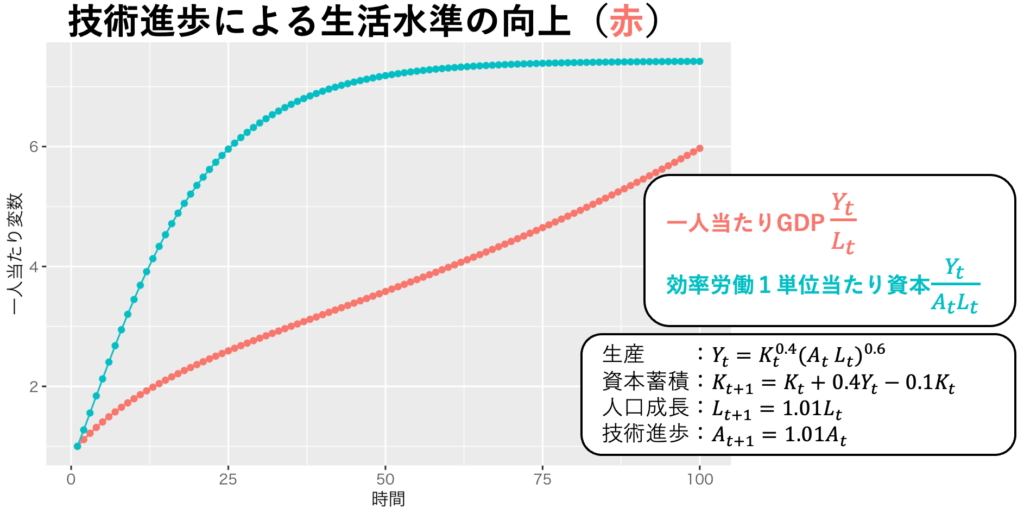
ソロー成長モデルの最も重要な示唆は「技術進歩が人類の幸せのために最も重要である」ということである。なぜなら、我々の生活水準は一人当たりGDPであり、一人当たりGDPは技術進歩によって成長するからだ。言い換えれば、長い目で見ると「社会全体のパイを増やす」のは技術進歩である。
【追記:モデルの詳細】
モデルの直感的な解説は「ソロー成長モデルについて」をみてほしい。
アルファベットの意味は「t:離散的な時間。自然数。time」「Y:国内総生産。Yield」「F:マクロ生産関数。Function」「K:資本。Kapital(ドイツ語)」「A:技術係数。Art」「L:労働(=人口)。Labor」「I:投資。Investment」「S:貯蓄。Saving」「g:技術進歩率。Growth」「n:人口成長率。Number」「δ:固定資本減耗率。fixed capital Depreciation rate)。また、モデルを解く際は「効率労働:AL」とし、効率労働一単位当たりの資本、生産関数などを小文字で表すことが多い。例えば、k=K/AL、f(k)=F(K/AL,1)。
$$【家計】$$
$$投資:S_t=sY_t$$
$$貯蓄率s一定を仮定:s_t=s$$
$$これはクズネッツ型消費関数$$
$$【企業】$$
$$国内総生産:Y_t=F(K_t,A_tL_t)$$
$$ただし、マクロ生産関数は次の3条件を満たす。$$
$$限界生産性は正:\frac{\partial Y}{\partial K}>0,\frac{\partial Y}{\partial L}>0$$
$$↑生産要素を増やせば生産量は必ず増える$$
$$限界生産性逓減:\frac{\partial^2 Y}{\partial K^2} <0,\frac{\partial^2 Y}{\partial L^2} <0$$
$$↑生産要素を増やせば、増える生産量は必ず減っていく$$
$$規模に対して収穫一定:F(\lambda K, \lambda AL)=\lambda F(K, AL)$$
$$↑資本Kと効率労働ALを2倍にしたら生産性変わらず生産量Yは2倍$$
$$↑数学的には1次同次という。$$
$$↑n次同次:F(\lambda K, \lambda AL)=\lambda^n F(K, AL)$$
$$【財市場均衡条件】$$
$$Y_t=C_t+I_t$$
$$生産面のGDP:Y_t$$
$$支出面のGDP:C_t+I_t$$
$$財供給F(K_t,A_t L_t)側が需要(C_t+I_t)を決定$$
$$なお、政府部門G_t、海外部門NX_tを無視$$
$$【金融市場均衡条件】$$
$$投資:S_t=I_t$$
$$資金供給S_t側が資金需要I_tを決定$$
$$I_t(r_t)と考え利潤最大化問題を解けば利子率r_tを得られる$$
$$【労働市場均衡条件】$$
$$労働:L_t^{供給}=L_t^{需要}$$
$$労働供給L_t^{供給}側が労働需要L_t^{需要}を決定$$
$$L_t^{需要}(w_t)と考え利潤最大化問題を解けば賃金w_tを得られる$$
$$【動学モデル】$$
$$資本遷移式:K_{t+1}=K_t+I_t-\delta K_t$$
$$=sF(K_t,A_tL_t)+(1-\delta)K_t$$
$$マルサス型の指数関数的人口成長L_{t+1}=(1+n)L_t$$
$$外生的な技術進歩:A_{t+1}=(1+g)A_t$$
$$【企業についての補足】$$
$$生産関数を特定化して考えたい場合は$$
$$F(K_t,A_tL_t)=K_t^\alpha (A_tL_t)^{1-\alpha}$$
$$0<\alpha<1。\alphaは資本分配率と解釈できる。$$
$$のコブ・ダグラス型を使って良い。これは上の3条件を満たす。$$
$$ただし、ソロー・モデルの結論は3条件が満たされる生産関数なら成り立つ。$$
【追記:問題】
問:技術係数A×労働Lを効率労働(effective labor)という疑似的な労働者とみなす。g>0、n>0を仮定し、効率労働1単位当たりの経済変数を小文字に表して、以下の問いに答えなさい。
問1:効率労働一単位当たり資本遷移式(後述)を書け。
$$k_{t+1}=・・・$$
$$ヒント:y_t=\frac{Y_t}{A_tL_t}, f(k)=F \left(\frac{K_t}{A_tL_t},1 \right)$$
問2:「効率労働一単位当たり資本の増加」「効率労働一単位当たり資本の減少」が一致する定常均衡において、「一人当たり」資本が毎期ごとに何倍になるのか答えなさい。
問3:定常均衡において、「一人当たり」GDPが毎期ごとに何倍になるのか答えなさい。
問4:定常均衡において、「国のGDP」が毎期ごとに何倍になるのか答えなさい。
問5:R言語を用いて「一人当たりGDP」についてのシミュレーションを実行せよ。ただし、以下のモデルを用いよ。
$$Y_t=F(K_t,A_t L_t)=K_t^\alpha (A_t L_t)^{1-\alpha}$$
$$K_{t+1}=K_t+sY_t-\delta K$$
$$A_{t+1}=(1+g)A_t,L_{t+1}=(1+n)L_t$$
$$K_1=A_1=L_1=1,s=0.1,\alpha=0.4,\delta=0.1,n=0.01,g=0.01$$
【追記:解答】
問1:効率労働一単位当たり資本遷移式(後述)を書け。
$$K_{t+1}=K_t+I_t-\delta K_t$$
$$=sF(K_t,A_tL_t)+(1-\delta )K_t$$
$$ここで効率労働AL1単位当たりで考えると$$
$$\frac{K_{t+1}}{A_t L_{t}}=\frac{sF(K_t,A_t L_t)}{A_t L_t}+(1-\delta )\frac{K_t}{A_t L_t}$$
$$\frac{K_{t+1}}{A_{t+1} L_{t+1}}\frac{A_{t+1}L_{t+1}}{A_t L_{t}}=sF \left( \frac{K_t}{A_t L_t},\frac{A_t L_t}{A_t L_t} \right)+(1-\delta )\frac{K_t}{A_t L_t}$$
$$k_{t+1}(1+g)(1+n)=sf(k_t)+(1-\delta )k_t$$
$$k_{t+1}=\frac{sf(k_t)+(1-\delta )k_t}{(1+g)(1+n)}$$
$$=\frac{sf(k_t) -(\delta +g + n+ gn)k_t}{(1+g)(1+n)}+k_t$$
問2:「効率労働一単位当たり資本の増加」「効率労働一単位当たり資本の減少」が一致する定常均衡において、「一人当たり」資本が毎期ごとに何倍になるのか答えなさい。
$$定常均衡k_{t+1}=k_tにおいて$$
$$\frac{sf(k_t) -(\delta +g + n+ gn)k_t}{(1+g)(1+n)}=0$$
$$sf(k_t) -(\delta +g + n+ gn)k_t=0$$
$$これで問1と似た図を作ることができ、大域的な安定性を持つ$$
$$なお、gnは無視できるほど小さいと考えれば$$
$$sf(k_t) -(\delta +g + n)k_t≒0と書き直せる$$
$$効率労働一単位当たり資本k_t=\frac{K_t}{A_t L_t}は一定$$
$$したがって一人当たり資本=\frac{K_t}{L_t}=\frac{K_t}{A_t L_t}A_tは技術進歩(1+g)で成長$$
問3:定常均衡において、「一人当たり」GDPが毎期ごとに何倍になるのか答えなさい。
$$生産関数が一次同次であることがポイントである$$
$$効率労働1単位当たりGDP=f(k_t)=F \left( \frac{K_t}{A_tL_t},\frac{A_tL_t}{A_tL_t} \right)の成長率はゼロで$$
$$一人当たりGDP=\frac{1}{L_t}F(K_t,A_tL_t)=F \left( \frac{K_t}{L_t},\frac{A_tL_t}{L_t} \right)=A_t F \left( \frac{K_t}{A_tL_t},\frac{A_tL_t}{A_tL_t} \right)$$
$$より一人当たりGDPは毎期(1+g)倍になる$$
問4:定常均衡において、「国のGDP」が毎期ごとに何倍になるのか答えなさい。
$$国のGDP=一人当たりGDP \times 人口より$$
$$毎期(1+g)(1+n)倍になる$$
問5:R言語を用いて「一人当たりGDP」についてのシミュレーションを実行せよ。
#変数説明
#Y=国全体GDP、国全体の資本=K、A=技術係数、L=労働L
#y=「一人」当たりGDP、c=一人当たり消費、k=一人当たり資本
#パラメーター
s <- 0.4 #貯蓄率
alpha <- 0.4 #資本分配率
d <- 0.1 #資本減耗率
n <- 0.01 #人口成長率
g <- 0.01 #技術進歩率
#初期値
A0 <- 1
L0 <- 1
K0 <- 1
#資本の遷移式
NextKapital <- function(K,Y,s,d) {
K_next <- K + s*Y - d*K
return(K_next)
}
#マクロ生産関数(国全体)
GDP <- function(K,A,L,alpha) {
Y <- (K^alpha)*((A*L)^(1-alpha))
return(Y)
}
#行列準備
T <- 100 #シミュレーション期間
Data<- data.frame(matrix(0,T,8))
colnames(Data) <- c("time","Y","K","A","L","y","c","k")
#初期値
Data[1,"time"] <- 1
Data[1,"A"] <- A0
Data[1,"L"] <- K0
Data[1,"K"] <- K0
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1) ){
K <- Data[t,"K"]
A <- Data[t,"A"]
L <- Data[t,"L"]
Y <- GDP(K,A,L,alpha)
C <- (1-s)*Y
Data[t,"Y"] <- Y
Data[t,"y"] <- Y/L
Data[t,"k"] <- K/L
Data[t,"c"] <- C/L
Data[t+1,"time"] <- 1 + Data[t,"time"]
Data[t+1,"A"] <- (1+g)*A
Data[t+1,"L"] <- (1+n)*L
Data[t+1,"K"] <- NextKapital(K,Y,s,d)
}
#最終期のデータ補完
Data[T,"Y"] <- GDP(Data[T,"K"],Data[T,"A"],Data[T,"L"],alpha)
Data[T,"y"] <- Data[T,"Y"]/Data[T,"L"]
Data[T,"c"] <- ((1-s)*Data[T,"Y"])/Data[T,"L"]
Data[T,"k"] <- Data[T,"K"]/Data[T,"L"]
#描画
plot(Data$time,Data$表示したい変数名)
plot(Data$time,Data$Y) #国全体のGDP(Y)の描画
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
ggplot(Data, aes(x = time))+
geom_line(aes(y = y,colour = "一人当たりGDP"))+
geom_point(aes(y = y,colour = "一人当たりGDP"))+
geom_line(aes(y = k/A,colour = "効率労働1単位当たり資本"))+
geom_point(aes(y = k/A,colour = "効率労働1単位当たり資本"))+
labs(color = "凡例")+
xlab("時間") +
ylab ("一人当たり変数") +
theme_grey(base_family = "HiraKakuPro-W3")