ソロー・モデルで行える規範的な分析は、一人当たり消費を最大にする定常均衡を導くことである。一人当たり国内総生産を最大にする定常均衡ではない。なぜなら、国内総生産Yはあくまでお金であり、消費Cしなければ効用Uにならない。そして、限界効用が正ならば、一人当たり消費最大点が一人一人の効用最大点となる。これで社会的望ましさ(社会厚生)に関する議論が可能にになる。異質な家計は想定しておらず、一人一人の消費行動は同じなので、以下のどの社会厚生関数でも「一人当たり消費最大点が社会的に最も望ましい」という結論は変わらない。
$$効用関数:U(c)=U \left( \frac{C}{L} \right)$$
$$ベンサム型社会厚生関数=\sum_{i=1}^{L} U_i(c_i)$$
$$ロールズ型社会厚生関数=\min \{ U_1(c_1),U_2(c_2),\cdots,U_L(c_L) \}$$
$$ニーチェ型社会厚生関数=\max \{ U_1(c_1),U_2(c_2),\cdots,U_L(c_L) \}$$
$$なお、Lは人口を意味する。Lが自然数のときを\sumで表現した$$
一人当たり消費が最大になる定常均衡を実現する条件を、経済成長の黄金律(golden rule of economic growth)という。画像1のように貯蓄率sを変化させることで、定常均衡で実現する消費が変化する。結論は「資本の限界生産性≒資本減耗率+技術進歩率+人口成長率で消費が最大」である。詳しい解説は追記した。
$$f'(k)=\delta +g + n+ gn≒\delta +g + nが黄金律$$
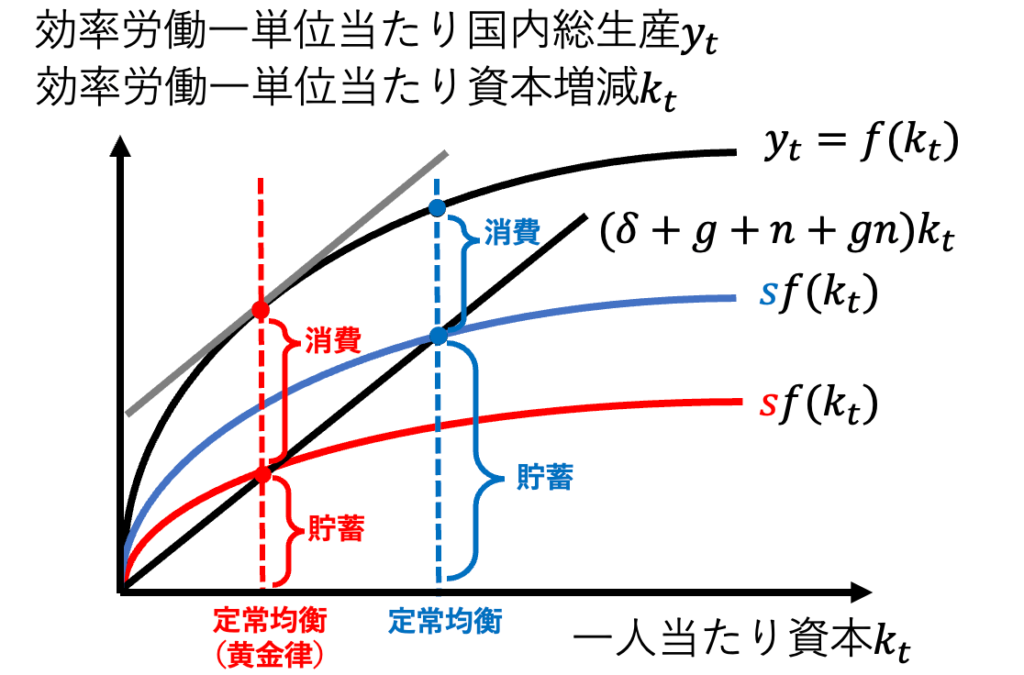
ソロー・モデルでは、貯蓄率sが外生的に決まるため、経済成長の黄金律が実現するとは限らない。つまり、パレート改善が可能であり、パレート最適でない経済状態が実現しうる。もっと言えば、ベンサム型、ロールズ型、ニーチェ型のすべての社会厚生関数が最大化されていない経済状態が実現しうる。実は、ソロー・モデルに市場メカニズムを導入することで、パレート最適な経済が実現される。詳しい話は、最適成長モデル(ラムゼイ・モデル)を学んで欲しいが、その前に読者はミクロ経済学を学ばなければならない。
【追記:問題】
問1:一人当たり消費をf(k)を含む形で導け。ここでのkは効率労働一単位当たりの資本K/ALである。
問2:一人当たり消費が最大になる効率労働一単位当たり資本が満たすべき条件を導け。ただし、次の事実を用いてよい。
$$定常均衡ではsf(k) -(\delta +g + n+ gn)k=0$$
問3:人口成長がゼロならば、経済成長の黄金律にて、利子率r=技術進歩率gとなることを示せ。「資本所得と労働所得の成長について」問2の次の結果を用いてよい。
$$定常均衡にてr_t=f'(k) – \delta$$
【追記:解答】
問1:一人当たり消費をf(k)を含む形で導け。ここでのkは効率労働一単位当たりの資本K/ALである。
$$c=(1-s) y$$
$$=(1-s) \frac{F(K,AL)}{L}$$
$$=(1-s) \frac{F(K,AL)}{L}\frac{A}{A}$$
$$=(1-s) A \frac{F(K,AL)}{AL}$$
$$=(1-s) A F \left( \frac{K}{AL},\frac{AL}{AL} \right)$$
$$=A f(k)-sA f(k) ただしk=\frac{K}{AL}$$
問2:一人当たり消費が最大になる効率労働一単位当たり資本が満たすべき条件を導け。ただし、次の事実を用いてよい。
$$定常均衡ではsf(k) -(\delta +g + n+ gn)k=0$$
$$sf(k) =(\delta +g + n+ gn)k$$
$$よってc=A f(k)-(\delta +g + n+ gn)Ak$$
$$消費が最大になるのは$$
$$\frac{d c}{d k}=A f'(k)-(\delta +g + n+ gn)A=0$$
$$したがってf'(k)=\delta +g + n+ gnが黄金律である。$$
$$そして、gnは無視できるほど小さいと考えると$$
$$資本の限界生産性≒\delta +g + nが黄金律である。$$
問3:人口成長がゼロならば、経済成長の黄金律にて、利子率r=技術進歩率gとなることを示せ。「資本所得と労働所得の成長について」問2の次の結果を用いてよい。
$$定常均衡にてr=f'(k) – \delta$$
$$黄金律にてf'(k)=\delta +g + n+ gn$$
$$人口成長がゼロならf'(k)=\delta +g$$
$$定常均衡であるのでf'(k)= r+ \delta$$
$$よって\delta +g=f'(k)= r+ \deltaよりr=g$$
$$経済成長の黄金律にて利子率は技術進歩率に等しい$$
