ソロー・モデルにおける定常均衡では、一人当たりの労働所得と資本所得は技術進歩率で成長する。それは次の3点の結論によって実現される。第1に、賃金が技術進歩率で増大する。第2に、利子率は一定になる。第3に、一人当たり資本が技術進歩率で増大する。
$$一人当たり労働所得=\frac{w_t L_t }{ L_t}=w_t$$
$$一人当たり資本所得=\frac{r_t K_t}{ L_t}$$
適当なパラメーターを用いて、ソロー・モデルのシミュレーションしてみた結果が画像1である。100期以降では、一人当たり労働所得(赤)、一人当たり資本所得(緑)の成長率は同じである。そして、利子率は一定である。なお、今回シミュレーションしたパラメーターの下では、利子率は約2%で一定になった。
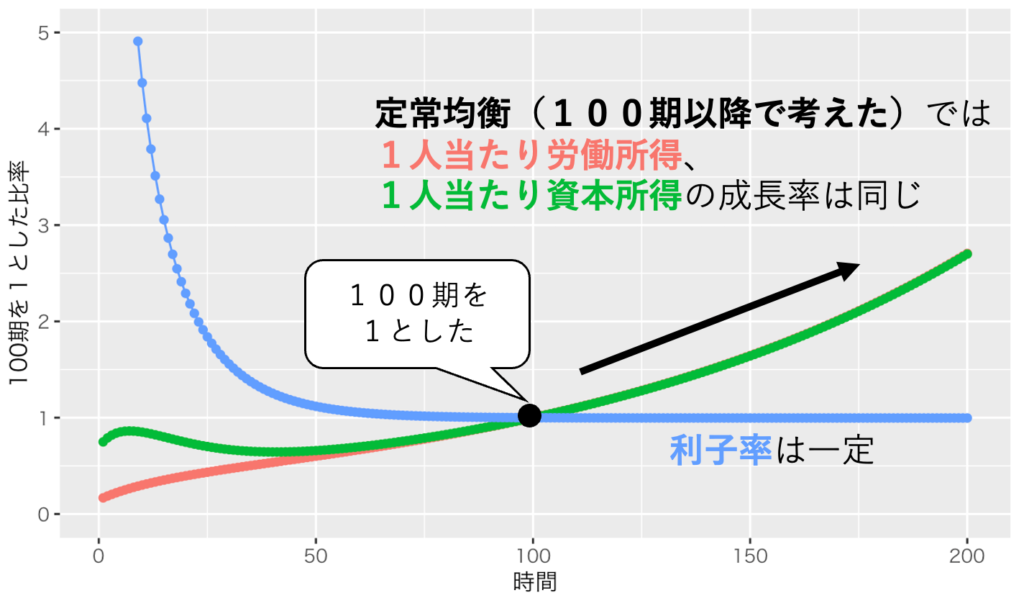
定常均衡に到達すれば、労働所得と資本所得の格差は拡大せず、双方が技術進歩の恩恵を受けられる。なお、注意しておくべきは、ソローモデルにて人々は労働者であり、資本家であるということだ。したがって、労働者階級、資本家階級のような異質な家計での格差が拡大するか否かまで踏み込んでは分析していないことは付記しておく。
【追記:モデルの詳細】
モデルの直感的な解説は「ソロー成長モデルについて」をみてほしい。
アルファベットの意味は「t:離散的な時間。自然数。time」「Y:国内総生産。Yield」「F:マクロ生産関数。Function」「K:資本。Kapital(ドイツ語)」「A:技術係数。Art」「L:労働(=人口)。Labor」「I:投資。Investment」「S:貯蓄。Saving」「g:技術進歩率。Growth」「n:人口成長率。Number」「δ:固定資本減耗率。fixed capital Depreciation rate)。また、モデルを解く際は「効率労働:AL」とし、効率労働一単位当たりの資本、生産関数などを小文字で表すことが多い。例えば、k=K/AL、f(k)=F(K/AL,1)。
$$【家計】$$
$$投資:S_t=sY_t$$
$$貯蓄率s一定を仮定:s_t=s$$
$$これはクズネッツ型消費関数$$
$$【企業】$$
$$国内総生産:Y_t=F(K_t,A_tL_t)$$
$$ただし、マクロ生産関数は次の3条件を満たす。$$
$$限界生産性は正:\frac{\partial Y}{\partial K}>0,\frac{\partial Y}{\partial L}>0$$
$$↑生産要素を増やせば生産量は必ず増える$$
$$限界生産性逓減:\frac{\partial^2 Y}{\partial K^2} <0,\frac{\partial^2 Y}{\partial L^2} <0$$
$$↑生産要素を増やせば、増える生産量は必ず減っていく$$
$$規模に対して収穫一定:F(\lambda K, \lambda AL)=\lambda F(K, AL)$$
$$↑資本Kと効率労働ALを2倍にしたら生産性変わらず生産量Yは2倍$$
$$↑数学的には1次同次という。$$
$$↑n次同次:F(\lambda K, \lambda AL)=\lambda^n F(K, AL)$$
$$【財市場均衡条件】$$
$$Y_t=C_t+I_t$$
$$生産面のGDP:Y_t$$
$$支出面のGDP:C_t+I_t$$
$$財供給F(K_t,A_t L_t)側が需要(C_t+I_t)を決定$$
$$なお、政府部門G_t、海外部門NX_tを無視$$
$$【金融市場均衡条件】$$
$$投資:S_t=I_t$$
$$資金供給S_t側が資金需要I_tを決定$$
$$I_t(r_t)と考え利潤最大化問題を解けば利子率r_tを得られる$$
$$【労働市場均衡条件】$$
$$労働:L_t^{供給}=L_t^{需要}$$
$$労働供給L_t^{供給}側が労働需要L_t^{需要}を決定$$
$$L_t^{需要}(w_t)と考え利潤最大化問題を解けば賃金w_tを得られる$$
$$【動学モデル】$$
$$資本遷移式:K_{t+1}=K_t+I_t-\delta K_t$$
$$=sF(K_t,A_tL_t)+(1-\delta)K_t$$
$$マルサス型の指数関数的人口成長L_{t+1}=(1+n)L_t$$
$$外生的な技術進歩:A_{t+1}=(1+g)A_t$$
$$【企業についての補足】$$
$$生産関数を特定化して考えたい場合は$$
$$F(K_t,A_tL_t)=K_t^\alpha (A_tL_t)^{1-\alpha}$$
$$0<\alpha<1。\alphaは資本分配率と解釈できる。$$
$$のコブ・ダグラス型を使って良い。これは上の3条件を満たす。$$
$$ただし、ソロー・モデルの結論は3条件が満たされる生産関数なら成り立つ。$$
【追記:問題】
問1:企業の利潤最大化問題を解いて、利子率と賃金についての式を導け。(一階条件)
$$\max 利潤=収入 – 人件費 – 資本レンタル料 – 資本減耗$$
$$\max F(K_t,A_t L_t) – w_t L_t – (r_t + \delta)K_t$$
問2:定常均衡における利子率を求めよ。効率労働AL1単位当たりの変数は小文字で表すと、定常均衡とは次のことが成り立つ。なお、一次同次の生産関数を仮定しているので、ヒントを用いてよい。
$$効率労働1単位当たり資本 \frac{K_t}{A_t L_t}=k_t$$
$$定常均衡:k_{t+1}=k_t(=k)$$
$$ヒント:f(k_t)=F \left( \frac{K_t}{A_t L_t},1 \right)=\frac{1}{A_t L_t}F( K_t, A_t L_t)$$
問3:定常均衡における一人当たり資本所得が技術進歩率で決まることを示せ。
$$定義:一人当たり資本所得=\frac{r_t K_t}{ L_t}$$
$$ヒント:定常均衡がk_{t+1}=k_t(=k)ならば$$
$$\frac{K_{t+1}}{A_{t+1} L_{t+1}}=\frac{K_{t}}{A_{t} L_{t}}$$
問4:定常均衡にて賃金が毎期ごとに(1+g)倍になることを示せ。
問5:定常均衡にて一人当たり労働所得が毎期ごとに(1+g)倍になることを示せ。
$$定義:一人当たり労働所得=\frac{w_t L_t }{ L_t}$$
問6:一人当たり労働所得と一人当たり資本所得の伸び率が一致することを示せ。さらに、それは伸び率が技術進歩によって決定されることを示せ。
問7:本文の画像1をシミュレーションによって出力せよ。ただし、以下のモデルを用いよ。また、定常均衡は100期に達したとみなして、100期の各変数で1~200期の変数を割ってやるとよい。
$$Y_t=F(K_t,A_t L_t)=K_t^\alpha (A_t L_t)^{1-\alpha}$$
$$K_{t+1}=K_t+sY_t-\delta K$$
$$A_{t+1}=(1+g)A_t,L_{t+1}=(1+n)L_t$$
$$K_1=A_1=L_1=1,s=0.1,\alpha=0.4,\delta=0.1,n=0.01,g=0.01$$
問8:定常均衡にて、一人当たり労働所得と一人当たり資本所得の伸び率が一致していることは、問7までで確認した。では、量はどうなのだろうか。100期の各変数で1~200期の変数を割ってやらないでシミュレーションせよ。さらに、次の両方についてシミュレーションせよ。
$$一人当たり実質資本所得=\frac{r_t K_t}{ L_t}$$
$$一人当たり名目資本所得=\frac{(r_t+\delta) K_t}{ L_t}$$
【追記:解答】
問1:企業の利潤最大化問題を解いて、利子率と賃金についての式を導け。(一階条件)
$$\max 利潤=収入 – 人件費 – 資本レンタル料 – 資本減耗$$
$$\max F(K_t,A_t L_t) – w_t L_t – (r_t + \delta)K_t$$
$$一階条件より$$
$$\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – (r_t + \delta)=0$$
$$\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} -w_t=0$$
$$したがって$$
$$r_t=\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – \delta$$
$$w_t=\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} である。$$
問2:定常均衡における利子率を求めよ。効率労働AL1単位当たりの変数は小文字で表すと、定常均衡とは次のことが成り立つ。なお、一次同次の生産関数を仮定しているので、ヒントを用いてよい。
$$効率労働1単位当たり資本 \frac{K_t}{A_t L_t}=k_t$$
$$定常均衡:k_{t+1}=k_t(=k)$$
$$ヒント:f(k_t)=F \left( \frac{K_t}{A_t L_t},1 \right)=\frac{1}{A_t L_t}F( K_t, A_t L_t)$$
$$企業の利潤最大化の一階条件より$$
$$r_t=\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – \deltaである。$$
$$よって、定常均衡にて\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} が一定であることを示せばよい$$
$$定常均衡では$$
$$\frac{\partial F(K,A L) }{ \partial K}=\frac{\partial F(K,A L) }{ \partial \frac{K}{A L}}\frac{\partial \frac{K}{A L} }{ \partial K}$$
$$=\frac{\partial A L F(\frac{K}{A L},1) }{ \partial \frac{K}{A L}}\frac{\partial \frac{K}{A L} }{ \partial K} 一次同次より$$
$$=AL \frac{\partial f(k) }{ \partial k}\frac{1}{A L}$$
$$=\frac{\partial f(k) }{ \partial k}$$
$$kは一定なので、\frac{\partial F(K,A L) }{ \partial K} は一定。$$
$$したがって定常均衡にてr_t=\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – \deltaも一定$$
問3:定常均衡における一人当たり資本所得が技術進歩率で決まることを示せ。
$$ヒント:定常均衡がk_{t+1}=k_t(=k)ならば$$
$$\frac{K_{t+1}}{A_{t+1} L_{t+1}}=\frac{K_{t}}{A_{t} L_{t}}$$
$$\frac{K_{t+1}}{L_{t+1}}=A_{t+1}\frac{K_{t}}{A_{t} L_{t}}=(1+g)\frac{K_{t}}{ L_{t}}$$
$$一人当たり資本所得=\frac{r_t K_t}{ L_t}だが、$$
$$利子率r_tは定常均衡で一定。\frac{K_t}{L_t}は技術進歩で成長するので$$
$$一人当たり資本所得は毎期ごとに(1+g)倍になる$$
問4:定常均衡にて賃金が毎期ごとに(1+g)倍になることを示せ。
$$企業の利潤最大化の一階条件より$$
$$w_t=\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} である。$$
$$よって、\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} が技術進歩で成長することを示せばよい。$$
$$定常均衡では$$
$$\frac{\partial F(K,A L) }{ \partial L}=\frac{\partial F(K,A L) }{ \partial \frac{K}{A L}}\frac{\partial \frac{K}{A L} }{ \partial L}$$
$$\frac{\partial A L F(\frac{K}{A L},1) }{ \partial \frac{K}{A L}}\frac{\partial \frac{K}{A L} }{ \partial L}$$
$$=AL \frac{\partial f(k) }{ \partial k}\frac{K}{A L^2}$$
$$=\frac{\partial f(k) }{ \partial k}\frac{K}{L}$$
$$kは一定なので、\frac{\partial f(k) }{ \partial k} は一定。$$
$$ただし、\frac{K}{L}は技術進歩で増大する。$$
$$よって、\frac{\partial F(K_t,A_t L_t) }{ \partial L_t}は毎期ごとに(1+g)倍になる。$$
$$したがって、w_tは毎期ごとに(1+g)倍になる。$$
問5:定常均衡にて労働所得が毎期ごとに(1+g)倍になることを示せ。
$$一人当たり労働所得=\frac{w_t L_t }{ L_t}=w_t$$
$$そして、w_tは毎期ごとに(1+g)倍になるので、示された。$$
問6:労働所得と資本所得の伸び率が一致することを示せ。さらに、それは伸び率が技術進歩によって決定されることを示せ。
$$労働所得と資本所得は毎期ごとに(1+g)倍になる。$$
$$gは技術進歩率。よって示された。$$
問7:本文の画像1をシミュレーションによって出力せよ。ただし、以下のモデルを用いよ。また、定常均衡は100期に達したとみなして、100期の各変数で1~200期の変数を割ってやるとよい。
$$Y_t=F(K_t,A_t L_t)=K_t^\alpha (A_t L_t)^{1-\alpha}$$
$$K_{t+1}=K_t+sY_t-\delta K$$
$$A_{t+1}=(1+g)A_t,L_{t+1}=(1+n)L_t$$
$$K_1=A_1=L_1=1,s=0.1,\alpha=0.4,\delta=0.1,n=0.01,g=0.01$$
#変数説明
#Y=国全体GDP、国全体の資本=K、A=技術係数、L=労働L
#y=「一人」当たりGDP、c=一人当たり消費、k=一人当たり資本
#パラメーター
s <- 0.4 #貯蓄率
alpha <- 0.4 #資本分配率
d <- 0.1 #資本減耗率
n <- 0.01 #人口成長率
g <- 0.01 #技術進歩率
#初期値
A0 <- 1
L0 <- 1
K0 <- 1
#資本の遷移式
NextKapital <- function(K,Y,s,d) {
K_next <- K + s*Y - d*K
return(K_next)
}
#マクロ生産関数(国全体)
GDP <- function(K,A,L,alpha) {
Y <- (K^alpha)*((A*L)^(1-alpha))
return(Y)
}
#利子率
rental_price <- function(K,A,L,alpha,d) {
r <- alpha*(K^(alpha-1))*((A*L)^(1-alpha)) -d
return(r)
}
#賃金
wage <- function(K,A,L,alpha) {
w <- (1-alpha)*(K^(alpha))*(A^(1-alpha))*L^(-alpha)
return(w)
}
#行列準備
T <- 201 #シミュレーション期間+1
Data<- data.frame(matrix(0,T,12))
colnames(Data) <- c("time","Y","K","A","L","y","c","k","w","r","labor_income","capital_income")
#初期値
Data[1,"time"] <- 1
Data[1,"A"] <- A0
Data[1,"L"] <- K0
Data[1,"K"] <- K0
#シミュレーション(1期から(T-1)期まで)
for(t in 1:(T-1) ){
K <- Data[t,"K"]
A <- Data[t,"A"]
L <- Data[t,"L"]
Y <- GDP(K,A,L,alpha)
C <- (1-s)*Y
Data[t,"Y"] <- Y
Data[t,"y"] <- Y/L
Data[t,"k"] <- K/L
Data[t,"c"] <- C/L
Data[t,"r"] <- rental_price(K,A,L,alpha,d)
Data[t,"w"] <- wage(K,A,L,alpha)
Data[t,"labor_income"] <- (wage(K,A,L,alpha))
Data[t,"capital_income"] <- (rental_price(K,A,L,alpha,d)*K)/L
Data[t+1,"time"] <- 1 + Data[t,"time"]
Data[t+1,"A"] <- (1+g)*A
Data[t+1,"L"] <- (1+n)*L
Data[t+1,"K"] <- NextKapital(K,Y,s,d)
}
#描画
plot(Data$time,Data$表示したい変数名)
plot(Data$time,Data$Y) #国全体のGDP(Y)の描画
#描画(ggplot2)
#install.packages("ggplot2") ggplot2未インストールの方は実行
library(ggplot2)
#問7:比率
ggplot(Data, aes(x = time))+
geom_line(aes(y = labor_income/Data[TT,"labor_income"],colour = "一人当たり労働所得"))+
geom_point(aes(y = labor_income/Data[TT,"labor_income"], colour = "一人当たり労働所得"))+
geom_line(aes(y = capital_income/Data[TT,"capital_income"],colour = "一人当たり資本所得"))+
geom_point(aes(y = capital_income/Data[TT,"capital_income"],colour = "一人当たり資本所得"))+
geom_line(aes(y = r/Data[TT,"r"],colour = "利子率"))+
geom_point(aes(y = r/Data[TT,"r"],colour = "利子率"))+
labs(color = "凡例")+
xlab("時間") +
ylab ("100期を1とした比率") +
scale_x_continuous(limits=c(1,200))+
scale_y_continuous(limits=c(0,5))+
theme_grey(base_family = "HiraKakuPro-W3")
#問8:量
ggplot(Data, aes(x = time))+
geom_line(aes(y = labor_income,colour = "一人当たり労働所得"))+
geom_point(aes(y = labor_income, colour = "一人当たり労働所得"))+
geom_line(aes(y = capital_income,colour = "一人当たり実質資本所得"))+
geom_point(aes(y = capital_income,colour = "一人当たり実質資本所得"))+
geom_line(aes(y = (r+d)*(K/L),colour = "一人当たり名目資本所得"))+
geom_point(aes(y = (r+d)*(K/L),colour = "一人当たり名目資本所得"))+
labs(color = "凡例")+
xlab("時間") +
ylab ("100期を1とした比率") +
scale_x_continuous(limits=c(1,200))+
scale_y_continuous(limits=c(0,10))+
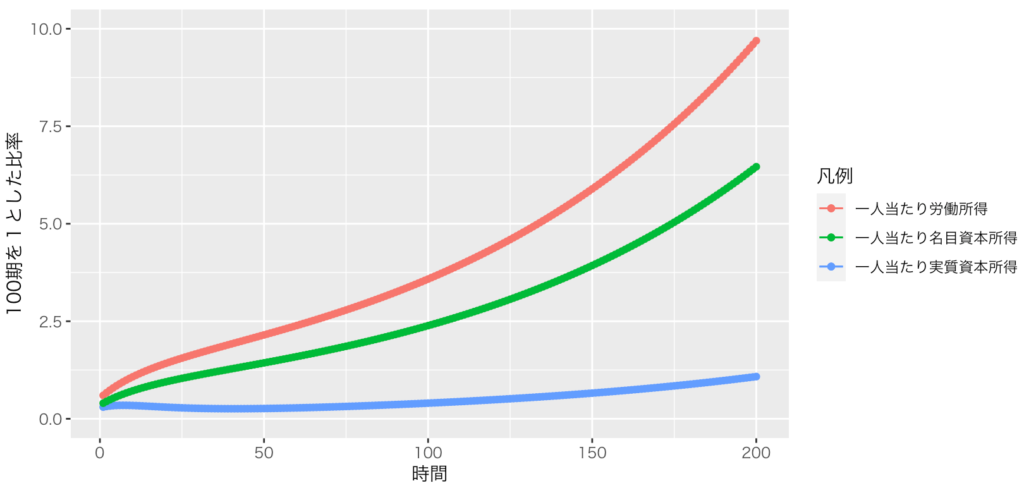
theme_grey(base_family = "HiraKakuPro-W3")問8:定常均衡にて、一人当たり労働所得と一人当たり資本所得の伸び率が一致していることは、問7までで確認した。では、量はどうなのだろうか。100期の各変数で1~200期の変数を割ってやらないでシミュレーションせよ。さらに、次の両方についてシミュレーションせよ。
$$一人当たり実質資本所得=\frac{r_t K_t}{ L_t}$$
$$一人当たり名目資本所得=\frac{(r_t+\delta) K_t}{ L_t}$$
#問7のコード最後をみよ。