この記事では難しいニューケインジアン・モデルのわかりやすいモデルに近似する。具体的には、インフレゼロの定常均衡まわりでの対数線形近似モデルを作る。なぜならば、ミクロ的基礎づけから導かれたニューケインジアン・モデルのマクロ経済変数に関する方程式は、非線形で、ぐにゃぐにゃしており、わかりにくいからである。
難しい問題について議論するときの定番は定常均衡について議論することであるが、その発展系が「少しだけ定常均衡からずれている+今後定常均衡に戻る」という状態について議論することである。これが対数線形近似の発想である。基準となる定常均衡が必要だが「インフレゼロの定常均衡」との乖離具合によって議論しよう。
しかし絡まった糸を解くには、あまりやりたくない下処理をしなければならない。なので、この記事もスキップしてよい。結論だけ下に残しておく。
・小文字の変数はインフレゼロの定常均衡との乖離率を意味する。ただし、利子率i,rとインフレ率πはそのままの意味。
$$GDPギャップ:y_t=\frac{Y_t-Y^*_{インフレゼロの定常均衡^*}}{Y^*_{インフレゼロの定常均衡^*}}$$
$$ネット名目利子率i_t、ネット自然利子率r^*、ネットインフレ率\pi_t$$
・オイラー方程式+フィッシャー方程式
$$y_t=y_{t+1}-\frac{1}{\chi_C}(i_t-r^*-\pi_t)$$
・ニューケインジアン・フィリップス曲線
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1) (\chi_L+\chi_C)}{\phi_m} y_t$$
・足りていない方程式=名目利子率i決定に関する金融政策ルール
・中央銀行の社会厚生関数
$$中央銀行の社会厚生関数W_{中央銀行}(y_t,\pi_t)$$
$$=- \frac{1}{2} \left( \pi_t ^2 +\lambda ( y_t-y_g)^2 \right) $$
$$ただし、y_g=\frac{\lambda_g}{\lambda}=\frac{\theta-(\theta-1)(1+g)}{\theta \chi_C+\chi_L (\theta-1)(1+g)}$$
$$\lambda_g=\frac{\theta-(\theta-1)(1+g)}{(\theta-1)(1+g) \phi_m}$$
$$\lambda=\frac{\theta \chi_C+\chi_L (\theta-1)(1+g) }{(\theta-1)(1+g) \phi_m}$$
$$国民の社会厚生関数W_{国民}(y_t,\pi_t)$$
$$=- \frac{1}{2} \left( \pi_t ^2 +\lambda y_t^2 \right)$$
「ニューケインジアン・モデル」解説シリーズ
企画:「しまうま総研 より良い社会のための思考法 / 3段落で簡潔明瞭」>「よりよい社会のための経済学入門」>「ニューケインジアン・モデルについて」
第1回:ニューケインジアン・モデルについて(必読 / 難易度中)
第2回:家計、最終財企業、中間財企業、市場均衡条件のミクロ的基礎について (スキップ可 / 難易度高)
第3回:非線形動学と非線形定常均衡について(スキップ可 / 難易度高)
第4回:対数線形化と対数線形近似について(スキップ可 / 難易度高)
第5回:GDPギャップとインフレの社会厚生について
第5回:テイラー・ルールと定常均衡について
第6回:中間財市場と最適財政政策について(必読 / 難易度中)
第7回:労働市場と非効率な雇用水準について
第8回:最終財市場とGDPギャップについて
第9回:独占的競争と短期なインフレについて
第10回:粘着的な価格とインフレの平準化について
第11回:最適金融政策とインフレ・バイアスについて
第12回:動学的確率的一般均衡モデルへの拡張について
第13回:Dynareを用いたシミュレーションについて
補講:DynareをMATLABで動かすための環境構築について / DynareをOctaveで動かすための環境構築について
主要な参考資料
・仲田泰祐(2020)「ゼロ金利制約下の 金融政策 FRBの政策運営」 (モデルは仲田(2020)と同じ)
・楡井誠(2023)「マクロ経済動学: 景気循環の起源の解明」
前提
・【仮定】対数線形近似は、「実現する経済」が「インフレ率0の定常均衡」と十分に近いことを仮定している。この仮定は、対数線形近似せずに非線形モデルのまま解くのならば、回避することができる。非線形モデルのまま解く代表的な手法が、動的計画法(DP, Dynamic Programming)である。
・【定義】グロスGrossとネットNetの違い。グロスは総、ネットは純と訳される。日常生活で使うインフレ率や利子率はネットの数値をパーセントにしたもの。つまり、ネットの数値に100を掛けたもの。
$$グロスインフレ率\Pi_t=1+ネットインフレ率\pi_t$$
$$グロス名目利子率I_t=1+ネット名目利子率i_t$$
・【定義】*つき変数大文字X*=ネットインフレ率0での定常均衡におけるX。
・【定義】小文字x=ネットインフレ率0での定常均衡からの乖離率。ただし、インフレ率、利子率、補助金率の小文字は、そのまま、ネットインフレ率、ネット利子率、ネット補助金率を意味する。
$$x_t =\frac{X_t-X^*}{X^*}$$
$$\pi_t=ネットインフレ率\pi_t$$
$$i_t=ネット名目利子率i_t$$
$$g=ネット補助金率g$$
・【定義】^つき変数^大文字Xの定義=「実現した経済X」と「ネットインフレ率0での定常均衡におけるX*」の対数差。
$$\widehat{X_t}=\log(X_t)-\log(X^*)$$
・【近似】ネットインフレ率0での定常均衡からの乖離率に近似できる。
$$\widehat{X_t}=\log(X_t)-\log(X^*)≒x_t=\frac{X_t-X_{インフレゼロの定常均衡^*}}{X_{インフレゼロの定常均衡^*}}$$
なお、グロスインフレ率Π、グロス利子率Iは、ネットインフレ率0での定常均衡からの乖離差に近似できる。
$$\widehat{\Pi_t}=\log(\Pi_t)-\log(\Pi^*)=\log(1+\pi_t)-\log(1)≒\pi_t$$
$$\widehat{I_t}=\log(I_t)-\log(I^*)=\log(1+i_t)-\log(1+r^*)≒i_t-r^*$$
問A:対数線形化と対数線形近似
問A-1 対数線形化
問A-1(対数線形化) 次のログの近似式と全微分から、線形対数化の式を導け。
$$線形対数化:dF(X,Y)=\frac{\partial F(X^*,Y^*)}{\partial X} X^* d \log(X^*)+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^*d \log(Y^*)$$
$$ただし、d \log(X^*)=\log(X^*+dX)-\log(X^*)$$
$$全微分:(dX,dY)→(0,0)ならば、(X,Y)=(X^*,Y^*)にて$$
$$dF(X^*,Y^*)=\frac{\partial F(X^*,Y^*)}{\partial X} dX+\frac{\partial F(X^*,Y^*)}{\partial Y} dY$$
(解答)
$$dF(X,Y)=\frac{\partial F(X^*,Y^*)}{\partial X} dX+\frac{\partial F(X^*,Y^*)}{\partial Y} dY$$
$$=\frac{\partial F(X^*,Y^*)}{\partial X} X^* \frac{dX}{X^*}+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^* \frac{dY}{Y^*}$$
$$=\frac{\partial F(X^*,Y^*)}{\partial X} X^*( \log(X^*+dX)-\log(X^*))$$
$$+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^* *( \log(Y^*+dY)-\log(Y^*))$$
$$=\frac{\partial F(X^*,Y^*)}{\partial X} X^* d \log(X)+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^*d \log(Y)$$
問A-2:対数線形近似
問A-2:(X*,Y*)がインフレ率0、自然利子率r*の定常均衡だとして、対数線形化の式を対数線形近似として解釈せよ。
$$ログの近似:\log(X^*+dX)-\log(X^*)≒\frac{dX}{X^*}$$
$$インフレ率0、自然利子率r*の定常均衡からの乖離率=\frac{X_t-X^*}{X^*}=\frac{dX}{X^*}$$
$$なお、後ほど\widehat{X_t}=\frac{X_t-X^*}{X^*}と定義する。$$
(2)
$$dF(X,Y)=\frac{\partial F(X^*,Y^*)}{\partial X} X^* d \log(X)+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^*d \log(Y)$$
$$≒\frac{\partial F(X^*,Y^*)}{\partial X} X^* (Xの乖離率)+\frac{\partial F(X^*,Y^*)}{\partial Y} Y^* (Yの乖離率)$$
問B:非線形ニューケインジアン・モデルの対数線形化
問B-1(対数線形化) オイラー方程式
問B-1(対数線形化)次のオイラー方程式をインフレ率0の定常均衡周りで対数線形化せよ。グロス名目利子率をI=1+i、グロスインフレ率をΠ=1+πで表して計算せよ。また、対数差は上に^をつけて表現せよ。なお、このニューケインジアンモデルでは、資本Kは無視されており、投資Iの文字を使っていないので、アルファベットの重複は気にしなくてよい。また、必要であれば、次を用いよ。
$$\log(\Pi_{t})=\log(1+\pi_{t})≒\pi_{t}、\log(I_{t})=\log(1+i_{t})≒i_{t}$$
$$C_{t+1}^{\chi_C} \frac{\beta (1+i_t)}{1+\pi_{t+1}} = C_{t}^{\chi_C}$$
$$→C_{t+1}^{\chi_C} \frac{\beta I_t}{\Pi_{t+1}} = C_{t}^{\chi_C}$$
$$ただし、I_t=1+i_t、\Pi_t=1+\pi_tである。$$
$$表記例:\widehat{C_t}=d \log(C_t)= \log(C_t) – \log(C^*) ≒\frac{C_t- C^*}{C^*}$$
次のように関数FとGをセットする。
$$F(C_{t+1}, I_t,\Pi_{t+1})=C_{t+1}^{\chi_C} \frac{\beta I_t}{\Pi_{t+1}}$$
$$G(C_{t}) = C_{t}^{\chi_C}$$
F=GよりdF=dGである。
$$メモ:F(C_{t+1}, I_t,\Pi_{t+1})=C_{t+1}^{\chi_C} \frac{\beta I_t}{\Pi_{t+1}}$$
$$d F=\frac{\partial F(C^*, I^*,\Pi^*)}{\partial C_{t+1}} C^* d \log(C_{t+1})$$
$$+\frac{\partial F(C^*, I^*,\Pi^*)}{\partial I_t} I^* d \log(I_t)$$
$$+\frac{\partial F(C^*, I^*,\Pi^*)}{\partial \Pi_t} C^* d \log(\Pi_{t+1})$$
$$=\left( \chi_C (C^*)^{\chi_C-1} \frac{\beta I^*}{\Pi^*} \right) C^* d \log(C_{t+1})$$
$$+\left( (C^*)^{\chi_C} \frac{\beta }{\Pi^*} \right) I^* d \log(I_{t})$$
$$+\left( (-1) (C^*)^{\chi_C} \frac{\beta I^*}{(\Pi^*)^2} \right) \Pi^* d \log(\Pi_{t+1})$$
$$=\chi_C (C^*)^{\chi_C} \frac{\beta I^*}{\Pi^*} d \log(C_{t+1})$$
$$+ (C^*)^{\chi_C} \frac{\beta I^*}{\Pi^*} d \log(I_{t})$$
$$ -(C^*)^{\chi_C} \frac{\beta I^*}{\Pi^*} d \log(\Pi_{t+1})$$
ここが工夫なのだが
$$F^*=F(C^*, I^*,\Pi^*)=(C^*)^{\chi_C} \frac{\beta I^*}{\Pi_{t^*}}とすると$$
$$d F≒\Big( \chi_C d \log(C_{t+1}) +d \log(I_{t})-d \log(\Pi_{t}) \Big)F^*$$
次にGである。
$$メモ:G(C_{t}) = C_{t}^{\chi_C}$$
$$d G=\frac{\partial G(C^*)}{\partial C_{t}} C^* d \log(C_{t})$$
$$=\chi_C (C^*)^{\chi_C-1} C^* d \log(C_{t})$$
$$=\chi_C d \log(C_{t}) G^* なおG^*=G(C^*) = (C^*)^{\chi_C}$$
d F=d G、F*=G*より
$$(\chi_C d \log(C_{t+1}) +d \log(I_{t})-d \log(\Pi_{t}))F^*=\chi_C d \log(C_{t}) G^*$$
$$\chi_C d \log(C_{t+1}) +d \log(I_{t})-d \log(\Pi_{t})=\chi_C d \log(C_{t}) $$
$$\log(C_{t})=d \log(C_{t+1}) – \frac{1}{\chi_C} \Big( d \log(I_{t})-d \log(\Pi_{t+1}) \Big)$$
$$ここで表記を\widehat{C_t}=d \log(C_t) ≒\frac{C_t- C^*}{C^*}のように対数線形近似を用いると$$
$$\widehat{C_t}=\widehat{C_{t+1}}-\frac{1}{\chi_C} (\widehat{I_t} -\widehat{\Pi_{t+1}})$$
問B-2(対数線形化) 労働余暇選択式
問B-2(対数線形化)次の労働余暇選択式をインフレ率0の定常均衡周りで対数線形化せよ。また、対数差は上に^をつけて表現せよ。
$$w_t=L_t^{\chi_L} C_t^{\chi_C}$$
$$F(W_t)=w_t、G(L_t,C_t)=L_t^{\chi_L} C_t^{\chi_C}とおくと$$
Fについて
$$dF(W_t)=w^* d \log(w_t)= d \log(w_t) F^*$$
Gについて
$$G(L_t,C_t)=\frac{\partial G(L^*, C^*)}{\partial L_{t}} L^* d \log(L_{t})$$
$$+\frac{\partial G(L^*, C^*)}{\partial C_t} I^* d \log(C_t)$$
$$=\chi_L (L^*)^{\chi_L-1} (C^*)^{\chi_L} L^* d \log(L_{t})$$
$$+\chi_C \frac{\partial F(L^*, C^*)}{\partial C_t} I^* d \log(C_t)$$
$$=\Big( \chi_L d \log(L_{t})+\chi_C d \log(C_{t}) \Big) G^*$$
dF=dGとF*=G*より
$$d \log(w_t) F^*=\Big( \chi_L d \log(L_{t})+\chi_C d \log(C_{t}) \Big) G^*$$
$$d \log(w_t) = \chi_L d \log(L_{t})+\chi_C d \log(C_{t}) $$
$$ここで表記を\widehat{C_t}=d \log(C_t) ≒\frac{C_t- C^*}{C^*}のようにあらためると$$
$$\widehat{w_t}=\chi_L \widehat{L_t}+\chi_C \widehat{C_t}$$
問B-3(対数線形化) ニューケインジアン・フィリップス曲線
問B-3(対数線形化)次のニューケインジアン・フィリップス曲線をインフレ率0の定常均衡周りで対数線形化せよ。また、対数差は上に^をつけて表現せよ。グロスインフレ率をΠ=1+πで表して計算せよ。
$$\phi_m \pi_t (1+\pi_t) =(1+g)(1- \theta ) + \theta w_t + \beta \left( \frac{C_t}{C_{t+1}} \right) ^{\chi_c} \left( \frac{Y_{t+1}}{Y_t} \right) \phi_m \pi_{t+1} (1+\pi_{t+1}) $$
$$→\phi_m (\Pi_t-1) \Pi_t =(1+g)(1- \theta ) + \theta w_t + \beta \left( \frac{C_t}{C_{t+1}} \right) ^{\chi_c} \left( \frac{Y_{t+1}}{Y_t} \right) \phi_m (\Pi_{t+1}-1) \Pi_{t+1} $$
$$ヒント:\phi_m (\Pi_t-1) \Pi_t -(1+g)(1- \theta ) – \theta w_t = \beta \left( \frac{C_t}{C_{t+1}} \right) ^{\chi_c} \left( \frac{Y_{t+1}}{Y_t} \right) \phi_m (\Pi_{t+1}-1) \Pi_{t+1} $$
ここで次のように変形し、左辺=F(Π(t), w(t))、右辺=G(C(t),C(t+1),Y(t),Y(t+1),Π(t+1))とおく。なお、補助金を意味するgと関数Gがかぶってしまっているが、両者は別物である。わかりにくくて申し訳ない。特に本問はわかりにくい。
$$\phi_m (\Pi_t-1) \Pi_t -(1+g)(1- \theta ) – \theta w_t = \beta \left( \frac{C_t}{C_{t+1}} \right) ^{\chi_c} \left( \frac{Y_{t+1}}{Y_t} \right) \phi_m (\Pi_{t+1}-1) \Pi_{t+1} $$
Fについて
$$d F(\Pi_t, w_t)=\frac{\partial F(\Pi^*, w^*)}{\partial \Pi_{t}} \Pi^* d \log(\Pi_{t})$$
$$+\frac{\partial F(\Pi^*, w^*)}{\partial w_{t}} w^* d \log(w_{t})$$
$$= \phi_m (2 \Pi^* -1)\Pi^* d \log(\Pi_{t})$$
$$-\theta w^* d \log(w_{t})$$
Gについて
$$G(C_t,C_{t+1},Y_t,Y_{t+1},\Pi_{t+1})=\frac{\partial G(C^*,C^*,Y^*,Y^*,\Pi^*)}{\partial C_{t}} C^* d \log(C_{t})$$
$$+\frac{\partial G(C^*,C^*,Y^*,Y^*,\Pi^*)}{\partial C_{t+1}} C^* d \log(C_{t+1})$$
$$+\frac{\partial G(C^*,C^*,Y^*,Y^*,\Pi^*)}{\partial Y_{t}} Y^* d \log(Y_{t})$$
$$+\frac{\partial G(C^*,C^*,Y^*,Y^*,\Pi^*)}{\partial Y_{t+1}} Y^* d \log(Y_{t+1})$$
$$+\frac{\partial G(C^*,C^*,Y^*,Y^*,\Pi^*)}{\partial \Pi_{t+1}} \Pi^* d \log(\Pi_{t+1})$$
ややこしくなってきたので、ここで「ヒント」にした理由を説明したい。積と累乗だけで構成された関数FをXで微分してXをかけると、次数が前に出てきて元の関数Fが出現する関係を使う。例えば
$$F(X,Y,Z)=X^{\alpha}YZならば$$
$$\left( \frac{\partial F(X,Y,Z)}{\partial X} \right) X=\alpha X^{\alpha-1}YZX=X^{\alpha}YZ=\alpha F(X,Y,Z)$$
↑を用いると
$$\beta \left( \frac{C_t}{C_{t+1}} \right) ^{\chi_c} \left( \frac{Y_{t+1}}{Y_t} \right) \phi_m (\Pi_{t+1}-1) \Pi_{t+1} $$
$$=\chi_c G^* d \log(C_{t})$$
$$-\chi_c G^* d \log(C_{t+1})$$
$$+G^* d \log(Y_{t})$$
$$-G^* d \log(Y_{t+1})$$
$$+\beta \phi_m (2 \Pi^* -1)\Pi^* d \log(\Pi_{t+1})$$
$$=\beta \phi_m (2 \Pi^* -1)\Pi^* d \log(\Pi_{t+1})$$
dF=dGより
$$\phi_m (2 \Pi^* -1)\Pi^* d \log(\Pi_{t})-\theta w^* d \log(w_{t})$$
$$=\beta \phi_m (2 \Pi^* -1)\Pi^* d \log(\Pi_{t+1})$$
$$ここで表記を\widehat{C_t}=d \log(C_t) ≒\frac{C_t- C^*}{C^*}のようにあらためると$$
$$\phi_m (2 \Pi^* -1)\Pi^* \widehat{\Pi_{t}}-\theta w^* \widehat{w_{t}}$$
$$=\beta \phi_m (2 \Pi^* -1)\Pi^* \widehat{\Pi_{t+1}}$$
インフレ率Π*=1での定常均衡周りでの対数線形化なので、Π*=1であるから
$$\phi_m \widehat{\Pi_{t}}-\theta w^* \widehat{w_{t}}=\beta \phi_m \widehat{\Pi_{t+1}}$$
$$ \widehat{\Pi_{t}}=\beta \widehat{\Pi_{t+1}} +\frac{\theta}{\phi_m} w^* \widehat{w_{t}}+(1- \theta ) G^* \widehat{G_{t}}$$
もう少し踏み込むとインフレ率Π*=1より
$$\widehat{\Pi_{t}}=\log(1+\pi_{t})≒\pi_t$$
であるので、
$$\pi_{t}=\beta \pi_{t+1} +\frac{\theta}{\phi_m} w^* \widehat{w_{t}}+(1- \theta ) (1+g) \widehat{G}$$
さらに問9より
$$w^*=\frac{(1+g )( \theta -1)}{\theta}であるから$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{\theta}{\phi_m} \frac{(1+g )( \theta -1)}{\theta} \widehat{w_{t}}$$
$$=\beta \pi_{t+1} +\frac{(1+g )( \theta -1)}{\phi_m} \widehat{w_{t}}$$
問B-4(対数線形化) 最終財市場均衡条件
問B-4(対数線形化)次の最終財市場均衡条件をインフレ率0、自然利子率r*、最適補助金率g*の定常均衡周りで対数線形化せよ。また、対数差は上に^をつけて表現せよ。グロスインフレ率をΠ=1+πで表して計算せよ。
$$Y_{t}=C_t+\frac{\phi_m}{2} \pi_t ^2 Y_{t} $$
$$Y_{t}=C_t+\frac{\phi_m}{2} (\Pi_t-1) ^2 Y_{t} $$
ここで次のように変形し、左辺=F(Y(t),C(t),)、右辺=G(Π(t),Y(t))とおく。なお、補助金を意味するgと関数Gがかぶってしまっているが、両者は別物である。わかりにくくて申し訳ない。
$$Y_{t}-C_t=\frac{\phi_m}{2} (\Pi_t-1) ^2 Y_{t} $$
Fについて
$$d F(Y_t,C_t)=\frac{\partial G(Y^*,C^*)}{\partial Y_{t}} Y^* d \log(Y_{t})$$
$$+\frac{\partial F(Y^*,C^*)}{\partial C_{t}} C^* d \log(C_{t})$$
$$=Y^* d \log(Y_{t})- C^* d \log(C_{t})$$
Gについて
$$d G(\Pi_t,Y_t)=\frac{\partial G(\Pi^*,Y^*)}{\partial \Pi_{t}} \Pi^* d \log(\Pi_{t})$$
$$+\frac{\partial G(\Pi^*,Y^*)}{\partial Y_{t}} Y^* d \log(Y_{t})$$
$$=\frac{\phi_m}{2} 2(\Pi^*-1) \Pi^* d \log(\Pi_{t})$$
$$+\frac{\phi_m}{2} (\Pi^*-1) ^2 Y^* d \log(Y_{t})$$
ここでΠ*=1に注目して
$$d G(\Pi_t,Y_t)=0$$
dF=dGより
$$Y^* d \log(Y_{t})- C^* d \log(C_{t})=0$$
$$ここで表記を\widehat{C_t}=d \log(C_t) ≒\frac{C_t- C^*}{C^*}のようにあらためると$$
$$Y^* \widehat{Y_{t}}- C^* \widehat{C_{t}}=0$$
インフレ率π=0のとき、問9よりY*=C*になる。よって
$$\widehat{Y_{t}}= \widehat{C_{t}}$$
B-5(対数線形化) マクロ生産関数
問B-5(対数線形化)次のマクロ生産関数をインフレ率0、自然利子率r*、最適補助金率g*の定常均衡周りで対数線形化せよ。
$$Y_t=L_t$$
$$\widehat{Y_t}=\widehat{L_t}$$
問B-6(対数線形化) 対数線形化ニューケインジアン・モデル
問B-6(対数線形化) 今までの結果を用いて、対数線形化ニューケインジアン・モデルを作れ。
$$\widehat{C_t}=\widehat{C_{t+1}}-\frac{1}{\chi_C} (i_t -r^*-\pi_{t+1})$$
$$\widehat{w_t}=\chi_L \widehat{L_t}+\chi_C \widehat{C_t}$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1)}{\phi_m} \widehat{w_{t}}$$
$$ \widehat{Y_{t}}=\widehat{C_{t}}$$
$$\widehat{Y_t}=\widehat{L_t}$$
よって
$$\widehat{Y_t}=\widehat{L_t}=\widehat{C_{t}}$$
$$\widehat{w_t}=(\chi_L+\chi_C)\widehat{Y_t}$$
$$\widehat{Y_t}=\widehat{Y_{t+1}}-\frac{1}{\chi_C} (\widehat{I_{t}}-\widehat{\Pi_t})$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1)}{\phi_m} \widehat{w_{t}}$$
$$=\beta \pi_{t+1} +\frac{(1+g )( \theta -1) (\chi_L+\chi_C)}{\phi_m}\widehat{Y_t}$$
$$=\beta \pi_{t+1} +\frac{(1+g )( \theta -1)}{\phi_m} \widehat{w_{t}}$$
$$=\beta \pi_{t+1} +\frac{(1+g )( \theta -1)}{\phi_m} \widehat{w_{t}}$$
問C:対数線形近似ニューケインジアン・モデル
問C-1(対数線形近似) 対数線形近似ニューケインジアン・モデル
問C-1(対数線形近似) 対数線形近似ニューケインジアン・モデルを作れ。
(1)対数差を乖離率に近似できると解釈して、小文字に書き換えよ。ただし、グロスインフレ率、グロス利子率の対数差は乖離率と解釈せず、そのままにする。
(2)グロスインフレ率、グロス利子率の対数差を、乖離差に近似できると解釈してモデルに加えよ。なお、インフレ率の乖離差とはインフレ0との差、利子率の乖離差とは自然利子率r*との差、補助金率の乖離差とは最適補助金率g*との差である。
(1)
$$y_t=l_t=c_{t}$$
$$w_tの乖離率=(\chi_L+\chi_C) y_t ←wはすでに小文字なので日本語で補足$$
$$y_t=y_{t+1}-\frac{1}{\chi_C}(\widehat{I_{t}}-\widehat{\Pi_t})$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1) (\chi_L+\chi_C)}{\phi_m} y_t $$
(2)
ログ近似式より
$$\widehat{\Pi_{t}}=\log(\Pi_{t})-\log(\Pi^*)≒\pi_t-0=\pi_t$$
$$\widehat{I_{t}}=\log(I_{t})-\log(I^*)=\log(1+i_t)-\log(1+r^*)≒i_t-r^*$$
$$y_t=l_t=c_{t}$$
$$w_tの乖離率=(\chi_L+\chi_C) y_t$$
$$y_t=y_{t+1}-\frac{1}{\chi_C}(i_t-r^*-\pi_t)$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1) (\chi_L+\chi_C)}{\phi_m} y_t$$
問C-2(対数線形近似) 対数線形近似ニューケインジアン・モデルまとめ
問C-2(対数線形近似) 今までの議論をまとめよ。
(1)オイラー方程式、ニューケインジアン・フィリップス曲線のみ抜き出せ。
(2)次の変数を用いてまとめ直せ。
$$\sigma=\frac{1}{\chi_C}、\kappa=\frac{(1+g )( \theta -1)(\chi_L+\chi_C)}{\phi_m}$$
(解答)
(1)
$$y_t=y_{t+1}-\frac{1}{\chi_C}(i_t-r^*-\pi_t)$$
$$\pi_{t}=\beta \pi_{t+1} +\frac{(1+g )( \theta -1) (\chi_L+\chi_C)}{\phi_m} y_t$$
(2)
$$y_t=y_{t+1}-\sigma (i_t-r^*-\pi_t)$$
$$\pi_{t}=\beta \pi_{t+1} +\kappa y_t$$
問D:社会厚生
問D-1:効用関数のあれこれ
問D-1(社会厚生)家計の効用関数を社会厚生と考える。次の計算問題を解け。
$$効用関数U(C_t,L_t)=\frac{C_t^{1-\chi_C}-1}{1-\chi_C} -\frac{L_t^{1+\chi_L}}{1+\chi_L}$$
$$消費の限界効用U_{C_t}'(C_t,L_t)=\frac{\partial U_{C_t}(C_t,L_t)}{\partial C_t}=$$
$$消費の2階微分効用U_{C_t,C_t}”(C_t,L_t)=\frac{\partial}{\partial C_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =$$
$$消費、労働で微分した効用U_{C_t,L_t}”(C_t,L_t)=\frac{\partial}{\partial L_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =$$
$$労働の効用U_{L_t}'(C_t,L_t)=\frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t}=$$
$$労働の2階微分効用U_{L_t,L_t}”(C_t,L_t)=\frac{\partial}{\partial L_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =$$
$$消費の相対的リスク回避度=-\frac{C_t U_{C_t,C_t}”(C_t)}{U_{C_t}'(C_t)} =$$
$$労働の相対的リスク回避度=-\frac{L_t U_{L_t,L_t}”(L_t)}{U_{L_t}'(L_t)}=$$
(解答)
$$U_{C_t}'(C_t,L_t)=\frac{\partial U_{C_t}(C_t,L_t)}{\partial C_t}=C_t^{-\chi_C}$$
$$U_{C_t,C_t}”(C_t,L_t)=\frac{\partial}{\partial C_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =-\chi_C C_t^{-\chi_C-1}$$
$$U_{C_t,L_t}”(C_t,L_t)=\frac{\partial}{\partial L_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =0$$
$$U_{L_t}'(C_t,L_t)=\frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t}=-L_t^{\chi_L}$$
$$U_{L_t,L_t}”(C_t,L_t)=\frac{\partial}{\partial L_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =-\chi_L L_t^{\chi_L-1}$$
$$U_{L_t,C_t}”(C_t,L_t)=\frac{\partial}{\partial C_t} \left( \frac{\partial U_{L_t}(C_t,L_t)}{\partial L_t} \right) =0$$
$$相対的リスク回避度=-\frac{C_t U_{C_t,C_t}”(C_t)}{U_{C_t}'(C_t)}=-\frac{C_t (-\chi_C) C_t^{-\chi_C-1}}{ C_t^{-\chi_C} } =\chi_C$$
$$相対的リスク回避度=-\frac{L_t U_{L_t,L_t}”(L_t)}{U_{L_t}'(L_t)}=-\frac{L_t (-\chi_L) L_t^{-\chi_L-1}}{ L_t^{-\chi_L} } =-\chi_L$$
問D-2:効用関数の2次近似
問D-2(効用関数)家計の効用関数をベースに社会厚生関数を作ろう。インフレゼロの定常均衡まわりで2次のテイラー展開せよ。次を用いてよい。また、インフレゼロの定常均衡における賃金w*を用いて表せ。
(1)インフレゼロの定常均衡まわりで2次のテイラー展開せよ。
(2)定常均衡からの乖離について考え、相対的リスク回避度をうまく使って計算せよ。
(3)定常均衡からの乖離を消費の限界効用で割って、賃金w*で表せ。
(4)労働を消費とインフレ率で表して変形せよ。また、インフレ率の乖離度は0に近いので2乗や4乗は0と近似してよい。
(5)^Π^2の係数が-1/2になるように全体を割ってから整理し、適当な定数λ1やλ2をおいて計算せよ。また、インフレゼロの賃金w*は
$$w^*=\frac{(\theta-1)(1+g)}{\theta}$$
であることを明示せよ。
(6)適当に置いた変数についてメモをとっておこう。(あとで使う)
$$U(C_t,L_t)=\frac{C_t^{1-\chi_C}-1}{1-\chi_C} -\frac{L_t^{1+\chi_L}}{1+\chi_L}$$
$$f(X+a,Y+b)=f(X,Y)$$
$$+\left( a \frac{\partial f}{\partial X} +b \frac{\partial f}{\partial Y} \right) f(X,Y) $$
$$+\frac{1}{2!}\left( a \frac{\partial f}{\partial X} +b \frac{\partial f}{\partial Y} \right)^2 f(X,Y) $$
$$=f(X,Y)$$
$$+ a f(X,Y) f_X'(X,Y) +b f(X,Y) f_Y'(X,Y) $$
$$+\frac{1}{2} a f(X,Y) f_{XX}”(X,Y) + a f(X,Y) f_{XY}”(X,Y) + \frac{1}{2} b f(X,Y) f_{YY}”(X,Y)$$
なお、労働の定常均衡まわりで2次のテイラー展開は
$$\widehat{L_t} =\widehat{C_t} +\frac{\phi}{2} (\widehat{\Pi_t})^2$$
であることを用いよ。
(解答)
(1)2次のテイラー展開
効用関数をインフレゼロの定常均衡まわりでテイラー展開する。
$$U(C_t,L_t)=U(C^*,L^*) $$
$$+\widehat{C_t} C^* U_{C_t}'(C^*,L^*)+\widehat{L_t} L^* U_{L_t}'(C^*,L^*) $$
$$+ \frac{1}{2} \widehat{C_t} \widehat{C_t} C^* C^* U_{C_t,C_t}”(C^*,L^*)・・・C,C$$
$$+ \widehat{C_t} \widehat{L_t} C^* L^* U_{C_t,L_t}”(C^*,L^*)・・・C,L$$
$$+ \frac{1}{2} \widehat{L_t} \widehat{L_t} L^* L^* U_{L_t,L_t}”(C^*,L^*)・・・L,L$$
$$=U(C^*,L^*)$$
$$+\widehat{C_t} C^* U_{C_t}'(C^*,L^*)+\widehat{L_t} L^* U_{L_t}'(C^*,L^*)$$
$$+ \frac{1}{2} \widehat{C_t} \widehat{C_t} C^* C^* U_{C_t,C_t}”(C^*,L^*)・・・C,C$$
$$+ 0・・・U_{C_t,L_t}”(C^*,L^*)=0$$
$$+ \frac{1}{2} \widehat{L_t} \widehat{L_t} L^* L^* U_{L_t,L_t}”(C^*,L^*)・・・L,L$$
(2)定常均衡からの乖離について考え、相対的リスク回避度をうまく使って計算せよ。
定常均衡からの乖離は
$$U(C_t,L_t) – U(C^*,L^*)$$
$$=\widehat{C_t} C^* U_{C_t}'(C^*,L^*)+\widehat{L_t} L^* U_{L_t}'(C^*,L^*) $$
$$+\frac{1}{2} \widehat{C_t} \widehat{C_t} C^* C^* U_{C_t,C_t}”(C^*,L^*)$$
$$+ \frac{1}{2} \widehat{L_t} \widehat{L_t} L^* L^* U_{L_t,L_t}”(C^*,L^*)$$
相対的リスク回避度をうまく使うために
$$相対的リスク回避度=-\frac{1}{2} \frac{ C^* U_{C_t,C_t}”(C_t,L_t)}{U_{C_t}'(C_t,L_t)}=\chi_Cと$$
$$相対的リスク回避度=-\frac{1}{2} \frac{ C^* U_{C_t,C_t}”(C_t,L_t)}{U_{C_t}'(C_t,L_t)}=-\chi_L$$
式を整理して
$$=\widehat{C_t} C^* U_{C_t}'(C^*,L^*)+\frac{1}{2} \widehat{C_t} \widehat{C_t} C^* C^* U_{C_t,C_t}”(C^*,L^*)$$
$$+\widehat{L_t} L^* U_{L_t}'(C^*,L^*) + \frac{1}{2} \widehat{L_t} \widehat{L_t} L^* L^* U_{L_t,L_t}”(C^*,L^*)$$
$$=\widehat{C_t} C^* U_{C_t}'(C^*,L^*) +\frac{ U_{C_t}'(C^*,L^*) }{2} \frac{ C^* U_{C_t,C_t}”(C^*,L^*) }{ U_{C_t}'(C^*,L^*)} C^* (\widehat{C_t})^2 $$
$$+\widehat{L_t} L^* U_{L_t}'(C^*,L^*)+\frac{ U_{L_t}'(C^*,L^*)}{2} \frac{ L^* U_{L_t,L_t}”(C^*,L^*)}{ U_{L_t}'(C^*,L^*)} L^* (\widehat{L_t})^2 $$
ここで相対的リスク回避度を使って
$$=\widehat{C_t} C^* U_{C_t}'(C^*,L^*) +\frac{ U_{C_t}'(C^*,L^*) }{2} \chi_C C^* (\widehat{C_t})^2 $$
$$+\widehat{L_t} L^* U_{L_t}'(C^*,L^*)+\frac{ U_{L_t}'(C^*,L^*)}{2} (-\chi_L) L^* (\widehat{L_t})^2 $$
限界効用と定常均衡でくくって
$$=\left( \widehat{C_t} – \frac{1}{2} \chi_C (\widehat{C_t})^2 \right) C^* U_{C_t}'(C^*,L^*)$$
$$+\left( \widehat{L_t} + \frac{1}{2} \chi_L (\widehat{L_t})^2 \right) L^* U_{L_t}'(C^*,L^*)$$
インフレゼロの定常均衡では、Y*=L*=C*より、定常均衡との乖離は
$$U(C_t,L_t) – U(C^*,L^*)$$
$$=\left( \widehat{C_t} – \frac{1}{2} \chi_C (\widehat{C_t})^2 \right) Y^* U_{C_t}'(C^*,L^*)$$
$$+\left( \widehat{L_t} + \frac{1}{2} \chi_L (\widehat{L_t})^2 \right) Y^* U_{L_t}'(C^*,L^*)$$
(3)定常均衡からの乖離を消費の限界効用で割って、賃金w*で表せ。
社会厚生関数は序数的な大小関係のみ保存されればよいので、
$$\frac{U(C_t,L_t) – U(C^*,L^*)}{Y^* U_{C_t}'(C^*,L^*)}$$
$$= \widehat{C_t} – \frac{1}{2} \chi_C (\widehat{C_t})^2+\left( \widehat{L_t} + \frac{1}{2} \chi_L (\widehat{L_t})^2 \right) \frac{U_{L_t}'(C^*,L^*)}{U_{C_t}'(C^*,L^*)}$$
効用最大化する際は限界代替率=価格比より
$$\frac{ -U_{L_t}'(C^*,L^*)}{ U_{C_t}'(C^*,L^*)}=\frac{W^*}{P^*}=w^*$$
であるから
$$\frac{U(C_t,L_t) – U(C^*,L^*)}{Y^* U_{C_t}'(C^*,L^*)}$$
$$= \widehat{C_t} – \frac{1}{2} \chi_C (\widehat{C_t})^2+\left( \widehat{L_t} + \frac{1}{2} \chi_L (\widehat{L_t})^2 \right) w^*$$
(4)労働を消費とインフレ率で表して変形せよ。また、インフレ率の乖離度は0に近いので2乗や4乗は0と近似してよい。
問題文より
$$\widehat{L_t} =\widehat{C_t} +\frac{\phi_m}{2} (\widehat{\Pi_t})^2なので$$
$$=\left( \widehat{C_t} – \frac{\chi_C}{2} (\widehat{C_t})^2 \right)- w^* \left( \widehat{C_t} +\frac{\phi_m}{2} (\widehat{\Pi_t})^2 + \frac{\chi_L}{2} \left( \widehat{C_t} +\frac{\phi_m}{2} ( \widehat{\Pi_t} ) ^2 \right)^2 \right)$$
展開して
$$=\left( \widehat{C_t} – \frac{\chi_C}{2} (\widehat{C_t})^2 \right)- w^* \left( \widehat{C_t} +\frac{\phi_m}{2} (\widehat{\Pi_t})^2 + \frac{\chi_L}{2} \left( \widehat{C_t}^2 +\phi_m ( \widehat{\Pi_t} ) ^2 +\frac{\phi^2}{4} ( \widehat{\Pi_t} ) ^4 \right) \right)$$
0に近いインフレ率の乖離度の2乗と4乗は0に近似できるので
$$≒\left( \widehat{C_t} – \frac{1}{2} \chi_C (\widehat{C_t})^2 \right)- w^* \left( \widehat{C_t} +\frac{\phi_m}{2} (\widehat{\Pi_t})^2 + \frac{\chi_L}{2} \widehat{C_t}^2 \right)$$
整理して
$$=(1-w^*)\widehat{C_t}- \frac{1}{2} (\chi_C+\chi_L w^* ) (\widehat{C_t})^2 – \frac{ w^*}{2} \phi_m( \widehat{\Pi_t} ) ^2 $$
$$\widehat{C_t}=\widehat{Y_t}より$$
$$=(1-w^*)\widehat{Y_t}- \frac{1}{2} (\chi_C+\chi_L w^* ) (\widehat{Y_t})^2 – \frac{ w^*}{2} \phi_m( \widehat{\Pi_t} ) ^2 $$
これと社会厚生の大小関係は一致する。
(5)^Π^2の係数が-1/2になるように全体を割ってから整理し、適当な定数λ1やλ2をおいて計算せよ。また、インフレゼロの賃金w*は
$$w^*=\frac{(\theta-1)(1+g)}{\theta}$$
であることを明示せよ。
$$\frac{1}{w^*\phi_m}をかけてやり$$
$$\frac{1-w^*}{w^*\phi_m}\widehat{Y_t}- \frac{\chi_C+\chi_L w^* }{2w^*\phi_m} (\widehat{Y_t})^2 – \frac{1}{2} \widehat{\Pi_t} ^2 $$
ここで
$$\lambda_g=\frac{1-w^*}{w^*\phi_m}$$
$$=\frac{1-\frac{(\theta-1)(1+g)}{\theta}}{\frac{(\theta-1)(1+g)}{\theta} \phi_m}$$
$$=\frac{\theta-(\theta-1)(1+g)}{(\theta-1)(1+g) \phi_m}$$
$$\lambda=\frac{\chi_C+\chi_L w^* }{w^*\phi_m}$$
$$=\frac{\chi_C+\chi_L \frac{(\theta-1)(1+g)}{\theta} }{ \frac{(\theta-1)(1+g)}{\theta} \phi_m}$$
$$=\frac{\theta \chi_C+\chi_L (\theta-1)(1+g) }{(\theta-1)(1+g) \phi_m}$$
つまり、λgもλも財政政策gによって変化する。さて、
$$社会厚生=\lambda_g\widehat{Y_t}- \frac{1}{2} \widehat{\Pi_t} ^2-\frac{1}{2} \lambda \widehat{\Pi_t}^2$$
$$=- \frac{1}{2} \widehat{\Pi_t} ^2 -\frac{\lambda}{2} \widehat{Y_t}^2 -\frac{\lambda_g}{2}2\widehat{Y_t}$$
$$=- \frac{1}{2} \widehat{\Pi_t} ^2 -\frac{\lambda}{2} \left( \widehat{Y_t}- \frac{\lambda_g}{\lambda} \right)^2+\frac{\lambda }{2 } \left( \frac{\lambda_g}{ \lambda} \right)^2$$
$$=- \frac{1}{2} \left( \widehat{\Pi_t} ^2 +\lambda \left( \widehat{Y_t}- \frac{\lambda_g}{\lambda} \right)^2 \right)+\frac{\lambda }{2 } \left( \frac{\lambda_g}{ \lambda} \right)^2$$
(6)適当に置いた変数についてメモをとっておこう。(あとで使う)
$$\lambda_g=\frac{\theta-(\theta-1)(1+g)}{(\theta-1)(1+g) \phi_m}$$
$$\lambda=\frac{\theta \chi_C+\chi_L (\theta-1)(1+g) }{(\theta-1)(1+g) \phi_m}$$
$$\frac{\lambda_g}{\lambda}=\frac{\theta-(\theta-1)(1+g)}{\theta \chi_C+\chi_L (\theta-1)(1+g)}$$
問D-3:中央銀行の社会厚生関数
問D-3(社会厚生関数)前問の結果から対数線形近似ニューケインジアンモデルにおける中央銀行が認識する社会厚生関数W(y,π)を導け。なお、中央銀行は財政政策を所与として行動する。
$$y_t=\frac{Y_t-Y_{\pi^{*}=0の定常均衡}}{Y_{\pi^{*}=0の定常均衡}}≒\log(Y_t)- \log(Y_{\pi^{*}=0の定常均衡})=\widehat{Y_t}$$
$$\pi_t≒\log(1+\pi_t)=\log(\Pi_t)$$
より
$$W(y_t,\pi_t)=- \frac{1}{2} \left( \pi_t ^2 +\lambda \left( y_t- \frac{\lambda_g}{\lambda} \right)^2 \right)+\frac{\lambda }{2 } \left( \frac{\lambda_g}{ \lambda} \right)^2$$
λは財政政策gによって決まる。これを中央銀行はコントロールできないので、
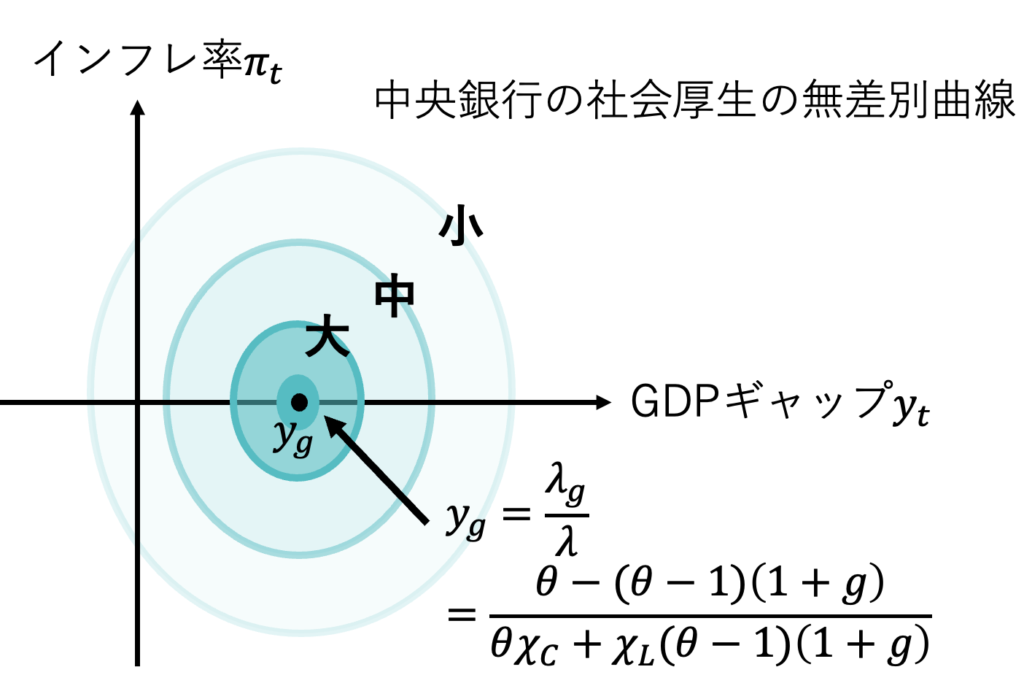
$$中央銀行の社会厚生関数W_{中央銀行}(y_t,\pi_t)$$
$$=- \frac{1}{2} \left( \pi_t ^2 +\lambda ( y_t-y_g)^2 \right) $$
$$ただし、y_g=\frac{\lambda_g}{\lambda}=\frac{\theta-(\theta-1)(1+g)}{\theta \chi_C+\chi_L (\theta-1)(1+g)}$$

問D-4:国民の社会厚生関数
問D-4:財政政策も変えられると考えたときの統合政府、国民の社会厚生関数は何か?
まず財政政策にて市場の失敗に対処し、最適財政政策を行うとする。このとき
$$g=\frac{1}{\theta-1}$$
である。すると
$$y_g=\frac{\theta-(\theta-1)(1+\frac{1}{\theta-1})}{\theta \chi_C+\chi_L (\theta-1)(1+g)}$$
$$=\frac{\theta(\theta-1)-(\theta-1)((\theta-1)+1)}{(\theta-1)\theta \chi_C+\chi_L (\theta-1)(1+g)(\theta-1)}$$
$$=\frac{\theta(\theta-1)-(\theta-1)\theta}{(\theta-1)\theta \chi_C+\chi_L (\theta-1)(1+g)(\theta-1)}$$
$$=0$$
である。ゆえに
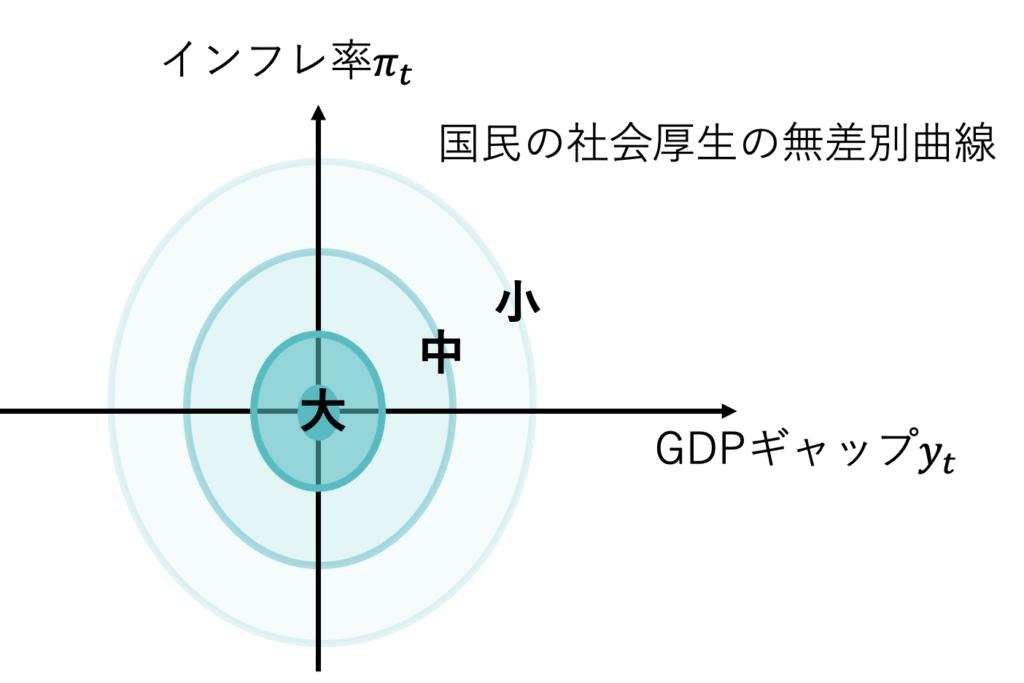
$$国民の社会厚生関数W_{国民}(y_t,\pi_t)$$
$$=- \frac{1}{2} \left( \pi_t ^2 +\lambda y_t^2 \right)$$
である。最適財政政策が行われ、余暇も労働もちょうど良く、価格調整コストを払わなくてよいのは、原点(0,0)である。

