ニューケインジアン・モデルは、景気循環や財政金融政策に関するマクロ経済モデルである。ここでは独占的競争・2次関数型価格調整コストを導入したモデルを使って議論する。
ニューケインジアン・モデルは、動学的確率的一般均衡モデル(Dynamic Stochastic General Equilibrium, DSGE)に粘着的な価格形成を導入したモデルである。ここでは、効率的な資源分配をする実現するはずの市場メカニズムが、粘着的な価格によって毀損される。その結果として、財政政策や金融政策といったケインズ政策が効果を生むようになる。
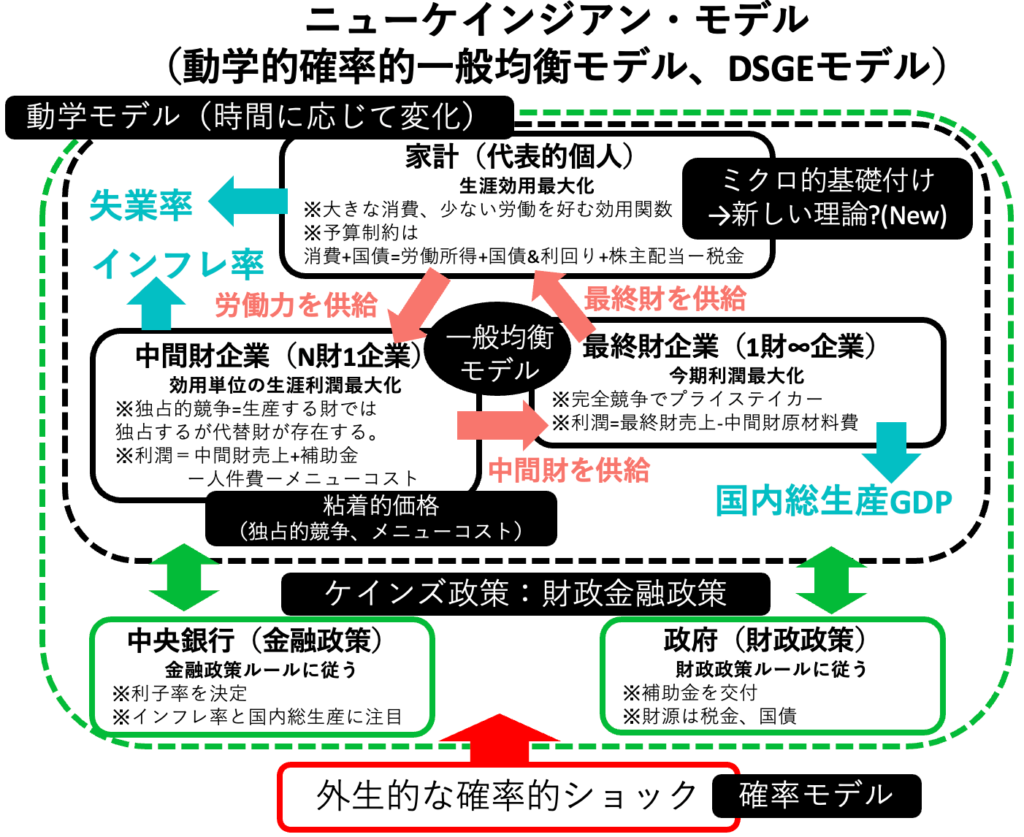
ニューケインジアン・モデルは中央銀行でも用いられているモデルであるので、学ぶ価値のあるモデルであり、経済学お勉強の一種の到達点と言える。日本銀行、FRB、欧州中央銀行もこの記事で紹介するニューケインジアン・モデルの発展形を用いている。モデルは「仲田泰祐(2020)「ゼロ金利制約下の 金融政策 FRBの政策運営」」をほんの少し変えたものを用いている。難しいところは飛ば読みしながら、生涯効用を最大化してほしい。もちろん「読まない」も最適解になりうる。ニューケインジアン・モデルの勉強時間はゼロ時間制約を抱えている。
「ニューケインジアン・モデル」解説シリーズ
企画:「しまうま総研 より良い社会のための思考法 / 3段落で簡潔明瞭」>「よりよい社会のための経済学入門」>「ニューケインジアン・モデルについて」
第1回:ニューケインジアン・モデルについて(必読 / 難易度中)
第2回:家計、最終財企業、中間財企業、市場均衡条件のミクロ的基礎について (スキップ可 / 難易度高)
第3回:非線形動学と非線形定常均衡について(スキップ可 / 難易度高)
第4回:対数線形化と対数線形近似について(スキップ可 / 難易度高)
第5回:GDPギャップとインフレの社会厚生について
第5回:テイラー・ルールと定常均衡について
第6回:中間財市場と最適財政政策について(必読 / 難易度中)
第7回:労働市場と非効率な雇用水準について
第8回:最終財市場とGDPギャップについて
第9回:独占的競争と短期なインフレについて
第10回:粘着的な価格とインフレの平準化について
第11回:最適金融政策とインフレ・バイアスについて
第12回:動学的確率的一般均衡モデルへの拡張について
第13回:Dynareを用いたシミュレーションについて
補講:DynareをMATLABで動かすための環境構築について / DynareをOctaveで動かすための環境構築について
主要な参考資料
・仲田泰祐(2020)「ゼロ金利制約下の 金融政策 FRBの政策運営」 (モデルは仲田(2020)と同じ)
・楡井誠(2023)「マクロ経済動学: 景気循環の起源の解明」
まとめ:ニューケインジアン・モデル
・家計
$$\max_{ \{ C_t,L_t,B_t \}^{\infty}_{t=1}} \sum_{t=1}^{\infty} \beta^{t-1} U(C_t,L_t)$$
$$t期の予算制約:P_t C_t + B_t =W_t L_t +(1+i_{t-1})B_{t-1}+ \Phi_t – T_t$$
$$予算制約はt=1,2 \cdots \inftyについて成り立つ。$$
$$効用関数U(C_t,L_t)=\frac{C_t^{1-\chi_C}-1}{1-\chi_C} -\frac{L_t^{1+\chi_L}}{1+\chi_L}$$
・最終財企業
$$\max_{Y_t, \{ Y_{i,t} \}^{N}_{i=1}} P_t Y_t -\sum_{i=1}^N P_{i,t} Y_{i,t}$$
$$技術制約:Y_t=\left( \frac{1}{N} \sum_{i=1}^N (NY_{i,t}) ^{\frac{\theta – 1}{\theta }} \right)^{\frac{\theta}{\theta -1}}$$
$$ただしN→ \inftyにおけるY_t=\left[ \int_{0}^{1} Y_{i,t} ^{\frac{\theta – 1}{\theta }} di\right]^{\frac{\theta}{\theta -1}}でも結果は同じ$$
・中間財企業(なお、需要制約は最終財企業の最適化行動から導ける)
$$\max_{\{ P_{i,t}, Y_{i,t},L_{i,t} \}^{N}_{i=1}} \sum_{t=1}^{\infty} \beta^{t-1} \lambda_t \left( \frac{\Phi_{i,t}}{P_t} \right)$$
$$利潤\Phi_{i,t} =P_{i,t} Y_{i,t} -W_t L_{i,t} +g P_{i,t} Y_{i,t}-\frac{\phi_m}{2} \left[ \frac{P_{i,t}}{P_{i,t-1}}-1 \right]^2 \frac{P_{t} Y_{t}}{N}$$
$$技術制約:Y_{i,t}=F_{中間}(L_{i,t})= L_{i,t}$$
$$需要制約:Y_{i,t}=\left[ \frac{P_{i,t}}{P_t} \right]^{-\theta} Y_t$$
$$技術制約、需要制約はt=1,2 \cdots \inftyについて成り立つ。$$
・政府(財政政策)
$$ 財政政策ルール:中間財企業への補助金=g P_t Y_t, G_{c,t}$$
$$予算制約: P_t T_t +B_t=g P_t Y_t + (1+i_t)B_{t} $$
・中央銀行(金融政策)
$$テイラールール:i_t=\max \left[0, r^*+ \pi_t+\phi_\pi (\pi_t-\pi^{targ}) + \phi_y y_t \right]$$
$$ただしy_t=\frac{Y_t – Y^*}{Y^*}=GDPギャップ$$
$$Y_t:実質GDP、Y^*:景気中立的実質GDP(定常均衡GDP)$$
$$\pi^{targ}:インフレ目標(インタゲ)$$
・市場均衡条件
$$最終財市場:Y_{t}=C_t+\frac{\phi_m}{2} \left[ \frac{P_{t}}{P_{t-1}}-1 \right]^2 Y_{t} $$
$$労働市場:L_{t}=\sum_{i=1}^N L_{i,t}$$
$$国債市場:B_t=B_t$$
問A:ミクロ主体の最適化行動
問1(家計) 生涯効用の最大化
問1(家計)家計の最適化問題を定式化せよ。この家計は、生涯効用を最大化する。生涯効用とは、無限期間での効用Uの割引現在価値である。ただし、期ごとに予算制約が存在する。収入は、労働所得WL、国債と利回りB(1+i)、株主配当Φを合計し、税金Tを差し引いたものである。支出は、消費額PC、政府債務購入Bの合計である。より詳しく述べる。効用関数はMaCurdy型効用関数。この家計が操作できる変数は、当期から無限期までの各期の消費C、労働L、保有政府債務Bである。逆に、この家計が操作できない変数は、物価P、利子率R、名目賃金W、中間財企の利潤Φ、税金Tである。なお、この家計はいつ外生的な確率的ショックが起きるのかを知らないが、起きたあとの経済状態の変化は決定論的に予測できる完全予見(perfect foresight)と考える。
$$\max_{ \{ C_t,L_t,B_t \}^{\infty}_{t=1}} \sum_{t=1}^{\infty} \beta^{t-1} U(C_t,L_t)$$
$$t期の予算制約:P_t C_t + B_t =W_t L_t +(1+i_{t-1})B_{t-1}+ \Phi_t – T_t$$
$$予算制約はt=1,2 \cdots \inftyについて成り立つ。$$
$$MaCurdy型効用関数U(C_t,L_t)=\frac{C_t^{1-\chi_C}-1}{1-\chi_C} -\frac{L_t^{1+\chi_L}}{1+\chi_L}$$
【内生変数(ジャンプ変数)】C:消費Consumption、L:労働Labor
【内生変数(状態変数)】B:国債Bond
【外生変数】P:最終財価格(物価)Price、W:名目賃金nominal Wage(ゆえに実質賃金w=W/P)、i:名目利子率nominal Interest rate、Φ:株主配当、T:税金Tax
【パラメーター】χc:消費の相対的リスク回避度、χL:余暇の相対的リスク回避度
問2(最終財企業) 今期利潤の最大化
問2(最終財企業)最終財企業の最適化問題を定式化せよ。この企業は、t期ごとに利潤を最大化する。利潤=最終財の売上ー中間財の仕入費用である。この企業は、t期ごとに中間財企業からN種の中間財を仕入れて、最終財を生産して、家計に販売する。また、中間財から最終財を生産する際に、労働や資本は必要ない。ただし、中間財から最終財を生産する関数は、CES型生産関数である。なお、最終財企業は完全競争に直面している。この最終財企業が操作できる変数は、当期のN種の中間財の仕入量、最終財の生産量である。逆に、この最終財企業が操作できない変数は、最終財価格と中間財価格である。
$$\max_{\{ Y_{i,t} \}^{N}_{i=1}} P_t Y_t -\sum_{i=1}^N P_{i,t} Y_{i,t}$$
$$技術制約:Y_t=F_{最終}(Y_{1,t},Y_{2,t},\cdots , Y_{i,t}, \cdots ,Y_{N,t})$$
$$=Y_t=\left( \frac{1}{N} \sum_{i=1}^N (NY_{i,t}) ^{\frac{\theta – 1}{\theta }} \right)^{\frac{\theta}{\theta -1}}・・・CES型生産関数$$
【内生変数(ジャンプ変数)】Y:最終財の生産量Yield、Yi:i中間財の仕入れ量Yield
【外生変数】P:最終財価格(物価)Price、Pi:中間財価格Price
【パラメーター】θ:代替の弾力性
$$ただしN→ \inftyにおけるY_t=\left[ \int_{0}^{1} Y_{i,t} ^{\frac{\theta – 1}{\theta }} di\right]^{\frac{\theta}{\theta -1}}でもよい$$
積分形にしなかったのは積分の微分をすることなしにモデルを理解したかったから+より現実的だから+ミクロな市場の話をしたかったからである。関数形は「楡井誠(2023)「マクロ経済動学: 景気循環の起源の解明」 」の第5章4節を用いた。
問3(中間財企業) 生涯利潤の最大化+独占的競争+メニューコスト
問3(中間財企業)中間財企業の最適化問題を定式化せよ。この企業は、効用単位に直した全期間の利潤の割引現在価値を最大化する。また、中間財企業は1つの中間財に1社しかいない独占企業である。しかし、N種の中間財が存在しており、それぞれが代替財なので、一般均衡の枠組みで競争している。この独占的競争は、現実の企業と等しい。詳しく述べよう。この企業は家計と最終財企業の最適化行動から導かれる需要関数(下の式の通り)に直面しているが、任意の中間財価格を設定できる独占的競争を行なっている。また、この中間財企業は、労働を投入し、中間財を生産する。この企業は、中間財を売り、売り上げを得る。この売り上げに応じて政府からの補助金が支給される。ここから、人件費、メニューコストを差し引く。メニューコストとは、価格改定にともなって生まれる費用であり、関数形は2次関数である(下の式の通り)。得られる貨幣的な利潤は、売り上げ+補助金ー人件費ーメニューコストであるが、これを効用単位に直す。無限期間での生涯効用最大化であるので、割引因子βで現在価値に直して、合計Σすべきである。問1の定式化より、名目ではなく実質で考えるので、物価で割ってやる。ラグランジュ関数(Λ=効用+λ予算)でのλは、貨幣単位を効用単位に変換するパラメーターであるので、それを掛けてやる。この中間財企業が操作できる変数は、当期の中間財価格Pi、中間財の生産量Yi、労働投入量Liである。逆に、この中間財企業が操作できない変数は、政府補助金τ、賃金Wである。
$$\max_{\{ P_{i,t}, Y_{i,t},L_{i,t} \}^{N}_{i=1}} \sum_{t=1}^{\infty} \beta^{t-1} \lambda_t \left( \frac{\Phi_{i,t}}{P_t} \right)$$
$$利潤\Phi_{i,t} =P_{i,t} Y_{i,t} -W_t L_{i,t} +g P_{i,t} Y_{i,t}-\frac{\phi_m}{2} \left[ \frac{P_{i,t}}{P_{i,t-1}}-1 \right]^2 \frac{P_{t} Y_{t}}{N}$$
$$技術制約:Y_{i,t}=F_{中間}(L_{i,t})= L_{i,t}・・・線形生産関数$$
$$需要制約:Y_{i,t}=\left[ \frac{P_{i,t}}{P_t} \right]^{-\theta} Y_t・・・需要曲線$$
【内生変数(ジャンプ変数)】Pi:中間財iの価格、Yi:中間財iの生産量Yi、Li:中間財i生産のための労働投入量
【外生変数】P:最終財価格(物価)Price、W:名目賃金nominal Wage、λ:貨幣の限界効用、売上補助金率τ
【パラメーター】φm:メニューコスト係数
$$【隠れた内生変数(状態変数)】このモデルを解くと$$
$$中間財値上げ率\frac{P_{i,t} – P_{i,t-1}}{P_{i,t-1}}=インフレ率\frac{P_{t} – P_{t-1}}{P_{t-1}}=\pi_t$$
$$より、実はインフレ率\pi_tが状態変数になっている。$$
$$これが粘着的価格のモデル化になっている。(問5)$$
問B:政府
問B-1(財政政策) 市場の失敗への対処
問B-1(財政政策・対GDP一定の政府支出ルール)財政政策をモデル化せよ。政府は、GDPに対して一定の割合gで補助金を拠出する政策を行うと考える。補助金政策のために、政府は税収と政府債務発行により賄う。政府債務返済は行う。ここからより詳しく述べる。政府はGDPに対して一定の割合gで、補助金を中間財企業に支出する。なお、中間財企業の利潤は家計にも分配されるので、補助金は最終的には家計に還元される。(参考:財務省「これからの日本のために財政を考える」>諸外国の支出と税収の規模)
$$ 財政政策ルール:財政支出=g P_t Y_t $$
$$予算制約: P_t T_t +B_t=g P_t Y_t + (1+i_t)B_{t} $$
・税収 +国債発行残高+新規国債発行=補助金+ 国債発行残高+国債償還費+国債利払い$$
【操作できる時間一定のパラメーター】τ:補助金率(国内総生産GDPに対する政府支出率)
【内生変数(ジャンプ変数)】T:税収
【内生変数(状態変数)】B:国債
【外生変数】P:最終財価格(物価)Price、Y:最終財生産量
問B-2(金融政策) テイラールール
問B-2(金融政策・テイラールール)金融政策をモデル化せよ。中央銀行はインフレ率から機械的に利子率を決定すると考える。テイラールールとは、国債の名目利子率を、自然利子率+インフレ率+(ターゲットインフレ率とのギャップ)×φ_π+(GDPギャップ)×φ_yで決定する金融政策ルールである。ただし、名目利子率は0を下回らないというゼロ金利制約が存在する。
$$テイラールール:i_t=\max \left[0, r^*+ \pi_t+\phi_\pi (\pi_t-\pi^{targ}) + \phi_y y_t \right]$$
$$ただしy_t=\frac{Y_t – Y^*}{Y^*}$$
$$Y_t:実質GDP、Y^*:景気中立的実質GDP(定常均衡GDP)$$
なお、max[A,B]は、AかBの大きい方の意味。
【外生変数】π:利子率、r*:自然利子率
【パラメーター】φπ:インフレ率に関するテイラールール係数、φy:GDPギャップに関するテイラールール係数
問C:市場均衡条件
問C(市場均衡)このニューケンジアン・モデルでは、すべての市場が均衡する一般均衡をモデル化している。どの市場がどのように市場均衡するか述べよ。市場均衡条件とは、金額ではなく、モノの個数が一致することである。
(解答)
・最終財市場:需要者である家計の消費需要と、中間財企業の価格調整コストを支払うための需要が存在する。完全競争の最終財企業が供給する。
・中間財市場:N種の中間財市場が存在する。各市場には供給者が1社だけおり、価格支配力を持つ。ただし、需要者である最終財企業の需要曲線は所与であり、また、他の中間財も代替財であるので他の市場の企業と競争をしている。以上を踏まえて、中間財企業が生産量を決定し、それに応じて最終財企業が仕入れする。
・労働市場:中間財企業が独占利潤を得るための生産に必要な労働を需要し、所得を得たい家計が供給する
・国債市場:家計が異時点間の最適化行動を可能にするために必要な量の国債が発行される。残りを税金で補填する。この経済には資本市場は存在しないので、国債には異時点間の最適化行動を可能にするための重要な意味が付与されている。
