情報はたくさん集めた方がいい思考ができる。インプットされる情報の質が高くて、素直な人間ならそうだろう。
一致性は、ある意味で「素直」な推定量の性質である。一致性とは、サンプル・サイズを増やした際に、推定量がパラメーターに確率収束することを意味する。nをサンンプル・サイズ、θをパラメーター、^θを推定量とすると、一致性とは次の式で表せる。また、一致性を図にて表現すると図1の赤の推定量のように表せる。赤の推定量は、サンプルサイズを増やしていくと、パラメーター80近傍の値を取る確率がどんどん増えていく。
$$任意の\epsilon >0に対して、n→∞のとき$$
$$P(|\widehat{\theta}_n -\theta|>\epsilon )=0$$
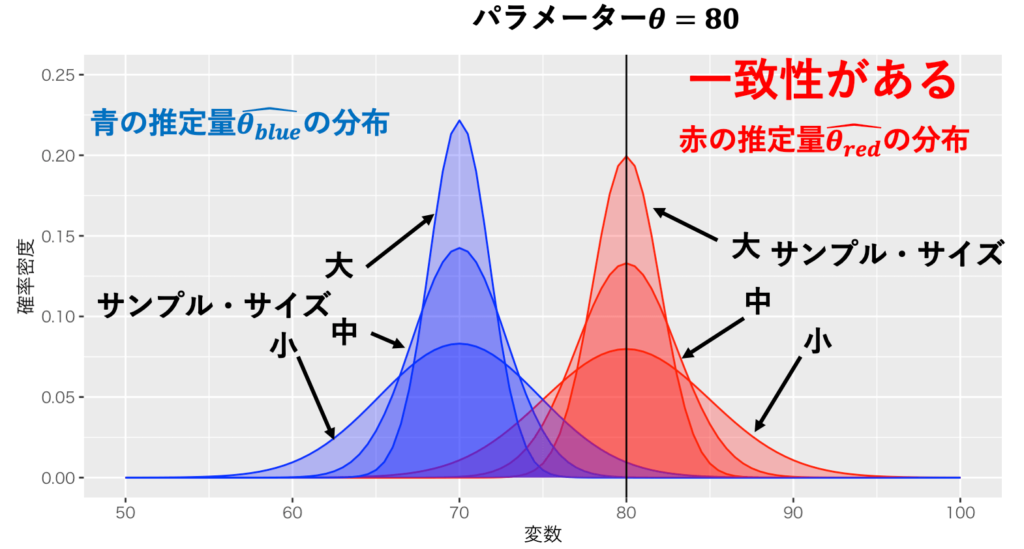
出典:しまうま総研(2023)
解説:コードは付録に掲載
こじらせている人は、いくら情報をインプットしても、正解にはたどりつかない場合がある。推定量も同じで、前提となる仮定が満たされないと、一致性を失うことがよくある。代表例は、外生性のない最小二乗法(OLS)による回帰係数である。
【追記】
一致性に関するシミュレーションでは、図2が有名だ。母平均50、母標準分散10の正規分布に従う確率変数をi個発生させて、標本平均を計算する。iは1から3000でやってみよう。要は、サンプル・サイズ1から3000までの平均を計算するということだ。その結果が図2である。標本平均は一致性を持ちそうだ。
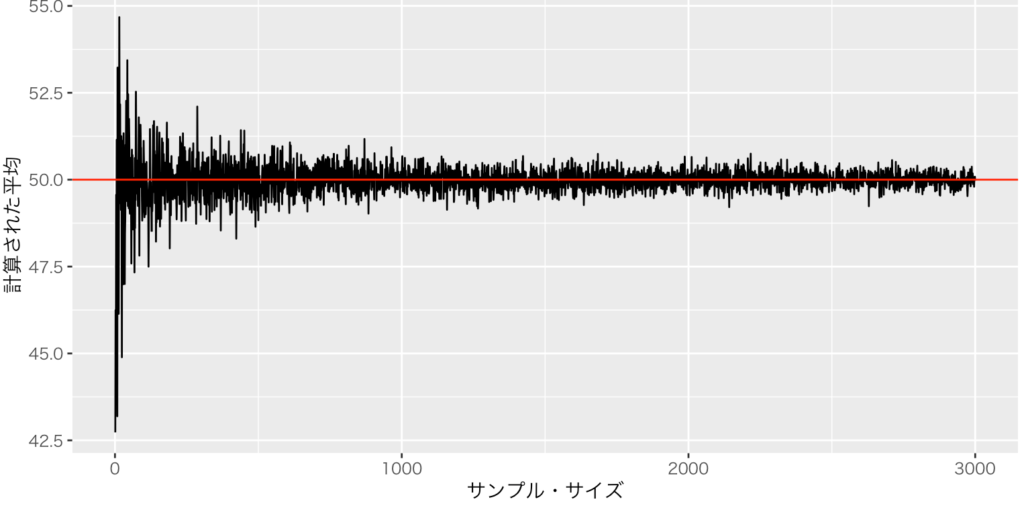
出典:しまうま総研(2023)
解説:コードは付録に掲載
図1と図2のRによる作図は次のコードで可能だ。
#図1
library(ggplot2)
ggplot(data = data.frame(X = c(50, 100)), aes(x = X))+
stat_function(fun = dnorm, args = list(mean = 80,sd = 5), color="red")+
stat_function(fun = dnorm, args = list(mean = 80,sd = 3), color="red")+
stat_function(fun = dnorm, args = list(mean = 80,sd = 2), color="red")+
stat_function(fun = dnorm, args = list(mean = 70,sd = 4.8), color="blue")+
stat_function(fun = dnorm, args = list(mean = 70,sd = 2.8), color="blue")+
stat_function(fun = dnorm, args = list(mean = 70,sd = 1.8), color="blue")+
scale_y_continuous(limits=c(0,0.25))+
xlab("変数")+
ylab("確率密度")+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=80,sd=3)), aes(x=X, ymin=0, ymax=Y),fill="red",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=80,sd=5)), aes(x=X, ymin=0, ymax=Y),fill="red",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=80,sd=2)), aes(x=X, ymin=0, ymax=Y),fill="red",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=70,sd=2.8)), aes(x=X, ymin=0, ymax=Y),fill="blue",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=70,sd=4.8)), aes(x=X, ymin=0, ymax=Y),fill="blue",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(50,100,len=101), Y=dnorm(x,mean=70,sd=1.8)), aes(x=X, ymin=0, ymax=Y),fill="blue",alpha=0.3)+
theme_grey(base_family = "HiraKakuPro-W3")+
geom_vline(xintercept =80 )
#図2
#一致性のシミュレーション
#サンプル・サイズを増やす際、全サンプルを再生成する場合
sample_size_max <- 3000 #最大のサンプル・サイズを設定(任意)
data0 <- rep(0, sample_size_max) #シミュレーション結果を入れるdata0を作成
for (i in 1:sample_size_max) { #iが1から「最大のサンプル・サイズ」になるまで繰り返し処理
x <- rnorm(i, 50, 10) #平均50、標準偏差10の正規分布に従うxをi個乱数発生
data0[i] <- mean(x) #i個のxの平均を取り、data0のi番目に格納
}
# 可視化
library(ggplot2)
ggplot() +
geom_line(aes(x = 1:sample_size_max, y = data0)) +
geom_hline(yintercept = 50, color = "red") +
xlab("サンプル・サイズ")+
ylab("計算された平均")+
theme_grey(base_family = "HiraKakuPro-W3")
#図3(本文に記載なし)
#サンプル・サイズを増やす際、過去のサンプルに一つサンプルを追加する場合
sample_size_max <- 3000 #最大のサンプル・サイズを設定(任意)
x <- rnorm(sample_size_max, 50, 10) #データを作る
data0 <- rep(0, sample_size_max) #シミュレーション結果を入れるdata0を作成
for (i in 1:sample_size_max) { #iが1から「最大のサンプル・サイズ」になるまで繰り返し処理
data0[i] <- mean(x[1:i]) #データの1番目からi番目までのxの平均を取り、data0のi番目に格納
}
# 可視化
library(ggplot2)
ggplot() +
geom_line(aes(x = 1:sample_size_max, y = data0)) +
geom_hline(yintercept = 50, color = "red") +
xlab("サンプル・サイズ")+
ylab("計算された平均")+
theme_grey(base_family = "HiraKakuPro-W3")