ヘキット・モデルについて / サンプル・セレクション・バイアスの除去

　ヘキット・モデル(Hekit model)は、標本が偏りなく観測できないことで発生するサンプル・セレクション・バイアスに対処するためのモデルだ。ヘキット・モデルでは、標本が観測されるまでは次の順序をたどる場合に使える。第一に、説明変数Xと除外変数Zが観測される。Zはセレクション式にのみ現れる変数である。第二に、①のセレクション式（プロビット・モデル）の真偽によって、目的変数Yの観測の有無が決まる。第三に、観測ができる目的変数Yについては、構造式（重回帰モデル）にしたがって観測される。

$$①　\delta_0+\delta_0 X_1+ \cdots + \delta X_k +\delta_{k+1}Z_1+\cdots + \delta_{k+m}Z_m + U_{セレク}　>0について$$

$$真なら目的変数Yが観測され、偽なら目的変数Yが観測されない$$

$$②　Y=\beta_0 + \beta_1 X_1 +\cdots \beta_k X_k + U_{構造}$$

ただし

$$U_{セレク}は外生性をもち、標準正規分布に従う$$

$$U_{構造}は外生性をもつ$$

$$U_{セレク}= \gamma U_{構造} + 外生性をもつ誤差項$$

　

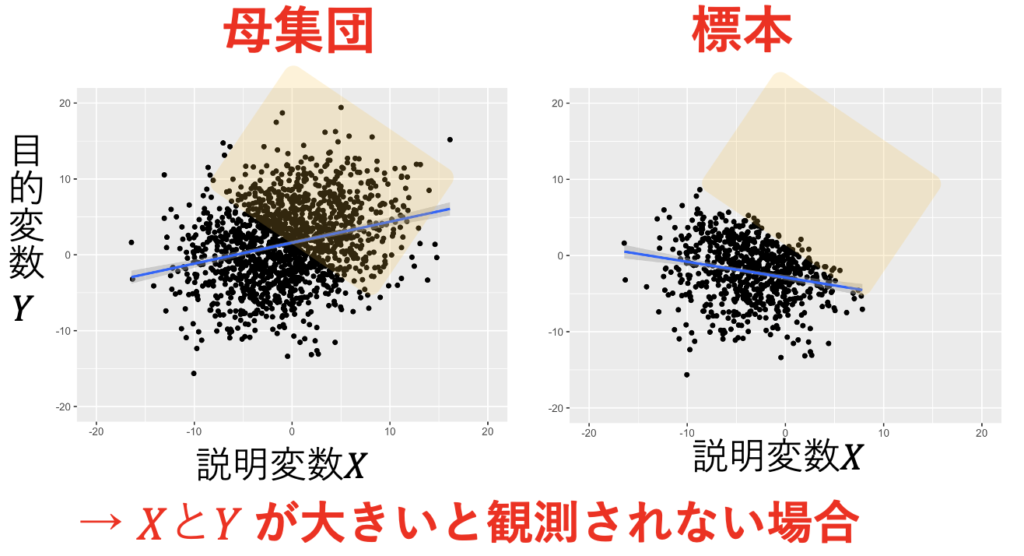
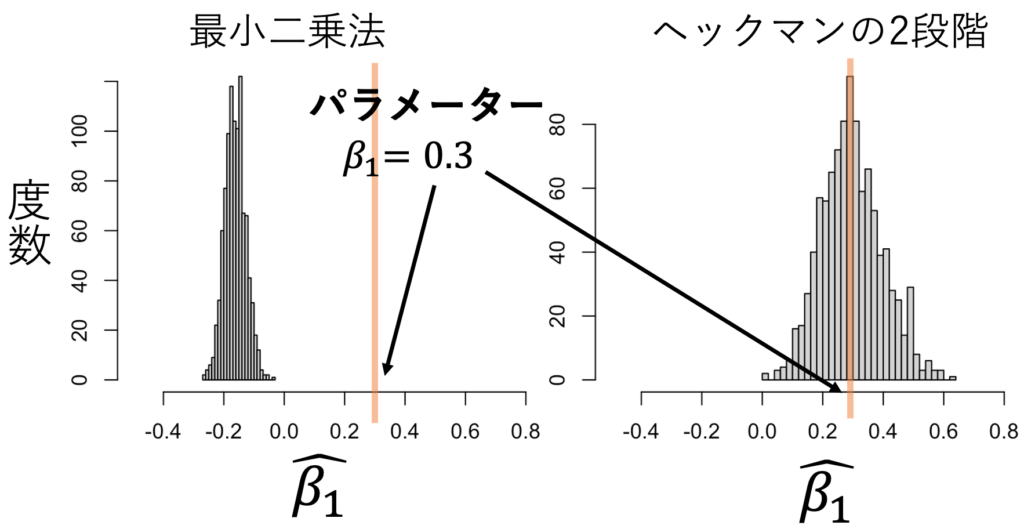
　ヘキット・モデルのパラメーター推定には、ヘックマンの二段階推定が有名だ。シミュレーションしてみよう。セレクション式、構造式、誤差項の関係は次の式で設定した。その結果、図１のようにXが大きいとYが観測されにくくなる標本の作成に成功した。本来は、図1の左のようになるはずが、サンプル・セレクションによって図１の右のようになってしまう。これを最小二乗法で推定したのが表1であり、β1=0.3であるのに、-0.2と推定している。一方で、ヘックマンの二段階法で推定したのが表2であり、β1=0.3であるところを、0.2と推定している。図2では、標本生成と推定を1000回繰り返して、推定値の分布を調べた。その結果、ヘックマンの二段階推定がうまく機能していることがわかる。

$$セレクション式　-0.1-0.2X +0.1 Z+U_{セレク} >0$$

$$構造式　Y=1.5+0.3X+U_{構造}$$

$$U_{セレク}= -5 U_{構造} + 外生性をもつ誤差項$$

　ヘキット・モデルは、結果Yについては観測できない標本もあるが、原因Xやその他の変数Zは観測できる場合に使うことができる。例えば「Y=女性の賃金(専業主婦だと観測できない)、X=女性の教育年数」「Y=大学入試点数(高卒だと観測できない)、X=中学での勉強時間」「Y=負債比率(倒産だと観測できない)、X=経営行動」といったものである。

　

【追記】

・Rコードについて：ヘックマンの二段階推定は次のコードで実行できる。

library(sampleSelection) #パッケージの呼び出し
heckit(s ~ x + z, #セレクション式
       y ~ x,  #構造式
       method = "2step", 　#2段階推定。"mls"だと最尤法で推定できる
       data=データフレーム名) 

・サンプル・セレクション・バイアスについて：

$$U_{選択}= \gamma U_{出力} + 外生性をもつ誤差項$$

におけるγが非常に重要だ。ヘキット・モデルでは、次のようになることがわかっている。

$$潜在変数　Y=\beta_0 + \beta_1 X_1 +\cdots \beta_k X_k + U_{出力}$$

$$観測　Y=\beta_0+\beta_1X+\cdots \beta_k X_k+\gamma 逆ミルズ比+\epsilon$$

　したがって、γ≠0で逆ミルズ比を入れないと欠落変数バイアスがおきるのが、サンプル・セレクション・バイアスの正体だったのである。

・逆ミルズ比について：

　逆ミルズ比とは、確率密度÷累積分布で表されるものだ。ヘキット・モデルにおける逆ミルズ比は

$$逆ミルズ比=\frac{\phi(c)}{1-\Phi(c)}=E( v|v≧c)$$

$$\phi(c)：v=cにおける標準正規分布の確率密度$$

$$\Phi(c)：v=cまでの標準正規分布の累積分布$$

である。つまり、ヘキット・モデルでは、標準正規分布に従うvがc以上のときのvの期待値を、逆ミルズ比捉えられる。

$$v　〜　N(0,1)$$

$$逆ミルズ比=E( v|v≧c)$$

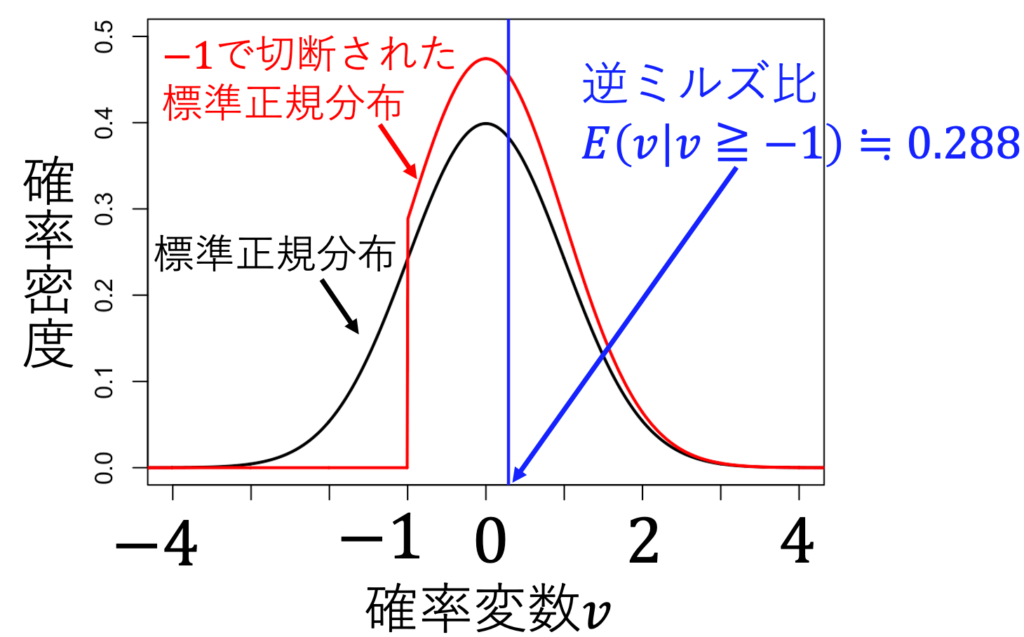
　例えば、c=-1のとき、-1以下の値を取らないvの分布は赤になる。計算すると、このときの逆ミルズ比は約0.288になる。

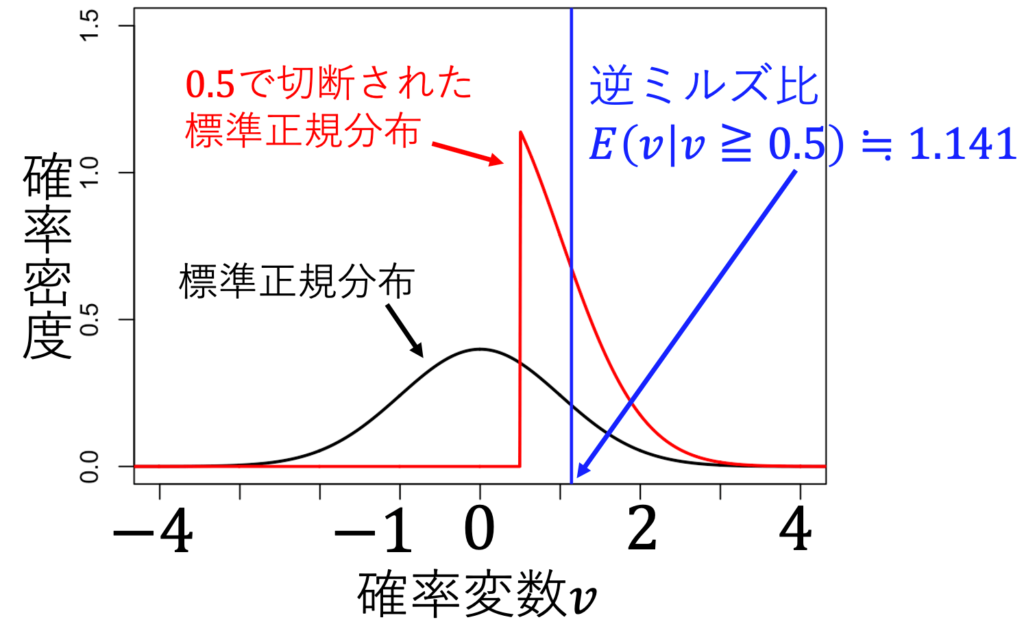
　c=0.5のとき、0.5以下の値を取らないvの分布は赤になる。計算すると、このときの逆ミルズ比は約1.141になる。

・なぜ標本でのモデルで逆ミルズ比が出てくるのかについて：

　説明変数が一つのヘキット・モデルで説明しよう。観測されるYの期待値が

$$E(Y|X,S=1)　=　\beta_0+\beta_1X+\gamma E( v|v≧c)$$

であることを説明する。Yが観測されることをS=1としよう。まず、X、S=1のときのYの条件付き期待値は

$$E(Y|X,S=1)　=　\beta_0+\beta_X+E(u|X, S=1)$$

　uとXは独立なので

$$E(Y|X,S=1)　=　\beta_0+\beta_X+E(u|S=1)$$

　S=1の条件を潜在変数モデルにしたがって言い換えると

$$=\beta_0+\beta_1X+E(u|　\delta_0+\delta_1X +\delta_2 Z+v≧0)$$

　移項して

$$=\beta_0+\beta_1X+E(u|　v≧-\delta_0-\delta_1X -\delta_2 Z)$$

　誤差項vの条件がついたuの期待値はγvと仮定しており、vにも条件がついていることを考慮すると

$$=\beta_0+\beta_1X+\gamma E( v|　v≧-\delta_0-\delta_1X -\delta_2 Z)$$

です。ここで

$$c=-\delta_0-\delta_1X -\delta_2 Z$$

とおくと

$$=\beta_0+\beta_1X+\gamma E( v|v≧c)$$

になる。この最後の項が逆ミルズ比だ。

　最後に逆ミルズ比がでてくるのは、サンプル・セレクションによってXと相関する誤差項が生まれてしまったからである。相関する誤差項を取り除いた新しい誤差項がεだ。

$$Y_{観測有}=\beta_0+\beta_1X+\gamma E( v|v≧c)+\epsilon$$

・描画と推定のRコードは以下の通り。

#サンプルの生成
sample_size <- 1500
x <- rnorm(n=sample_size, mean =-0.5, sd=5)
e <- rnorm(n=sample_size, mean =0, sd=2)
ee <- rnorm(n=sample_size, mean =0, sd=0.5)
uu <- rnorm(n=sample_size, mean =0, sd=1)
z <- -0.05 - 0.1*x + e #セレクション式1/3
ss <- -0.1 -  0.2*x + 0.1 *z+ uu #セレクション式2/3
s <- ifelse(ss>=0,1,0) #セレクション式3/3
u <- -5*uu + ee #構造式1/2
y <- 1.5 + 0.3*x + u #構造式2/2
ys <- s*(1.5 + 0.3*x + u) #サンプル・セレクション1/2
YS <- ifelse(ys==0,NA,ys) #サンプル・セレクション2/2
Data <- data.frame(x,z,y,YS)
　
#図1
library(ggplot2)
ggplot(Data,aes(x =x, y=y))+
  geom_point()+
  stat_smooth(method = "lm", se = FALSE)+
  scale_x_continuous(limits = c(-25, 25))+
  scale_y_continuous(limits = c(-20, 20))
　
ggplot(Data,aes(x =x, y=YS))+
  geom_point()+
  stat_smooth(method = "lm", se = FALSE)+
  scale_x_continuous(limits = c(-25, 25))+
  scale_y_continuous(limits = c(-20, 20))
  
#最小二乗法(表1)
lm000 <-lm(YS ~ x,data=Data)
summary(lm000) #表1
　
##ヘックマンの2段階推定(表2)
library(sampleSelection)
lm0 <- heckit(s ~ x + z, #セレクション式
              y ~ x,  #構造式
              method = "2step", 　#2段階推定。"mls"だと最尤法で推定できる
              data=Data) 
summary(lm0) #表2
　
#推定量の分布を調べる（図2）
sample_size <- 1500
trial_number <- 1000
beta_1_heck_2step <- rep(NA, trial_number)
beta_1_heck_mls <- rep(NA, trial_number)
beta_1_ols <- rep(NA, trial_number)
for(i in 1:trial_number){
  sample_number <- 1500
  x <- rnorm(n=sample_size, mean =-0.5, sd=5)
  e <- rnorm(n=sample_size, mean =0, sd=2)
  ee <- rnorm(n=sample_size, mean =0, sd=0.5)
  uu <- rnorm(n=sample_size, mean =0, sd=1)
  
  #セレクション式
  z <- -0.05 - 0.1*x + e
  ss <- -0.1 -  0.2*x + 0.1 *z+ uu
  s <- ifelse(ss>=0,1,0)
  
  #構造式
  u <- -5*uu + ee
  y <- 1.5 + 0.3*x + u
  
  #サンプル・セレクション
  ys <- s*(1.5 + 0.3*x + u)
  YS <- ifelse(ys==0,NA,ys)
  
  #ヘックマンの2段階推定
  lm0 <- heckit(s ~ x + z, 
                YS ~ x, 
                method = "2step") 
  beta_1_heck_2step[i] <- lm0$coef[5]　
  
  #最尤法
  lm00 <- heckit(s ~ x + z, 
                 YS ~ x, 
                 method = "mls") 
  beta_1_heck_mls[i] <- lm00$estimate[5]　
  
  #最小二乗推定量
  lm000 <-lm(YS ~ x)
  beta_1_ols[i] <- lm000$coef[2]
}
　
#最小二乗推定量の分布 （図2）
hist(beta_1_ols,xlim=c(-0.5,0.8),breaks=30) 
　
#ヘックマンの2段階推定の分布 （図2）
hist(beta_1_heck_2step,xlim=c(-0.5,0.8),breaks=30)
　
#最尤推定量の分布
hist(beta_1_heck_mls,xlim=c(-0.5,0.8),breaks=30)
　
#図3、図4
#打ち切り点を-1に設定
c <- -1 #打ち切り点を-1に設定、0.5なら図4
x <- seq(-5,5,length=1000)
plot(x, dnorm(x, mean=0, sd=1),  #横軸にx、縦軸に標準正規分布の確率密度
  type="l",　#折れ線グラフ
  lwd=2,　#線の太さを2
  xlim=c(-4,4),  #横軸を-4から4に
  ylim=c(0,0.5),  #縦軸を0から0.5に
  xaxp=c(-4,4,8))  #横軸を-4から4までを8つに分けて目盛りをつける
　
lines(x, dtruncnorm(x, a=c, mean=0, sd=1), type="l", col="red",lwd=2) #打ち切り標準正規分布の確率密度を描画
　
M <- dnorm(c,mean=0,sd=1)/(1-pnorm(c,mean=0,sd=1))　##逆ミルズ比を求める
　
abline(v=M,col="blue",lwd=2) #逆ミルズ比を描画