中心極限定理によれば、平均は正規分布に従う。本当だろうか。モンテカルロ・シミュレーションしてみよう。
10万個のXの平均を題材にする。Xはコンピューターで自由に作り出すことができる。Xは30、50、70近辺の値を取ることが多いと設定し、生成した。ヒストグラムにすると、変数Xは3つの山を持っている三峰型の分布である(図1)。この10万個のXから5000個をランダムに選び取り、平均を計算する。この計算を1万回繰り返す。こうして得られた1万個の平均(ピンク)を中心極限定理が予想する分布(黒)と比較する。その結果、ピッタリ一致した(図2)。中心極限定理の通りに、平均は正規分布に従った。
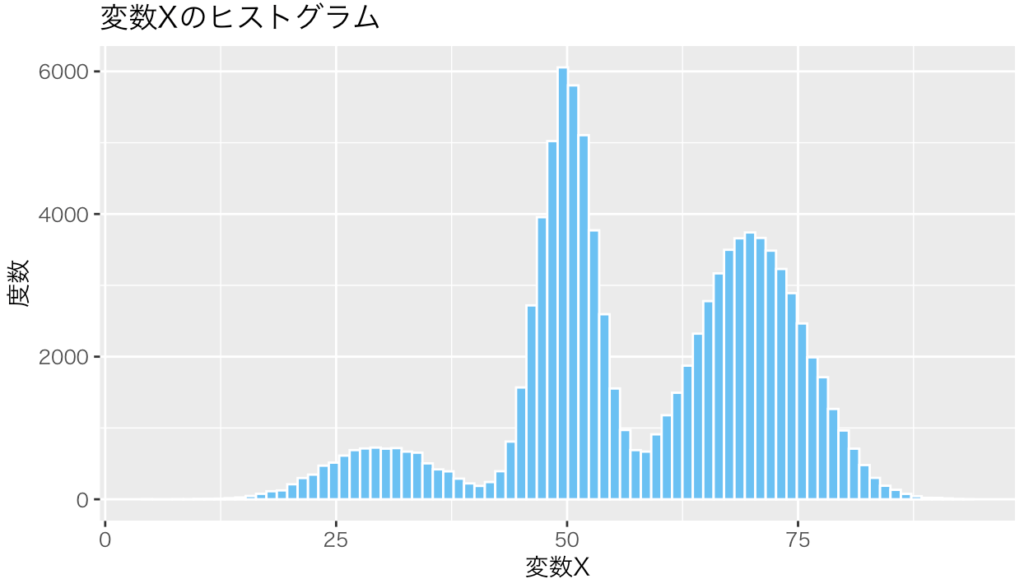
出典:しまうま総研(2023)
解説:コードは付録に掲載
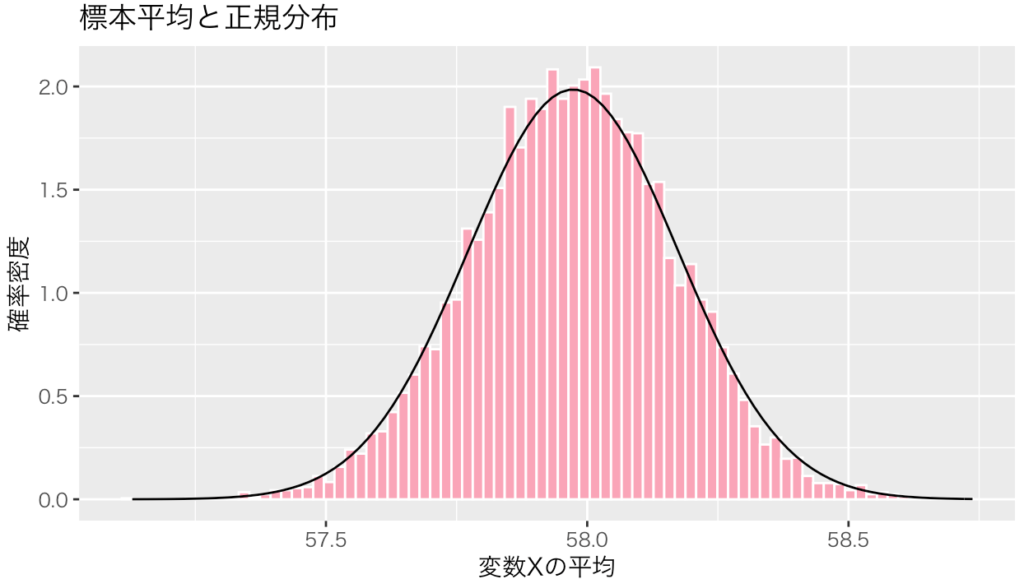
出典:しまうま総研(2023)
解説:コードは付録に掲載
中心極限定理は、統計学の土台となる。中心極限定理を用いれば、統計の基本である平均についての仮説検定が可能となるからだ。例えば、平均が0であることを仮定して、平均が従う正規分布を予想する。実際に計算された平均が、平均0であり得る範囲とかけ離れていれば、平均は0ではない。こういった推測が可能になる。
【追記】
・中心極限定理(Central limit theorem)は正確には次の定理である。
$$母平均\mu、母分散\sigma^2(有限)の$$
$$同一の母集団分布に独立に従う$$
$$n個の確率変数Xの平均\overline{X}=\frac{1}{n}\sum_{i=1}^n X_i$$
$$の分布は、母平均μ、母分散\frac{\sigma^2}{n}の大略正規分布$$
$$N \left(\mu, \sqrt{\frac{\sigma^2}{n}} \right)に従う$$
$$ただし、nは十分に大きい$$
・シミュレーションは、Rを用いて実行した。
#母集団サイズ10万の母集団を生成する
population_size <- 100000
x <- rep(NA, population_size)
for(i in 1:population_size){
x[i] <- ifelse(i < 10000,rnorm(1,30,6) ,
ifelse(i < 50000, rnorm(1,50,3),rnorm(1,70,6)))
}
data0 <- data.frame(x)
#標本を1万回生成し、標本平均を1万回計算する
trial_number <- 10000
sample_size <- 5000
mean_0 <- rep(0, trial_number)
for(i in 1:trial_number){
s <- sample(data0$x, sample_size, replace = FALSE) #無作為抽出
mean_0[i] <- mean(s) #平均の計算
}
data00 <- data.frame(mean_0)
#ggplot2によってヒストグラムを作図する
#パッケージの呼び出し。
library(ggplot2)
#母集団の分布
ggplot(data0, aes( x = x )) +
geom_histogram(bins=80,colour="white", fill = "skyblue2")+
xlab("変数X") +
ylab ("度数") +
ggtitle ("変数Xのヒストグラム") +
theme_grey(base_family = "HiraKakuPro-W3")
#標本平均の分布
ggplot(data00, aes( x = mean_0)) +
geom_histogram( bins=80,aes( y = ..density.. ),colour="white", fill = "pink2")+
stat_function(fun = dnorm, args=list(mean=mean(data0$x), sd=sqrt((var(data0$x))/sample_size)))+
xlab("変数Xの平均") +
ylab ("確率密度") +
ggtitle ("平均のヒストグラムと正規分布") +
theme_grey(base_family = "HiraKakuPro-W3")