「労働者であろうと資本家であろうと、貢献の質と量で公平に評価され、分配されると、総産出は分配し尽くされる」という完全分配定理がソロー・モデルにて成り立つ。これは規模に対して収穫一定の生産関数(一次同次の関数)(追記)を用いているからである。労働の所有者には労働の限界生産性と労働量に応じた所得が与えられ、資本の所有者には資本の限界生産性と資本量に応じた所得が与えると、国内総生産GDPはすべて分配される。しかし、資本の所有者は、固定資本減耗を負担しなければならない。資本の所有者に最終的に与えられる分配は、rKのみである。
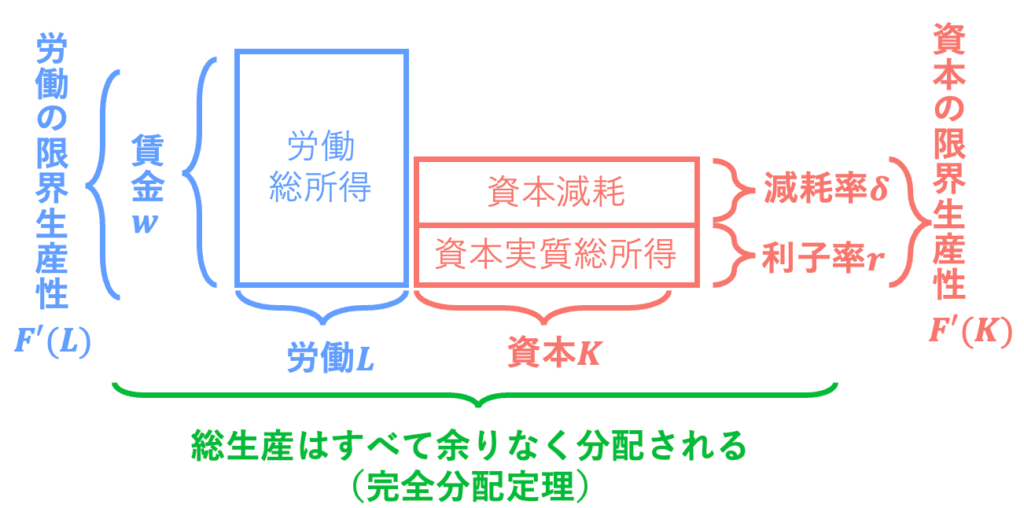
上の完全分配定理だが、固定資本減耗が入ってくることで、国内総生産が完全に分配されているわけではないのが少し引っかかる。ここでちょっと面白い見方をしてみよう。固定資本減耗とはなんだろうか。それは故障、設備の摩耗、陳腐化であるが、これは自然現象によって価値が奪われていることに他ならない。ならその価値は誰が受け取るのか? 自然現象の所有者は「神」である。つまり、資本の「機能」は資本家が保有し、「物理的実体」は神が保有するとすれば、次のように解釈できる。
$$Y_t=w_t L_t+r_tK_t+\delta K_t$$
$$=労働への分配+資本への分配+神への分配$$
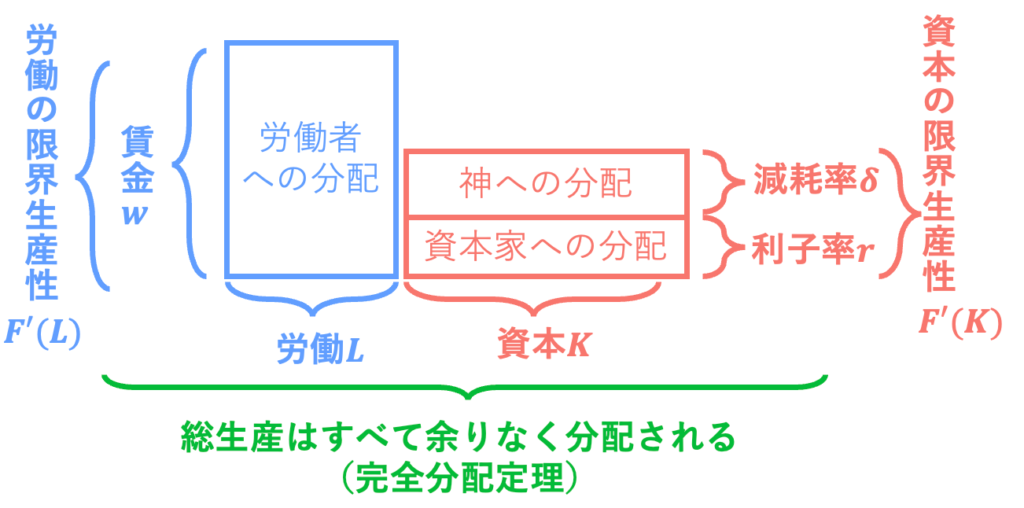
国内総生産GDPについての完全分配定理は、農業社会から脱して高度な産業社会を築いた人類も、「神」や「自然現象」からの恵みを受けていることを意味する。神は価値を与えるが、価値を奪いもするのは、ジブリ映画で描かれる「神」のようでよい。固定資本減耗を神に対する報酬と考えるのは、我ながら面白い解釈だ。
【追記:概念】
・規模に対して収穫一定の生産関数とは、一次同次の関数である。数式では
$$F(\alpha K_t,\alpha A_t L_t)=\alpha F( K_t, A_t L_t)$$
と書ける。これは資本が2倍、労働が2倍になれば、生産量が2倍になるという関数である。工場が2倍、労働者が2倍になれば、生産量が2倍になるというのは受け入れやすい仮定である。
【追記:問題】
問1:規模に対して収穫一定の生産関数は次の式が成り立つ。両辺をαで微分しても等しいことを利用して、完全分配定理を証明する。右辺をαで微分せよ。そしてそれを解釈せよ。
$$F(\alpha K_t,\alpha A_t L_t)=\alpha F( K_t, A_t L_t)・・・式1$$
$$ただし\alpha>0$$
問2:式1の左辺をαで微分せよ。次の合成関数の微分公式を用いてよい。
$$\frac{\partial f \left[ x(t),y(t) \right] }{\partial t}=\frac{\partial f \left[ x(t),y(t) \right] }{\partial x(t)}\frac{\partial x(t)}{\partial t}+\frac{\partial f \left[ x(t),y(t) \right] }{\partial y(t)}\frac{\partial y(t)}{\partial t}$$
問3:0より大きい任意のαについて式1が成り立つ。問2の結果にα=1を代入して、整理せよ。
問4:完全分配定理を導け。企業の利潤最大化から導ける次の2式を用いて、左辺の微分=右辺の微分の式に反映させよ。企業の利潤最大化から導ける次の2式は「資本所得と労働所得の成長について」の問1を確認せよ。
$$r_t=\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – \delta$$
$$w_t=\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} $$
【追記:解答】
問1:規模に対して収穫一定の生産関数は次の式が成り立つ。両辺をαで微分しても等しいことを利用して、完全分配定理を証明する。右辺をαで微分せよ。そしてそれを解釈せよ。
$$F(\alpha K_t,\alpha A_t L_t)=\alpha F( K_t, A_t L_t)・・・式1$$
$$ただし\alpha>0$$
$$右辺の微分=F( K_t, A_t L_t)=Y_t=国内総生産GDP$$
問2:式1の左辺をαで微分せよ。次の合成関数の微分公式を用いてよい。
$$\frac{\partial f \left[ x(t),y(t) \right] }{\partial t}=\frac{\partial f \left[ x(t),y(t) \right] }{\partial x(t)}\frac{\partial x(t)}{\partial t}+\frac{\partial f \left[ x(t),y(t) \right] }{\partial y(t)}\frac{\partial y(t)}{\partial t}$$
$$左辺については合成関数の微分公式を用いる$$
$$K(\alpha)=\alpha K_t, AL(\alpha)=\alpha A_t L_tとすると$$
$$左辺の微分=\frac{\partial F \left[ K(\alpha),AL(\alpha) \right] }{\partial K(\alpha)}\frac{\partial K(\alpha)}{\partial \alpha}+\frac{\partial F \left[ K(\alpha),AL(\alpha) \right] }{\partial AL(\alpha)}\frac{\partial AL(\alpha)}{\partial \alpha}$$
$$=\frac{\partial F ( \cdots ) }{\partial K(\alpha)}K_t+\frac{\partial F ( \cdots ) }{\partial AL(\alpha)}A_t L_t$$
問3:0より大きい任意のαについて式1が成り立つ。問2の結果にα=1を代入して、整理せよ。
$$ \alpha=1を代入すると$$
$$左辺の微分=\frac{\partial F (K_t,A_t L_t) }{\partial K_t}K_t+\frac{\partial F (K_t,A_t L_t) }{\partial A_t L_t}A_t L_t$$
$$=\frac{\partial F (K_t,A_t L_t) }{\partial K_t}K_t+\frac{\partial F (K_t,A_t L_t) }{\partial L_t} \frac{\partial L_t }{\partial A_t L_t} A_t L_t$$
$$=\frac{\partial F (K_t,A_t L_t) }{\partial K_t}K_t+\frac{\partial F (K_t,A_t L_t) }{\partial L_t} \frac{\partial \frac{A_t L_t }{A_t}}{\partial A_t L_t} A_t L_t$$
$$=\frac{\partial F (K_t,A_t L_t) }{\partial K_t}K_t+\frac{\partial F (K_t,A_t L_t) }{\partial L_t} L_t$$
問4:企業の利潤最大化から導ける次の2式を用いて、左辺の微分=右辺の微分の式に反映させよ。企業の利潤最大化から導ける次の2式は「資本所得と労働所得の成長について」の問1を確認せよ。
$$r_t=\frac{\partial F(K_t,A_t L_t) }{ \partial K_t} – \delta$$
$$w_t=\frac{\partial F(K_t,A_t L_t) }{ \partial L_t} $$
$$左辺の微分=右辺の微分より$$
$$\frac{\partial F (K_t,A_t L_t) }{\partial K_t}K_t+\frac{\partial F (K_t,A_t L_t) }{\partial L_t} L_t = F( K_t, A_t L_t)$$
$$(r_t+\delta)K_t+w_t L_t=Y_t$$
$$Y_t=w_t L_t+r_t K_t+\delta K_t$$
$$Y_t-\delta K_t=r_t K+w_t L_t$$
