外生性(exogeneity)は回帰モデルで最も重要な仮定だ。外生性とは、誤差項と説明変数が無相関であることを意味する。より正確には、外生性とはk種の説明変数Xで条件付けられた誤差項Uの期待値が0である。
$$モデル Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k+U$$
$$外生性 E(U|X_1,X_2 \cdots X_k)=0$$
統計モデルの究極的な目標は、目的変数Yの母集団分布の推定だが、それは難しい。なぜなら、確率分布の特定は、1次のモーメントである期待値、(期待値周りの)2次のモーメントである分散、(期待値周りの)3次のモーメントである歪度などの、すべての次数のモーメントを推定することを意味するからだ。それは不可能だ。そこで、データ分析者は、せめて1次のモーメントである期待値の予測はやりましょうと考える。これでも、モデルの外でXが決まれば、モデルの内でYの期待値が決定するので意義深い。
$$Y=f(X)+U$$
$$U:モデルf(X)では予測できない誤差項$$
$$究極的な目標 Y|Xの分布推定 $$
$$現実的な目標 E(Y|X)の推定$$
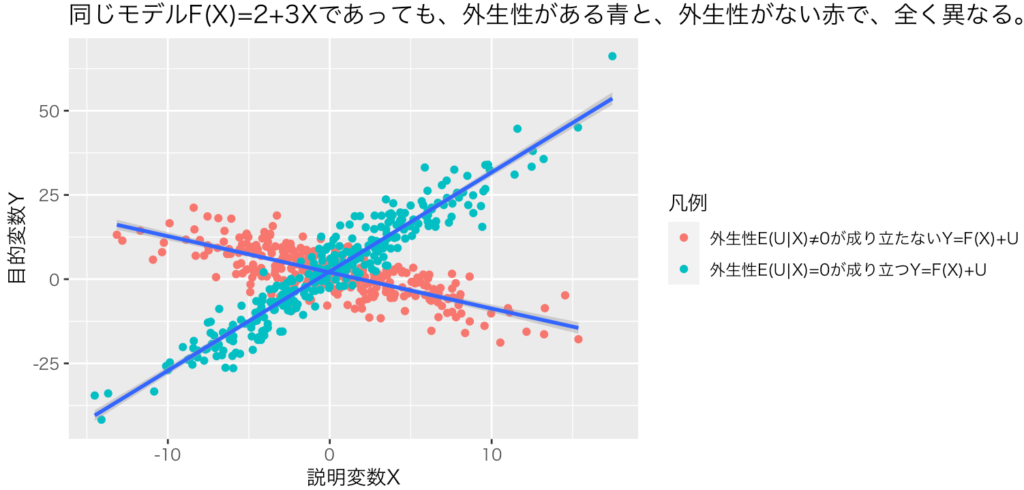
データ分析者にとって最低限の目標を実現するために、外生性が必要だ。以下の数式からわかる通り、誤差項Uと説明変数Xが相関するモデルを選んだ場合、目的変数Yの条件付き期待値の予測ができない。外生性が成り立たないと、すべての次数のモーメントどころか、1次のモーメントの推定すらできない。
$$E(Y|X)$$
$$=E \big[f(X )+U \big| X \big]$$
$$ =f(X ) +E[U|X]$$
$$もし外生性E[U|X]=0なら、期待値の予測ができる。$$
$$もし内生性E[U|X]≠0なら、期待値の予測ができない。$$
本文は以上。以下は付録。
執筆の目的
外生性は、重回帰分析における重要な仮定であるので、執筆した。
平均的に正しい予測をするためには「モデルf(X)が正しい」に加えて「モデル内にある原因Xとモデル外で発生する原因Uが、無関係である必要がある」という知見は興味深い。
問1:最小二乗推定量の不偏性、一致性
計量経済学において外生性は非常に重要視される仮定であるが、それはYの予測ではなく、βの推定において重視される。
問1:計量経済学において外生性が重要な理由は何か。
計量経済学では、重回帰モデルの回帰係数βの推定を目的をすることが多い。しかし、外生性が満たされない場合、最小二乗推定量は小さなサンプル・サイズにおいても、非常に大きなサンプル・サイズにおいてもバイアスを持つ。
ゆえに、計量経済学では、推定において外生性が成り立つか否かを非常に重要視する。外生性を含む以下の1から4の仮定が満たされると、最小二乗推定量は不偏性と一致性を持つ。詳しくは「最小二乗推定量の不偏性・一致性・漸近正規性について / 重回帰分析」をご覧頂きたい。

問2:外生性のシミュレーション
本文で掲載した画像の生成方法が気になる人向けに、プログラミングについても付記しておいた。
問2:本文の画像1のようなシミュレーションはどのように実行したのか。
画像1は、R言語を用いたモンテカルロ・シミュレーションによって作成した。具体的なコードは以下の通り。
#(必要な人のみ)パッケージのインストール
install.packages("ggplot2")
#シミュレーション者が設定するパラメーター
e <- -4 #外生性、内生性に関するパラメーター
#データの作成
sample_size <- 600 #サンプル・サイズ
pattern <- c(rep(c(1:0),c(rep(300,2)))) #1を300個、0を300個並べる
Category <- c(rep(c("A","B"),c(rep(300,2)))) #Aを300個、Bを300個並べる
X <- rnorm(n=sample_size, mean =0, sd=5) #説明変数X
U0 <- rnorm(n=sample_size, mean =0, sd=5) #外生性のある誤差項
U1 <- U0 + pattern*e*X #誤差項と説明変数Xを相関させる操作
Y <- 2+3*X+U1 #目的変数Yの生成
Data1 <-data.frame(X, Y,pattern,Category) #データフレーム化
#綺麗な散布図の描画のためのパッケージ起動
library(ggplot2)
#散布図の描画
ggplot(Data1,aes(x =X, y=Y,stat=Category))+
geom_point(aes(colour=Category))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
labs(color = "凡例")+
scale_color_hue(name = "凡例", labels = c(A = "外生性E(U|X)≠0が成り立たないY=F(X)+U", B ="外生性E(U|X)=0が成り立つY=F(X)+U") ) +
xlab("説明変数X") +
ylab ("目的変数Y") +
ggtitle("同じモデルF(X)=2+3Xであっても、外生性がある青と、外生性がない赤で、全く異なる。")+
theme_grey(base_family = "HiraKakuPro-W3")
#(参考)回帰分析
reg1 <- lm(Y ~ X + pattern + pattern*X)
summary(reg1)