ニ期間モデルは、時間を通じた合理的行動の基礎となる。二期間モデルは、異時点間の消費選択問題の最もシンプルな形式である。二期間モデルを言葉で説明すると、次のようになる。消費者は1期と2期の消費C、1期の貯蓄Sを選ぶことで、効用を最大化する。まず、1期の消費者は、所得Yを消費Cと貯蓄Sに分けて、消費によって効用を感じる。2期の消費者は、2期の所得Yと利子率rがプラスされた貯蓄(1+r)Sを、消費に回して効用を感じる。これを数式で表すと、次のようになる。
$$\max_{C_1,C_2,S} U(C_1,C_2)$$
$$s.t. C_1+S=Y_1$$
$$C_2=Y_2+(1+r)S$$
$$t期の消費C_t、t期の所得Y_t、貯蓄S、利子率r$$
二期間モデルの数式的な議論は付録に回すとして、本文では無差別曲線で議論してみよう。所与の所得(Y1, Y2)は予算制約線が必ず通る点となる。所得の点を通るように利子率に応じて予算制約線が引かれる。予算制約の中で最も効用が高くなるのは、予算制約線と無差別曲線が接する点である。1期の所得と1期の消費の差が、貯蓄である。マイナスの貯蓄ならば、それは借金を意味する。
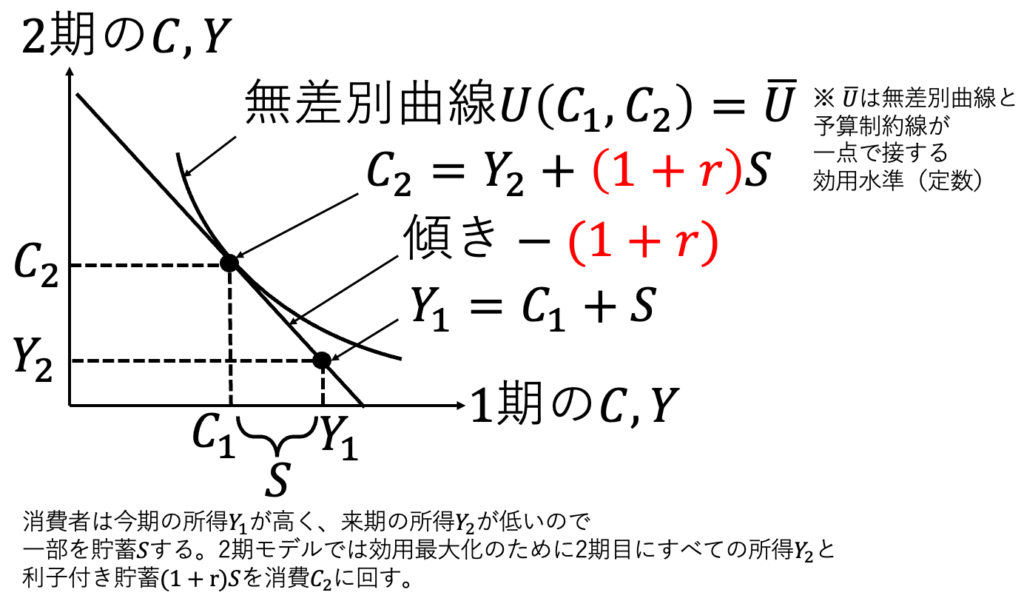
利子率は、将来得られる資本所得を失うために、今消費することで発生する機会費用であると解釈できる。上の最終的な結果を限界代替率=価格比と解釈し、来期にお金を使う価格P2を1とするならば、現在お金を使う価格はP1=1+rであり、利子率の分だけ余計に高い。なぜなら、お金は今期貯蓄すれば、来期に投資額×利子率が儲かるからだ。なお、違う解釈もできる。今期にお金を使う価格P1を1とするならば、来期にお金を使う価格はP2=1/(1+r)であり、現在価値にすると利子率の分だけ割り引かれていると言える。この二つの解釈の差は「今期が高い」「来期が安い」の差であり、同じことを述べている。
$$限界代替率MRS_{C_1,C_2}=\frac{MU_{C_1}}{MU_{C_2}}=\frac{1+r}{1}=価格比\frac{P_1}{P_2}$$
$$限界代替率MRS_{C_1,C_2}=\frac{MU_{C_1}}{MU_{C_2}}=\frac{1}{\frac{1}{1+r}}=価格比\frac{P_1}{P_2}$$
本文は以上。以下、付録。
執筆の目的
二期間モデルは、複数期間における意思決定を理解するのに役立つので、執筆した。
また、二期間モデルは「現在に使うお金は、我慢して来期に使うお金より、投資の平均的な利回り分をお高くつく」という資産形成を促す示唆をもたらすので、面白い。
問1:ラグランジュの未定乗数法で解く
本文では無差別曲線を用いて説明したが、数式でもちゃんと解いてみよう。
問1:次の二期間モデルを解いて、限界代替率=価格比の式を導け。これはオイラー方程式と呼ばれる。
$$\max_{C_1,C_2} U(C_1,C_2)$$
$$s.t. C_1+S=Y_1$$
$$C_2=Y_2+(1+r)S$$
$$t期の消費C_t、t期の所得Y_t、貯蓄S、利子率r$$
異時点間の消費選択問題は、ラグランジュの未定乗数法を用いて計算することができる。具体的には、次の通りである。制約条件は
$$Y_1-C_1-S=0、Y_2+(1+r)S-C_2=0$$
の二つである。そこでラグランジュ乗数λ1、λ2を用いて、ラグランジュ関数Lを次のように設定する。
$$L(C_1, C_2, S,\lambda_1,\lambda_2) $$
$$=U(C_1,C_2) + \lambda_1(Y_1-C_1-S)+ \lambda_2(Y_2+(1+r)S-C_2) $$
効用最大化の解において、C1, C2, Sについての偏微分がゼロなので
$$\frac{\partial L}{\partial C_1}=\frac{\partial U(C_1, C_2)}{\partial C_1}- \lambda_1=0…式(1)$$
$$\frac{\partial L}{\partial C_2}=\frac{\partial U(C_1, C_2)}{\partial C_2}- \lambda_2=0…式(2)$$
$$\frac{\partial L}{\partial S}=- \lambda_1+(1+r)\lambda_2=0…式(3)$$
式(1)式(2)を式(3)に代入すると
$$-\frac{\partial U(C_1, C_2)}{\partial C_1} +(1+r)\frac{\partial U(C_1, C_2)}{\partial C_2}=0$$
異時点間の消費選択を効用関数、利子率によって定式化したオイラー方程式は
$$\frac{\partial U(C_1, C_2)}{\partial C_1} =(1+r)\frac{\partial U(C_1, C_2)}{\partial C_2}$$
である。なお、発展的なモデルのオイラー方程式には、割引因子βやインフレ率πが導入される場合がある。ここで限界代替率=相対価格として、オイラー方程式を解釈してみよう。まずはわかりやすいように限界効用(MU, marginal utility)で表現する。
$$t期の消費C_tの限界効用をMU_{C_t}と表現すると$$
$$-MU_{C_1}+(1+r)MU_{C_2}=0$$
$$\frac{MU_{C_1}}{MU_{C_2}}=1+r$$
限界代替率(MRS, marginal rate of substitution)は限界効用の比であるので
$$異時点間消費の限界代替率MRS_{C_1,C_2}=1+利子率r$$
問2:金融市場の社会的意義
金融について「自分は何も生産しないくせに、金貸すだけで儲けている。ズルい」という批判がある。それは本当だろうか。
問2:金融市場の存在は社会厚生を改善するか。
消費者が貯蓄する人か、借金する人かで場合わけして考えよう。
(1)貯蓄者
問2(1):金融市場の存在は社会厚生を改善するか。貯蓄者(Saver)について考えよ。
貯蓄する人は、金融市場がある場合、次のような最適消費を選ぶ。

ここで、貯蓄する人が、金融市場を通じて誰かに貸すことができない場合、利子率がゼロという状況が生まれる。なぜなら、貯蓄したいならば、家の金庫でお金を保管し、ただし利息を受け取ることはできないからである。その結果、青の予算制約線から赤の予算制約線へ変化し、効用が小さくなる。

よって、貯蓄者については金融市場が存在することで、社会厚生が改善されるのである。
(2)借金者
問2(2):金融市場の存在は社会厚生を改善するか。借金者(Spender)について考えよ。
借金する人は、金融市場がある場合、次のような最適消費を選ぶ。
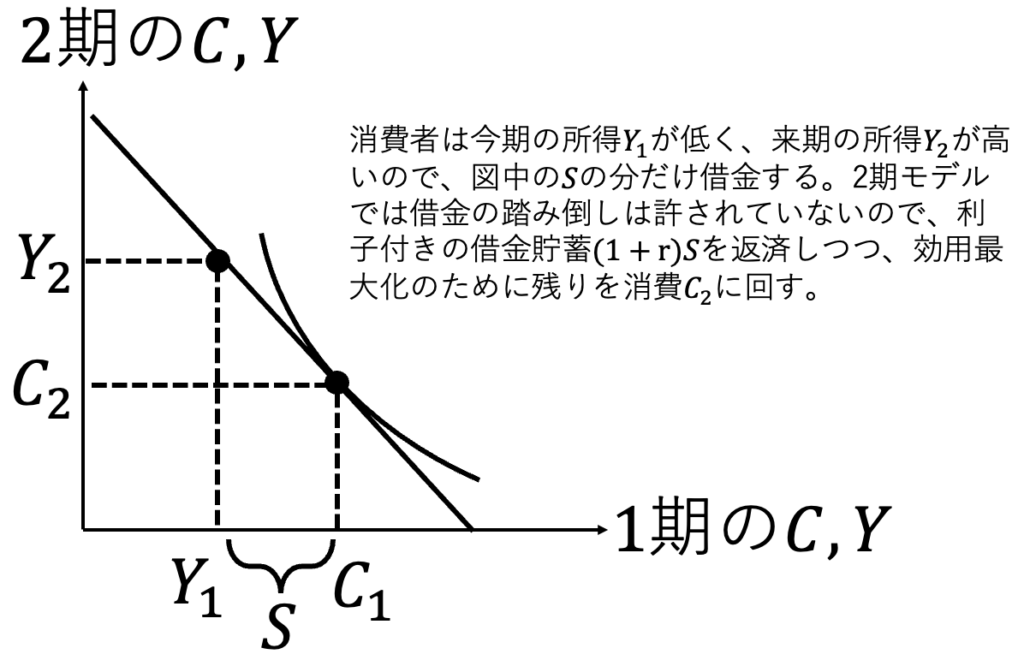
ここで、借金する人が、金融市場を通じて誰かから借りることができない場合、今期の所得以上の消費ができない状況が生まれる。経済学では借入制約と呼ばれる状況である。その結果、青の予算制約線から赤の予算制約線へ変化し、効用が小さくなる。

よって、貯蓄者については金融市場が存在することで、社会厚生が改善されるのである。
(3)まとめ
問2(3):以上の結果をまとめると、金融市場の存在は社会厚生を改善するか。
場合わけの結果をまとめると、金融市場があることで社会厚生は改善する。なぜなら、
・貯蓄者は誰かに貸し付けて、利息を得ることで消費を増やせ、効用を増大する。
・借金者は誰かから借り入れて、一時的に所得以上の消費を可能にし、効用を増大する。
というように、誰も損せずに、得する人がいるからである。つまり、パレート改善が起こっている。
問3:ゼロ金利制約
金利はゼロ金利制約によってマイナスにはならないと言われ、実際に銀行預金の金利は限りなくゼロに近いプラスでへばりついている。なぜだろうか。
問3:ゼロ金利制約を無差別曲線で説明せよ。
貸し手と借り手で分けて考えてみよう。
(1)貯蓄者
問3(1):ゼロ金利制約を無差別曲線で説明せよ。(貯蓄者の場合)
貯蓄者は、マイナス金利であるのならば、家の金庫で保管すればゼロ金利となり、セルフ利上げ政策を実施できる。つまり、貯蓄者は、マイナスの利回りの資産を基本的に買わない。ケインズ経済学的な言い方をすれば「ゼロ金利にて、流動性選好(=現金保有選好)が無限大になる。」
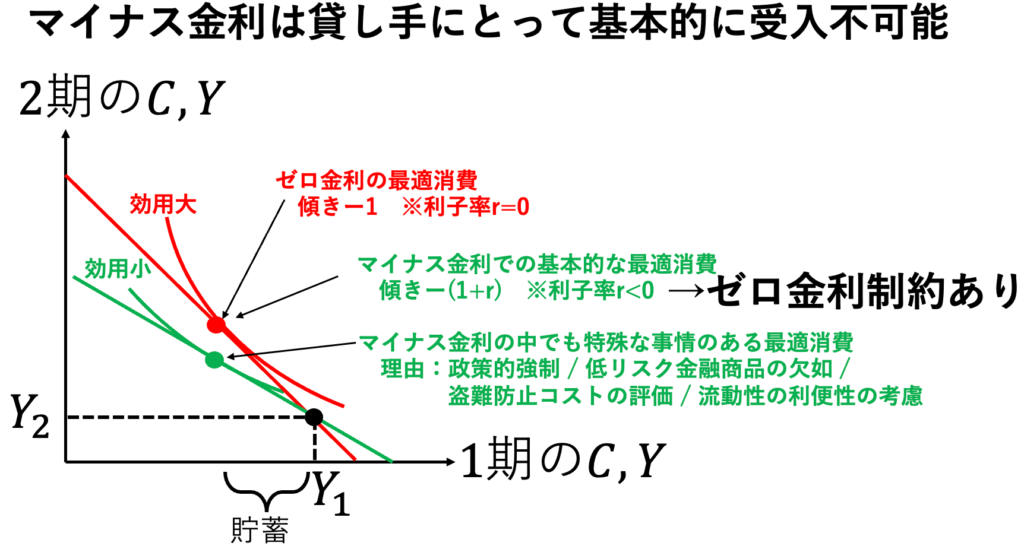
「貯蓄者は、マイナスの利回りの資産を『基本的に』買わない」といったのは、次のような基本的ではない状況ではマイナス金利を受け入れることを含意する。
・政策的な強制(税金みたいな…)
・低リスク商品の欠如(例えば、国債。ポートフォリオに加えるべき低リスクな資産がない場合は、マイナス金利の国債を買わざるを得ない。)
・盗難防止コストの評価(少額ならば家の金庫で保管するのでいいが、企業や資産家のように高額な資産の管理が必要な場合、マイナス金利を「保管料」と考えて払う可能性がある。)
・流動性の利便性考慮(銀行間の取引は電子データの受送信で完結するが、硬貨や紙幣といった現金では物理的な輸送が伴う。この現金の不便さゆえに、マイナス金利を手数料と考えて企業が受け入れる可能性はある。)
(2)借金者
問3(2):ゼロ金利制約を無差別曲線で説明せよ。(借金者の場合)
次に、借金者の場合を考えてみよう。マイナス金利とは、100万円借りたのに、返すのは99万円でいいというような状況である。当然、借金者としては歓迎すべき事態であるので、借金者はマイナス金利を喜んで受け入れる。

つまり、国としては国債を発行するなら、マイナス金利、低金利政策、金融緩和の持続が望ましいわけだ。
(3)まとめ
問3(3):以上の結果をまとめると、ゼロ金利制約の発生メカニズムを述べよ。
場合わけの結果をまとめると、基本的に金利はマイナスにならない。なぜなら、マイナス金利を受け入れる貸し手が存在しないからだ。ただし、貯蓄者に次のような例外的な場合が発生すると、喜んでマイナス金利を受け入れる借金者との間で、マイナス金利が実現する可能性がある。
・政策的な強制
・低リスク商品の欠如
・盗難防止コストの評価
・流動性の利便性考慮
