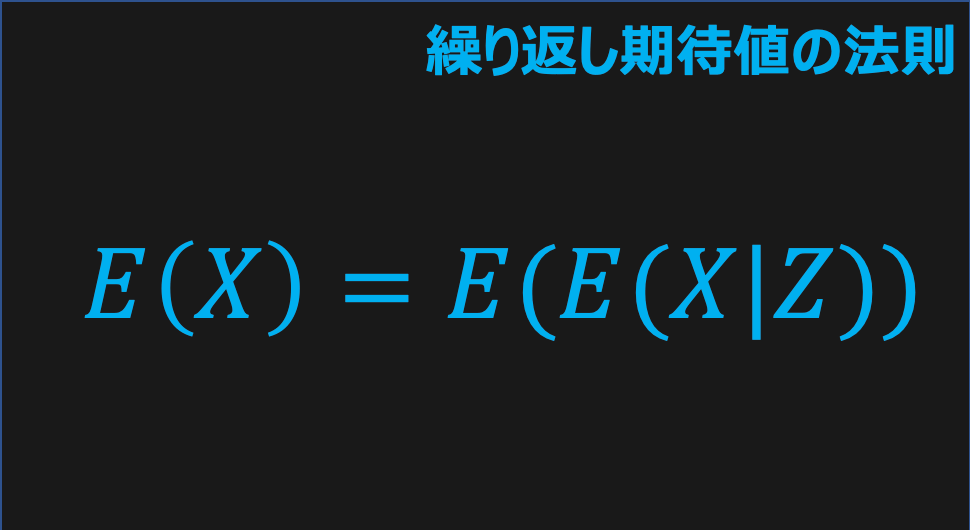繰り返し期待値の法則とは、「条件付き期待値E(Y|X)の期待値」は「確率変数Yの期待値」と等しいという法則である。英語ではthe law of total expectation、the law of iterated expectations(LIE)と呼ばれる。数式では、以下の通りだ。
$$繰り返し期待値の法則:E(E(Y|X))=E(Y)$$
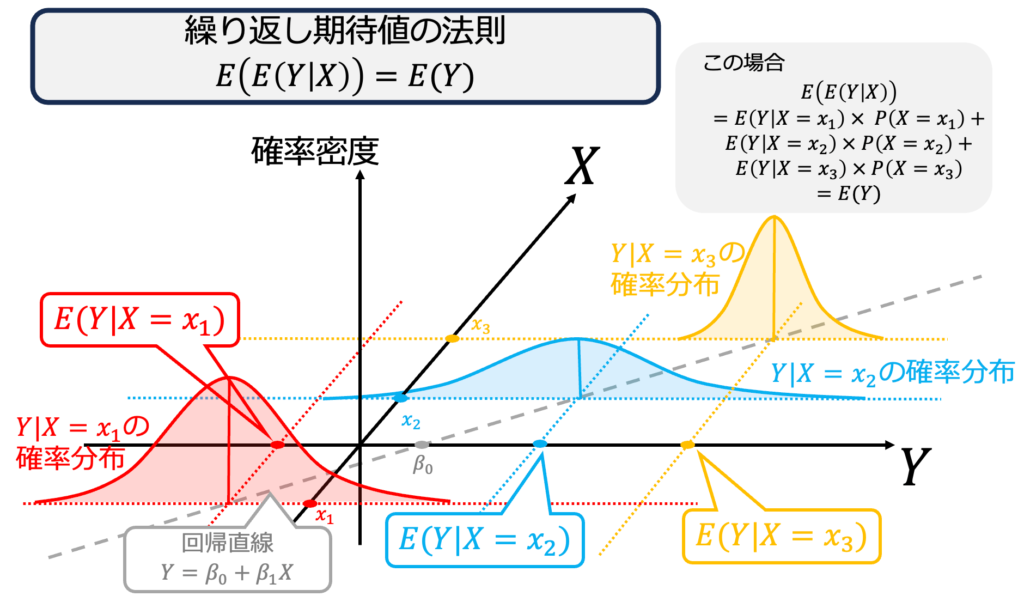
補足:回帰モデルと解釈するならば、上は「誤差項が不均一分散」している回帰モデルと言える。
離散型確率変数についての繰り返し期待値の法則を証明する。なお、この数式の詳細は付録の問1〜3でわかりやすく説明した。
$$E(E(Y|X))=\sum_{j=1}^m \Big( E(Y|x_j) \Big) P(x_j) \cdots 期待値の定義より$$
$$=\sum_{j=1}^m \left( \sum_{i=1}^n y_i P(y_i|x_j) \right) P(x_j) \cdots 条件付き期待値の定義より$$
$$=\sum_{i=1}^n \sum_{j=1}^m y_i P(y_i|x_j) P(x_j) \cdots \sum_{i=1}^n と \sum_{j=1}^m は入替可より$$
$$=\sum_{i=1}^n y_i \sum_{j=1}^m P(y_i|x_j) P(x_j) \cdots \sum_{j=1}^mの内部においてiは定数扱い$$
$$=\sum_{i=1}^n y_i P(y_i) \cdots 付録問2(2)より$$
$$=E(Y) \cdots 期待値の定義より$$
繰り返し期待値の法則は、回帰分析の証明において威力を発揮するので知っておくとよい。なぜなら、条件付き期待値で表せるモデルである回帰モデルにおいて、条件付き期待値を処理するたびに繰り返し期待値の法則の出番がやってきうるからである。
$$重回帰モデル:Y=\beta_0 +\beta_1 X_1+\beta_2 X_2 +\cdots \beta_k X_k+U$$
$$重回帰モデル:E(Y|X_1,X_2 \cdots X_k)=\beta_0 +\beta_1 X_1+\beta_2 X_2 +\cdots \beta_k X_k$$
本文は以上。以下、付録。
執筆の目的
繰り返し期待値の法則は、回帰モデルにおける推定量の性質を導く際にとても役に立つので、執筆した。
また、繰り返し期待値の法則からは「状況Xが不明ならば、現状Yは平均的な現象E(Y)と考えるべし」という示唆が得られるので、面白い。
問1:期待値
繰り返し期待値の法則の前に、そもそも「条件付き期待値」とは一体何だろうか。
(0)前提
まず表記法についての前提が共有しよう。
前提:次の表記法①〜④を前提とする。
・前提①:確率変数は、大文字で表す。この記事では離散型確率変数を想定する。
・前提②:定数は小文字で表す。
・前提③:確率P(y)を、確率変数Yが定数yを取る確率とする。
・前提④:条件付き確率P(y|x)を、確率変数Xが定数xを取るという条件で、確率変数Yが定数yを取る確率とする。
(1)期待値E(Y)
そもそも期待値E(Y)の定義はなんだろうか。
問1(1):離散型確率変数Yの期待値E(Y)とは何か。
離散型確率変数Xの期待値E(Y)は
$$E(Y)=\sum_{i=1}^n y_i P(y_i)$$
※Yはn種類の値を取りうるとする。
と定義できる。
わかりやすく解説しよう。期待値とは「確率変数Yが平均的にどの値になるか」についての概念である。「取りうる値」に「それを取る確率」をかけて合計する。これは加重平均と呼ばれる数学的操作である。具体的には
$$番号i=1のとき、y_1 P(y_1)$$
$$番号i=2のとき、y_2 P(y_2)$$
$$\cdots$$
$$番号i=nのとき、y_n P(y_n)$$
をすべて足す(Σ)。
(2)条件付き期待値E(Y|x)
E(Y|X)の前に、条件付き期待値E(Y|x)について考えてみよう。
問1(2)条件付き期待値E(Y|x)とは何か。
確率変数Xが定数xを取る際の、条件付き期待値E(Y|x)とは、何だろうか。
$$E(Y|x)=\sum_{i=1}^n y_i P(y_i|x)$$
条件付き期待値E(Y|x)は
$$E(Y|x)=\sum_{i=1}^n y_i P(y_i|x)$$
と定義する。これも考え方は先ほどと同じである。
$$番号i=1のとき、y_1 P(y_1|x)$$
$$番号i=2のとき、y_2 P(y_2|x)$$
$$\cdots$$
$$番号i=nのとき、y_n P(y_n|x)$$
をすべて足す(Σ)。
(3)E(Y|X)のランダム性
さて、繰り返し期待値の法則は「E(Y|X)の期待値がE(Y)」と主張するが、そもそもなぜE(Y|X)は確率変数なのか。
問1(3)E(Y|X)は確率変数であるか。
条件付き期待値E(Y|x)
$$E(Y|x)=\sum_{i=1}^n y_i P(y_i|x)$$
は確定変数である。
しかし、xが複数の値をランダムに取る場合、話は変わってくる。離散型確率変数Xが母集団分布にしたがって生み出される際の、条件付き期待値E(Y|X)
$$E(Y|X)=\sum_{i=1}^n y_i P(y_i|X)$$
は確率変数である。なぜなら、Xはm種類の値を取りうるとすると、条件付き期待値E(Y|X)は、
$$E(Y|x_1) \cdots P(x_1)の確率でありうる$$
$$E(Y|x_2) \cdots P(x_2)の確率でありうる$$
$$\cdots$$
$$E(Y|x_m) \cdots P(x_m)の確率でありうる$$
と言える。したがって、条件付き期待値E(Y|X)は、最大でm種の値を取りうる確率変数になっている。
(4)E(Y|X)=0
少し脱線するが、重回帰モデルでは外生性E(U|X)=0の仮定が課される。Uは誤差項、Xは説明変数である。E(U|X)=0は一体何を意味するのだろうか。
問1(4)E(Y|X)=0とは何か。Xはm種類の値を取りうるとする。
問1(3)よりE(Y|X)は確率変数である。にも関わらず、定数の0を取るということは、次のことを意味する。
$$E(Y|x_1)=0 \cdots P(x_1)の確率でありうる$$
$$E(Y|x_2)=0 \cdots P(x_2)の確率でありうる$$
$$\cdots$$
$$E(Y|x_m)=0 \cdots P(x_m)の確率でありうる$$
つまり、Xがどんな値であっても、Yの条件付き期待値が0のとき、
$$E(Y|X)=0$$
と表せる。外生性E(U|X)=0とは「どんなXであっても、誤差項Uの条件付き期待値は0である」ことを意味する。
問2:条件付き確率
本文中にて
$$P(y)=\sum_{j=1}^m P(y|x_j) P(x_j)$$
という計算をしている。これについて説明する。
(1)積事象の確率
繰り返し期待値の法則には、XとYの二つの変数があり、二つの事象が同時に起こっている。ならば、二つの事象が同時に起こる確率について理解を深めないといけない。
問2(1)二つの事象が同時に起こる確率はどう表現できるか。
「確率変数X=定数x」かつ「確率変数Y=定数y」になる積事象の確率は
$$P(X=xかつY=y)=P(y|x) P(x)$$
で表せる。なぜなら、まず確率変数X=xになり、その上でY=yとなる確率は
$$P(x) \times P(y|x) $$
であり、これはX=xかつY=yとなる確率だからである。
(2)P(y)=ΣP(y|x)P(x)
本文ではP(y)=ΣP(y|x)P(x)という計算がなされているが、これを理解したい。
問2(2)本文のP(y)=ΣP(y|x)P(x)という計算はなぜ成立するのか。
本文で登場した
$$P(y)=\sum_{j=1}^m P(y|x_j) P(x_j)$$
を直感的に示す。まず、積事象の確率より、上式は
$$\sum_{j=1}^m P(y|x_j) P(x_j)=\sum_{j=1}^m P(yかつ x_j) \cdots 積事象の確率$$
となる。
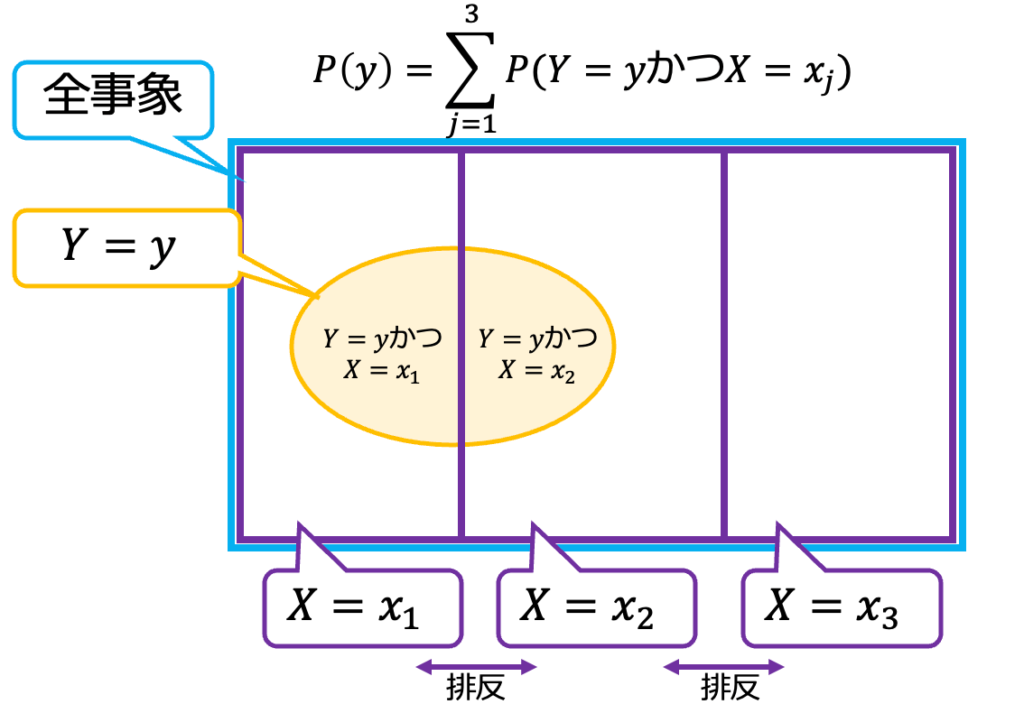
次に、確率変数Xは同時に同じ値を取ることはできず、排反であることに注目する。Σでj=1,2・・・mを考えるとは、すべての場合をモレなくダブりなく考えることを意味する。ということは、これらを合計すると
$$\sum_{j=1}^m P(yかつ x_j)=P(y)$$
となる。
要は「Yをすべての場合に分けてから、すべての場合について足し合わせたら、もともとのYができました!」という当たり前の話である。これをわかりやすく図解しよう。m=3の場合は、次のように表せる。
問3:繰り返し期待値の法則の証明
本文の再掲になるが、繰り返し期待値の法則の証明をする。期待値の定義、E(Y|X)が確率変数であることと、P(y)=ΣP(y|x)P(x)について理解した今ならば、より深く理解できると思う。
問3:繰り返し期待値の法則は正しいのか。
離散型確率変数についての繰り返し期待値の法則を証明しよう。
$$E(E(Y|X))=\sum_{j=1}^m \Big( E(Y|x_j) \Big) P(x_j) \cdots 期待値の定義より$$
$$=\sum_{j=1}^m \left( \sum_{i=1}^n y_i P(y_i|x_j) \right) P(x_j) \cdots 条件付き期待値の定義より$$
$$=\sum_{i=1}^n \sum_{j=1}^m y_i P(y_i|x_j) P(x_j) \cdots \sum_{i=1}^n と \sum_{j=1}^m は入替可より$$
$$=\sum_{i=1}^n y_i \sum_{j=1}^m P(y_i|x_j) P(x_j) \cdots \sum_{j=1}^mの内部においてiは定数扱い$$
$$=\sum_{i=1}^n y_i P(y_i) \cdots 本記事問2(2)より$$
$$=E(Y) \cdots 期待値の定義より$$
したがって、繰り返し期待値の法則
$$E(E(Y|X))=E(Y) $$
が離散型変数について示された。