「Xが1増えるとYが何%増えるのか」を知りたいならば、ログ=レベル・モデルという重回帰モデルを使う。β×100が求めたい「何%」の近似値となっているし、正確な%も計算可能だ。logYは事前に計算してあげて、あとは最小二乗法で重回帰分析してやれば、βが推定できる。
$$モデル \log_e Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k+U$$
$$X_1が1増えるとYは約(100 \times \beta_1) \% 増える$$
$$正確には、100 \times (e^{\beta_1}-1) \%増える$$
なぜYは(100×β)%増えるのか? それは正確にはYは(e^β-1)の割合で増え、βが0近傍では(e^β-1)≒βだからだ。
$$\log_e Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k+Uより$$
$$Y=e^{(\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k+U)}である。ここで$$
$$Y=f(X_1)=e^{\beta_1 X_1 +他}として$$
$$Y+\Delta Y=f(X_1+1)=e^{\beta_1 (X_1+1) +他}と定義すると$$
$$増加率=\frac{\Delta Y}{Y}$$
$$=\frac{Y+\Delta Y-Y}{Y}$$
$$=\frac{f(X_1+1)-f(X_1)}{f(X_1)}$$
$$=\frac{f(X_1+1)}{f(X_1)}-1$$
$$=\frac{e^{\beta_1 (X_1+1) +他}}{e^{\beta_1 X_1 +他}}-1$$
$$=e^{\beta_1}-1となる。ところで図1より$$
$$増加率=e^{\beta_1}-1≒\beta_1$$
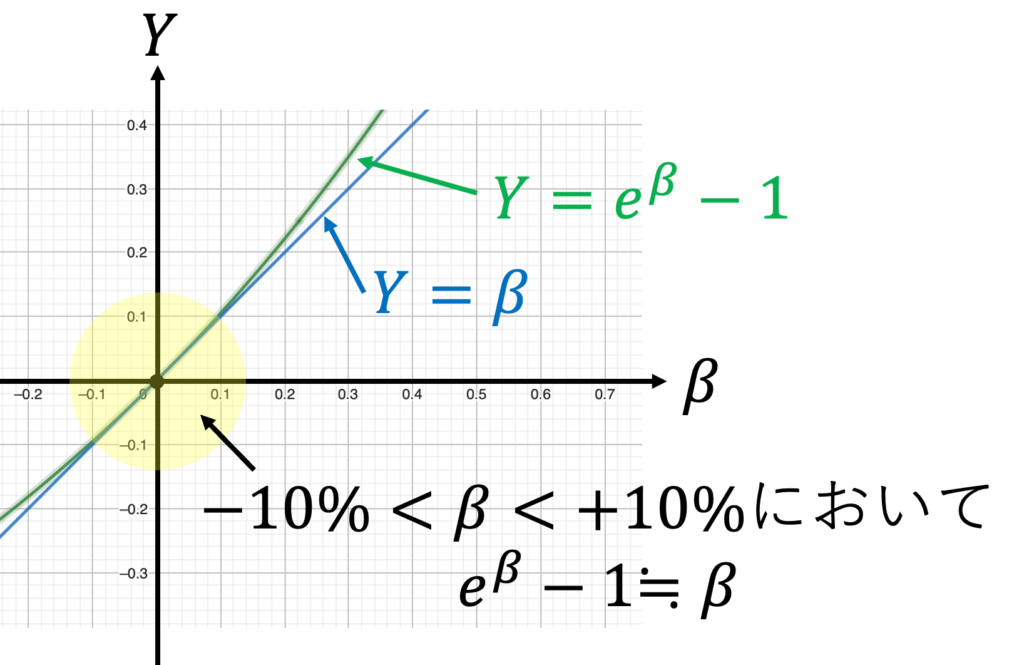
変数の側を処理して線形回帰モデルに帰着できるのならば、このような非線形なモデルでも線形回帰分析ができる。例えば「教育年数が1年増えると、賃金は何%上がるのか」というミンサー型賃金関数は、このようなログ=レベル・モデルの重回帰モデルで表現されている。
【追記】
ミンサー型賃金関数は、次の式で表現される賃金関数である。このとき、β1は教育の収益率になる。川口大司(2011)「ミンサー型賃金関数の日本の労働市場への適用」,経済産業研究所.の15ページにて、川口はβ1=0.10と推定している。
$$\log(賃金)=\beta_0+\beta_1(教育年数)+\beta_2(社会人歴)+\beta_2(社会人歴)^2+U$$
