「考え方が正しいなら、過去の現象を説明できる確率が高いはずだ」と考えるのは当然だ。ただし、最尤法は、少々極端で「最も起こりやすい現象が発生した」と考えてパラメーターを推定する。
最尤法(maximum likelihood estimation, MLE)は、標本が実現する確率が最大になるようなパラメーターを推定値とする方法である。パラメーターの推定値を入力すると、標本が実現する確率が出力される関数を、尤度関数と呼ぶ。最尤法は、この尤度関数を最大化する推定値を計算する。具体的には、次の通りである。
$$Xという条件でYになる確率P(Y|X)が$$
$$f_Y(X, \beta)であるという統計モデルを考える。$$
$$Xは説明変数、Yは目的変数、\betaはパラメーターである。$$
$$(x_1,y_1),(x_2,y_2) \cdots (x_n,y_n)という標本が得られた。$$
$$nはサンプル・サイズである。$$
$$この標本が得られる確率は$$
$$P(y_1|x_1)P(y_2|x_2) \cdots P(y_n|x_n)$$
$$=f_{y_1}(x_1, \beta)f_{y_2}(x_2, \beta) \cdots f_{y_n}(x_n, \beta)$$
$$である。この確率をLとする。$$
$$データ分析者にとって\betaは未知である。$$
$$パラメーター\betaの推定値\widehat{\beta}を求めたい。$$
$$標本は、最も起こりやすい現象が起きた結果と考える。$$
$$標本が得られる確率Lを\widehat{\beta}の尤度関数L(\widehat{\beta})と見立てて$$
$$L(\widehat{\beta})を最大化する\widehat{\beta}を計算する。$$
$$これが最尤法による推定である。$$
現実世界において、ありえた別の人生の可能性を夢想することは、むなしい。たしかに、確率論で考えれば、どんな可能性もありえた。しかし、それを言ってもキリがない。ならば、過去に起きたことはすべて起こりうる現象の中で最も確率が高かったと思った方が踏ん切りが付く。最尤法には、そんなような思い切りのいい諦念が込められている気がする。
【追 記】
尤度関数はそのままだととても扱いにくい。そこで、対数をとった対数尤度関数を最大化する方法がよく取られる。計算がしやすいからだ。
$$尤度関数L=f_{y_1}(x_1, \beta) \times \cdots \times f_{y_n}(x_n, \beta)$$
$$対数尤度関数\log L=\log f_{y_1}(x_1, \beta)+ \cdots + \log f_{y_n}(x_n, \beta)$$
対数化しても全く問題ない。尤度関数を最大にするパラメーターと、対数尤度関数を最大にするパラメーターは一致するからだ。なぜなら、図1の通りに対数は単調増加するからである。
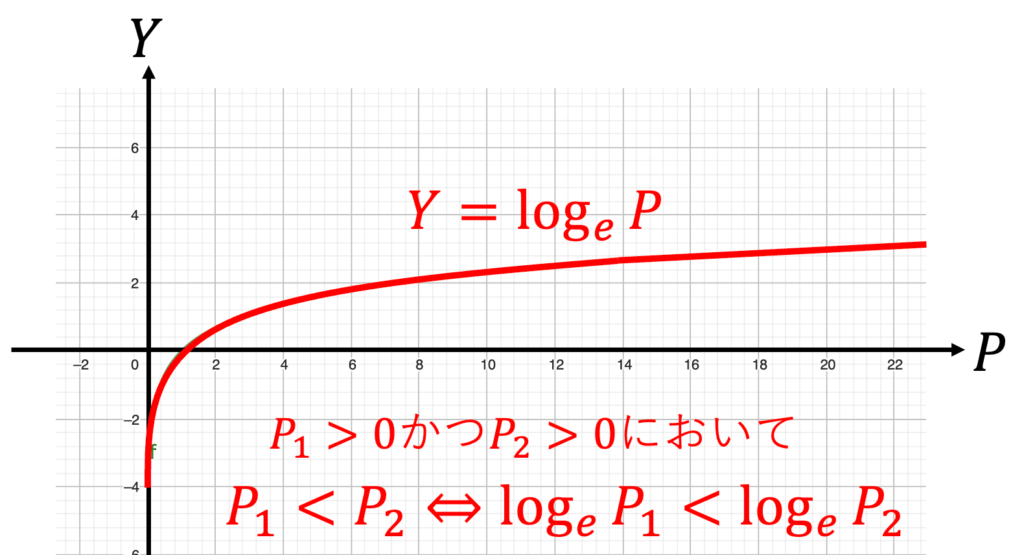
出典:しまうま総研(2023)
補足:作図にはGeoGebraを用いた。
