最小二乗推定量の不偏性・一致性・漸近正規性について / 重回帰分析

　重回帰モデルには画像１のように最大で7個の仮定が課される。仮定１〜４が成り立てば、最小二乗推定量は不偏性、一致性、漸近正規性を持つ。仮定１〜６が成り立てば、ガウス・マルコフの定理より、最小二乗推定量が最良線形不偏推定量（Best Linear Unbiased Estimator, BLUE）になる。定５〜７は緩和できる仮定である。「仮定７：正規性」の違反はサンプル・サイズを増やすことで、「仮定６：均一分散」の違反は不均一分散に頑健な標準誤差（HC標準誤差、ロバスト標準誤差）を用いることで、「仮定５：自己相関しない」の違反は不均一分散と自己相関に対して一致性を持つ標準誤差（HAC標準誤差、クラスター・ロバスト標準誤差）を用いることで対処可能である。

　

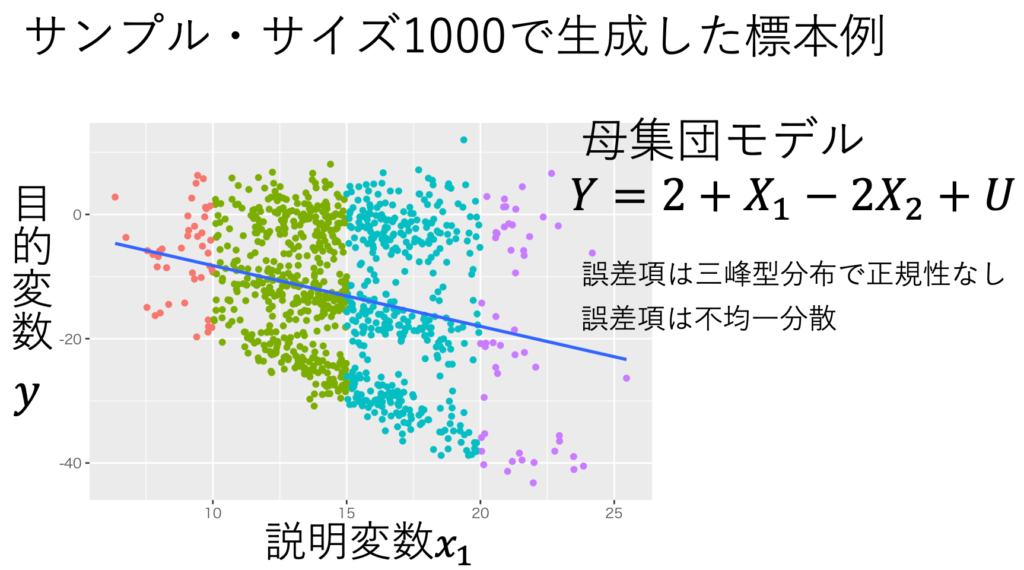
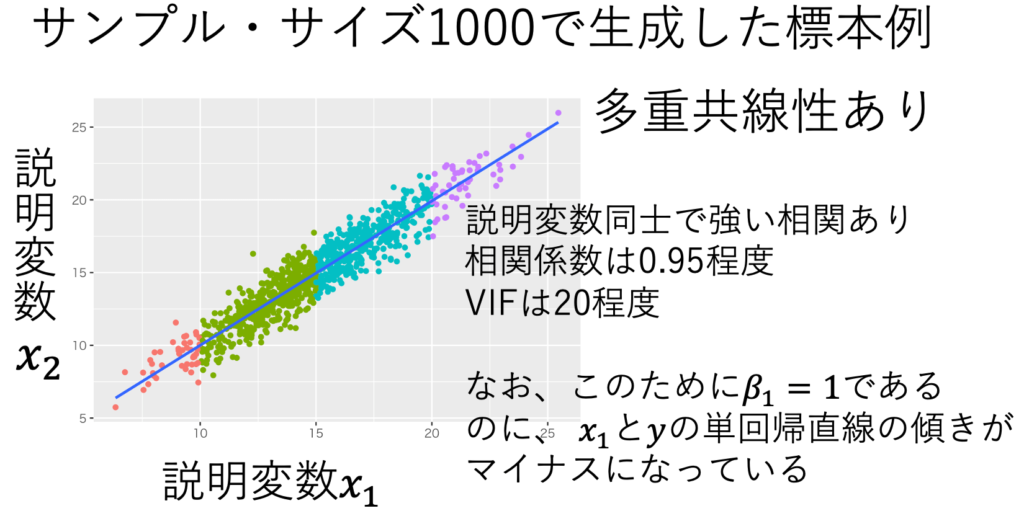
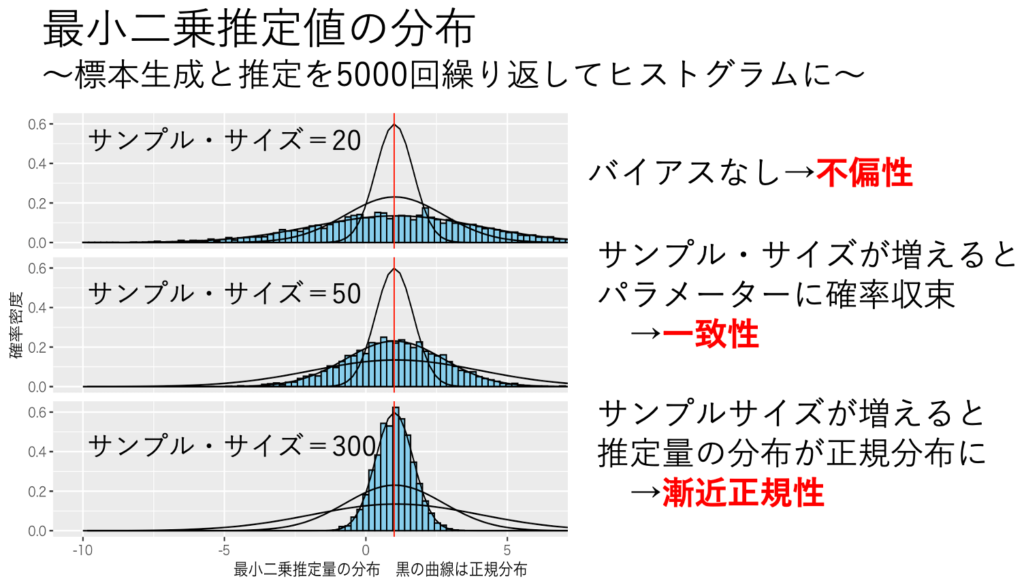
　「仮定１〜４が成り立てば、最小二乗推定量は不偏性、一致性、漸近正規性を持つ」をシミュレーションで検証する。このシミュレーションではあえて「多重共線性、誤差項の不均一分散、誤差項の非正規性」な状況を作り出し、これらの違反があっても不偏性、一致性、漸近正規性が保たれることを示す。具体的には、図１のような重回帰モデルに従う標本を乱数生成し、重回帰分析をする。図1からは誤差項の不均一分散、誤差項の非正規性が見て取れる。図２からは多重共線性が見て取れる。これを5000回繰り返して、最小二乗推定値の分布を調べる。その結果、図3より、最小二乗推定量が不偏性、一致性、漸近正規性をもつことが確認できた。

　

　

　

　重回帰分析を使う上での障壁が「①定式化の誤り」「②無作為抽出」「④外生性」に絞り込まれた。③はダミー変数以外で問題になることは、ほぼないだろう。また、冒頭に述べた通り、「⑤誤差項が自己相関していない」「⑥誤差項が均一分散している」「⑦誤差項は正規分布に従う」 「⑧多重共線性がある」は問題にならない。

　　

【追記】

　このシミュレーションでは、次のように考えてモデルを組んだ。

①重回帰モデルという定式化に誤りがない　→　説明変数と誤差項を乱数発生させて、目的変数を計算した

②無作為抽出　→　乱数発生が無作為抽出と同じ役割を果たす。一つ一つの標本は、独立同一の母集団分布に従う。

③完全な共線関係が存在しない　→　説明変数同士の相関係数が+1か-1にならなければ良い

④外生性　→　説明変数と誤差項が無相関になるように生成した。

⑤誤差項が自己相関していない　→　誤差項は一つ一つ生成した。（本来なら自己相関もさせたかったが、自己相関させつつ不均一分散で非正規性をもち、外生性を満たす誤差項を作るのは、少々難しかった。）

⑥誤差項の均一分散についての違反　→　Xと無相関で期待値0の誤差項に、Xをかけてやることで、Xが大きなのなると分散が大きくなる誤差項を作った。

⑦誤差項の正規性についての違反　→　三峰型分布になる乱数を1万個生成し、その平均が0になるように調整した誤差項の候補をプールしておいた。必要に応じて、そのプールからランダムに取り出して、誤差項とした。

⑧多重共線性　→　X2 = X1 + e という形で、X1を生成した後、分散の小さな正規分布に従うeを足してやることで、X2を作った。

　シミュレーションと描画のためのRコードは次の通り。パッケージはggplot2とtidyverseを用いた。

#パッケージの呼び出し
library(ggplot2)
　
#正規分布していない誤差項を作る
u_size <- 10000　
u0 <- rep(NA, u_size)
u1 <- rep(NA, u_size)
for(i in 1:u_size){
  u0[i] <- ifelse(i < 3000,rnorm(1,-10,1) , 
                  ifelse(i < 6000, rnorm(1,-2,1),rnorm(1,7,2)))
}
for(i in 1:u_size){
  u1[i] <- 0.1*(u0[i] - mean(u0))　
}
data_u <- data.frame(u1) 
ggplot(data_u, aes( x = u1)) + 
  geom_histogram( bins=50,aes( y = ..density.. ),colour="white", fill = "pink2")+
  stat_function(fun = dnorm, args=list(mean=mean(data_u$u1), sd=sqrt(var(data_u$u1))))+
  xlab("誤差項U") + 
  ylab ("確率分布") +
  ggtitle ("誤差項Uの確率分布　　黒はUと同じ期待値、分散の正規分布") +
  theme_grey(base_family = "HiraKakuPro-W3")
　
#説明変数と不均一分散する誤差項を作る
sample_size0 <- 1000 #サンプル・サイズを500
x1<- rnorm(sample_size0, 15,3)
x2 <- x1+rnorm(sample_size0, mean =0, sd=1)
u_x <- rep(NA, sample_size0)
for(i in 1:sample_size0){ 
  uu <- sample(u1, 1, replace = TRUE)
  u_x[i] <- uu*x1[i]
}
cor(x1,x2)
　
#標本を作る
y <- 2 + 1*x1- 2*x2 +u_x
category <- 
  ifelse(x1　<=　10,"~10",
         ifelse(x1 <= 15 ,"10~15",
                ifelse(x1 <= 20, "15~20","20~")))
data0 <- data.frame(x1, x2, y, u_x,category)　
ggplot(data0, aes(x = x1,y=y)) +　
  geom_point(aes(colour=category) ) +
  stat_smooth(method = "lm", formula='y~x', se = FALSE)+
  xlab("説明変数X") + 
  ylab ("目的変数Y") +
  ggtitle ("サンプル・サイズ1000で標本を生成した例") +
  theme_grey(base_family = "HiraKakuPro-W3")
ggplot(data0, aes(x = x1,y=x2)) +　
  geom_point(aes(colour=category) ) +
  stat_smooth(method = "lm", formula='y~x', se = FALSE)+
  xlab("説明変数X") + 
  ylab ("目的変数Y") +
  ggtitle ("サンプル・サイズ1000で標本を生成した例") +
  theme_grey(base_family = "HiraKakuPro-W3")
　
#最小二乗推定量の分布を生成する
trial_number <- 5000　#試行回数
beta_1_size1 <- rep(NA, trial_number)　
beta_1_size2 <- rep(NA, trial_number)　
beta_1_size3 <- rep(NA, trial_number)
　
#n=20、1000回標本生成と回帰分析を繰り返す
sample_size1 <- 20
u_x <- rep(NA, sample_size1) 
for(j in 1:trial_number){ 
  x1 <- rnorm(sample_size1, 15,3)
  x2 <- x1+rnorm(sample_size1, mean =0, sd=1)
  for(i in 1:sample_size1){ 
    uu <- sample(u1, 1, replace = TRUE)
    u_x[i] <- uu*x1[i]
  }
  y <- 2 + 1*x1- 2*x2 +u_x
  answer <- lm(y~x1+x2)
  beta_1_size1[j] <- summary(answer)$coef["x1","Estimate"]
}
　
#n=50、1000回標本生成と回帰分析を繰り返す
sample_size2 <- 50
u_x <- rep(NA, sample_size2) 
for(j in 1:trial_number){ 
  x1 <- rnorm(sample_size2, 15,3)
  x2 <- x1+rnorm(sample_size2, mean =0, sd=1)
  for(i in 1:sample_size2){ 
    uu <- sample(u1, 1, replace = TRUE)
    u_x[i] <- uu*x1[i]
  }
  y <- 2 + 1*x1- 2*x2 +u_x
  answer <- lm(y~x1+x2)
  beta_1_size2[j] <- summary(answer)$coef["x1","Estimate"]
}
　
#n=300、1000回標本生成と回帰分析を繰り返す
sample_size3 <- 300
u_x <- rep(NA, sample_size3) 
for(j in 1:trial_number){ 
  x1 <- rnorm(sample_size3, 15,3)
  x2 <- x1+rnorm(sample_size3, mean =0, sd=1)
  for(i in 1:sample_size3){ 
    uu <- sample(u1, 1, replace = TRUE)
    u_x[i] <- uu*x1[i]
  }
  y <- 2 + 1*x1- 2*x2 +u_x
  answer <- lm(y~x1+x2)
  beta_1_size3[j] <- summary(answer)$coef["x1","Estimate"]
}
　
#推定量の分布の描画
library(tidyverse)
tibble(size020=beta_1_size1, size050=beta_1_size2, size300=beta_1_size3)%>% 
  gather(key=n,value=value,size020,size050,size300)%>% 
  ggplot() +
  geom_histogram(aes(x = value, y =..density..),bins=100,fill="skyblue", color= "black") +
  stat_function(fun = dnorm, args=list(mean=mean(beta_1_size1), sd=sqrt(var(beta_1_size1))))+
  stat_function(fun = dnorm, args=list(mean=mean(beta_1_size2), sd=sqrt(var(beta_1_size2))))+
  stat_function(fun = dnorm, args=list(mean=mean(beta_1_size3), sd=sqrt(var(beta_1_size3))))+
  geom_vline(xintercept = 1, color = "red") +
  facet_grid(n~.)+
  xlab("最小二乗推定量の分布　黒の曲線は正規分布") + 
  ylab ("確率密度") +
  theme_grey(base_family = "HiraKakuPro-W3")