ニューケインジアン・モデルでは、最適財政政策を論じることができる。なお、最適財政政策は「自由競争に全てを任せる」ではない。財政政策がなければパレート最適な経済状態が実現しない。必要とされる財政政策は、市場の失敗への対処である。具体的には、独占的競争をしている中間財企業は、生産量を制限し、中間財価格を釣り上げ、独占利潤を確保しようとする。その結果、死荷重が発生する。その結果が図1である。独占企業は限界収入曲線と限界費用曲線が交わるところで独占供給量を決定する。その次に、その独占供給量での逆需要関数で独占価格を定める。すると、図1のように独占価格と限界費用が一致せず、三角形に近似される領域で死荷重が発生する。
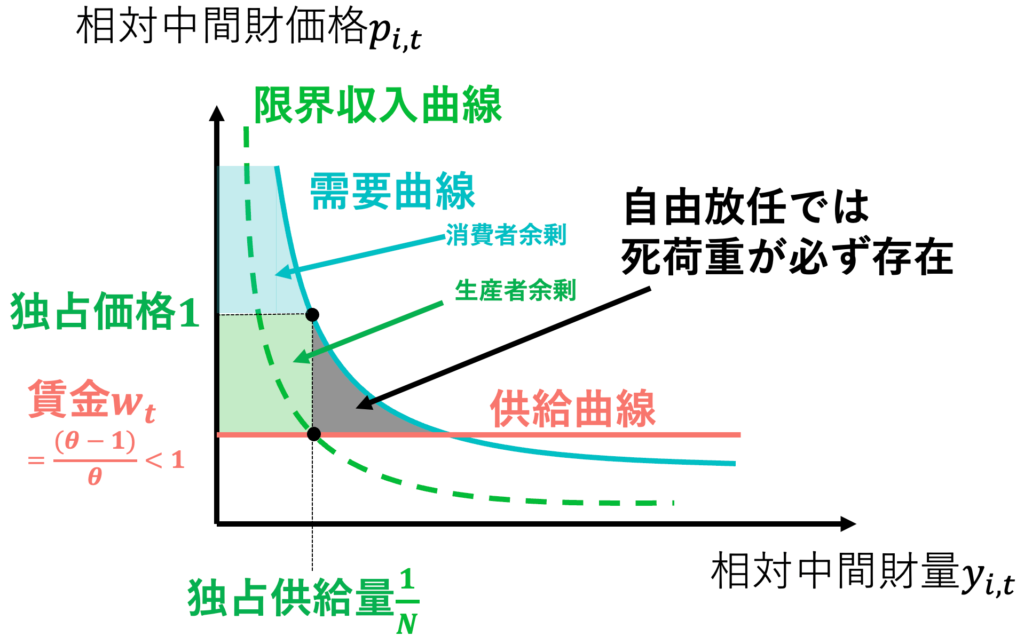
独占という市場の失敗に対して、パレート最適な資源分配を達成するための政策は、限界費用価格形成原理に基づき、独占価格を決定し、赤字額を政府が補償することである。補助金は中間財企業の生産に対して課せられるので、限界収入を増加させる。一方で、中間財企業への補助金は巡り巡って、家計にも行き渡り、賃金も増加させる。計算すると、死荷重が生まれない最適補助金率=1/(θ-1)になる。
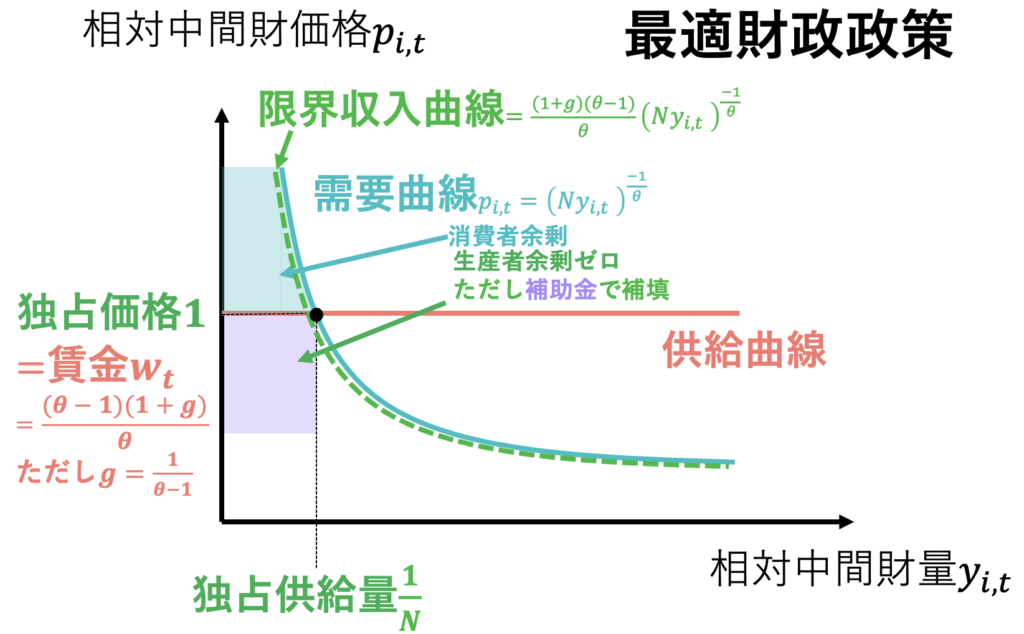
結論は「最適な財政政策は存在する=財政支出には最適な水準が存在する(図2)」「最適な財政政策とは市場の失敗に対処することである=独占によって生まれた死荷重をゼロにするための限界費用価格形成と補助金政策である(図2)」である。とてもミクロ経済学的な結論だ。もっと言えば「過小あるいは過大な財政政策は存在する」例えば「自由競争に任せると、独占企業によって死荷重が発生する(図1)」「過度な補助金政策を行うと、死荷重をうむ」と言える。
「ニューケインジアン・モデル」解説シリーズ
企画:「しまうま総研 より良い社会のための思考法 / 3段落で簡潔明瞭」>「よりよい社会のための経済学入門」>「ニューケインジアン・モデルについて」
第1回:ニューケインジアン・モデルについて(必読 / 難易度中)
第2回:家計、最終財企業、中間財企業、市場均衡条件のミクロ的基礎について (スキップ可 / 難易度高)
第3回:非線形動学と非線形定常均衡について(スキップ可 / 難易度高)
第4回:対数線形化と対数線形近似について(スキップ可 / 難易度高)
第5回:テイラー・ルールと定常均衡について
第6回:中間財市場と最適財政政策について(必読 / 難易度中)
第7回:労働市場と非効率な雇用水準について
第8回:最終財市場とGDPギャップについて
第9回:独占的競争と短期なインフレについて
第10回:粘着的な価格とインフレの平準化について
第11回:最適金融政策とインフレ・バイアスについて
第12回:動学的確率的一般均衡モデルへの拡張について
第13回:Dynareを用いたシミュレーションについて
補講:DynareをMATLABで動かすための環境構築について / DynareをOctaveで動かすための環境構築について
主要な参考資料
・仲田泰祐(2020)「ゼロ金利制約下の 金融政策 FRBの政策運営」 (モデルは仲田(2020)と同じ)
・楡井誠(2023)「マクロ経済動学: 景気循環の起源の解明」
結論
財政政策は、市場の失敗への対処のために必要である。自由な市場に任せると、中間財価格と中間財生産の限界費用に差が生まれ、死荷重を生む(問A)。
中間財価格と中間財生産の限界費用が等しくなり、死荷重を生まない最適な補助金率は
$$最適な補助金率g=\frac{1}{\theta -1}$$
である(問B)。
モデル:ニューケインジアン・モデル
・【モデル本体】ニューケインジアン・モデルについて / 景気循環
・【モデルの解】ニューケインジアン・モデルでの動学的一般均衡と対数線形近似について
・【仮定】数式の単純化のために、インフレゼロの定常均衡に達している場合について考える。
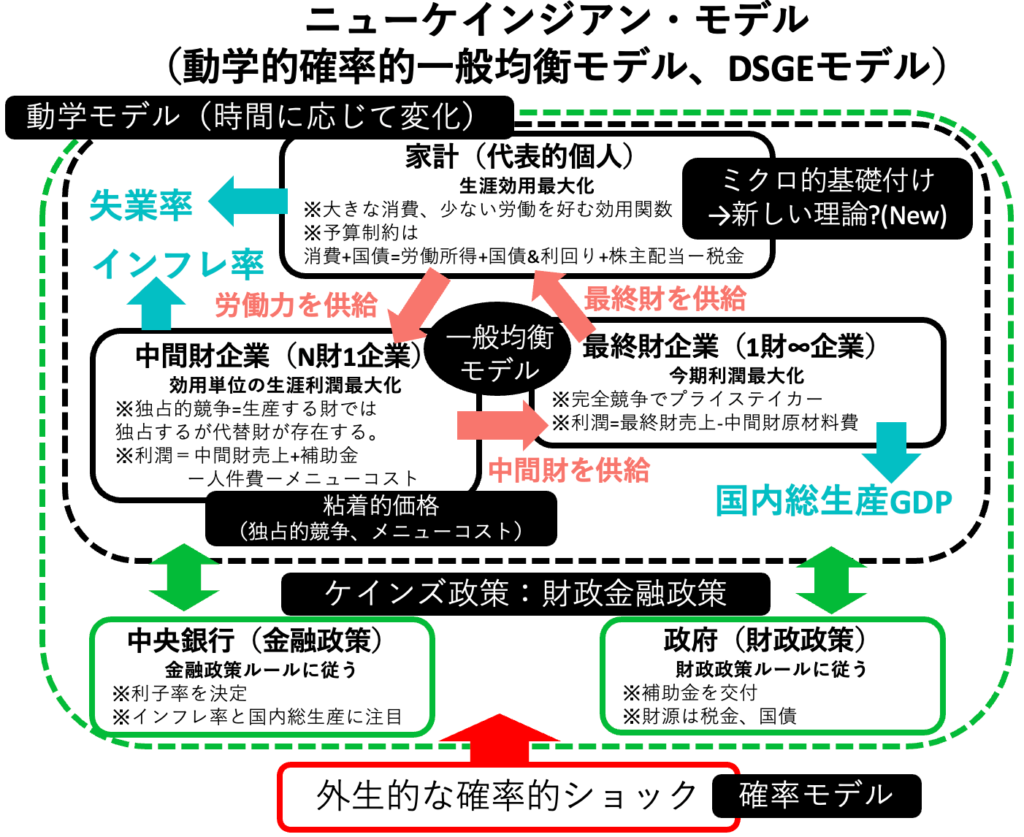
問A:中間財企業1社による独占
問A-1:需要曲線
問A-1:i財を生産している中間財企業1社が直面する中間財iの需要曲線を「ミクロ的基礎について / ニューケインジアン・モデル」を参考に求めよ。(←記事を読まなくても下にメモってある)。ただし、物価変動によって答えが変わること、経済成長によって答えが変わることを避けるために、次の相対量で書け。
$$相対価格p_{i,t}=\frac{P_{i,t}}{P_t}、相対生産量y_{i,t}=\frac{Y_{i,t}}{Y_t}$$
$$需要曲線:Y_{i,t}=\left[ \frac{ P_{i,t}}{P_t} \right]^{-\theta} \frac{Y_t}{N}$$
(解答)
需要曲線を変更して
$$Y_{i,t}=\left[ \frac{ P_{i,t}}{P_t} \right]^{-\theta} \frac{Y_t}{N}$$
$$\frac{Y_{i,t}}{Y_t}=\frac{1}{N} \left[ \frac{ P_{i,t}}{P_t} \right]^{-\theta}$$
$$y_{i,t}=\frac{1}{N} p_{i,t}^{-\theta}$$
問A-2:逆需要関数
問A-2:中間財企業iが、中間財iの市場を独占しているので、中間財価格Piを自社で決定できる。中間財供給量に応じて、需要者の支払意志額が決まるので、それにピッタリと合わせるのがよい。「需要量→価格」という関数は「価格→需要量」という需要関数の逆関数であり、逆需要関数とよばれる。これを求めよ。
(解答)
問A-1より
$$y_{i,t}=\frac{1}{N} p_{i,t}^{-\theta}$$
$$p_{i,t}=\left(N y_{i,t}\right)^{\frac{-1}{\theta}}$$
問A-3:限界収入
問A-3:中間財企業iが限界的に1単位生産量を増やしたときに新しく得られる収入を求めよ。これは限界収入を求める問題である。また、単位は相対量で考えよ。なお、中間財企業iの利潤は以下の通り。ただし、インフレゼロの定常均衡を前提にし、価格調整コストは無視している。
$$中間財企業iの利潤\Phi_{i,t} =P_{i,t} Y_{i,t} -W_t L_{i,t} +g P_{i,t} Y_{i,t}$$
$$中間財企業iの相対利潤\frac{\Phi_{i,t}}{P_t Y_t} $$
(解答)
収入は売上+補助金で
$$収入=P_{i,t} Y_{i,t}+g P_{i,t} Y_{i,t}=(1+g)P_{i,t} Y_{i,t}$$
であるが、相対量に直すと
$$相対収入=\frac{収入}{P_t Y_t} =\frac{(1+g)P_{i,t} Y_{i,t}}{P_t Y_t} =(1+g)p_{i,t}y_{i,t}$$
になる。補足しておくと、物価Pや最終財生産量は中間財企業1社では変えられないので定数とみなせる。
さて、ここで問A-2での逆需要関数を用いると
$$相対収入=(1+g)\left( N y_{i,t}\right)^{\frac{-1}{\theta}}y_{i,t}$$
$$=N^{\frac{-1}{\theta}}(1+g) y_{i,t}^{\frac{\theta-1}{\theta}}$$
よって限界収入MRは
$$MR=\frac{\theta-1}{\theta} N^{\frac{-1}{\theta}}(1+g) y_{i,t}^{\frac{-1}{\theta}}$$
なお、Nは中間財の企業数である。
問A-4:限界費用
問A-4:中間財企業iが限界的に1単位生産量を増やしたときに新しくかかる費用を求めよ。これは限界費用を求める問題である。また、単位は相対量で賃金は実質賃金で考えよ。なお、中間財企業iの利潤は以下の通り。ただし、インフレゼロの定常均衡を前提にし、価格調整コストは無視している。
$$中間財企業iの利潤\Phi_{i,t} =P_{i,t} Y_{i,t} -W_t L_{i,t} +g P_{i,t} Y_{i,t}$$
$$中間財企業iの生産関数:Y_{i,t}= L_{i,t}$$
$$実質賃金w_t=\frac{名目賃金W_t }{P_t}$$
(解答)
費用は人件費のみである。(この段階で指摘しておくと、このモデルでは固定費用がないので、平均費用曲線と限界費用曲線が一致する。)
$$相対費用=\frac{費用}{P_t Y_t} =W_t L_{i,t}=W_t Y_{i,t}=\frac{W_t Y_{i,t}}{P_t Y_t}=w_t y_{i,t}$$
ゆえに
$$限界費用MC=w_t$$
補足しておくと、賃金wは中間財企業1社では変えられないので定数とみなせる。
問A-5:独占
問A-5:相対量を用いて中間財企業の独占行動を求めよ。
(1)独占生産量を求めよ。
(2)独占価格を求めよ。
(3)概略図を書いて、消費者余剰、生産者余剰、死荷重、独占利潤を図示せよ。
(解答)
(1)
独占では限界収入=限界費用が成立する。これは相対利潤についての1階条件をとると導出できる。
$$限界収入MR=限界費用MC$$
$$\frac{\theta-1}{\theta} N^{\frac{-1}{\theta}}(1+g) y_{i,t}^{\frac{-1}{\theta}}=w_t$$
ゆえに
$$N^{\frac{-1}{\theta}} y_{i,t}^{\frac{-1}{\theta}}=\frac{\theta}{(\theta-1)(1+g)}w_t$$
$$N y_{i,t}=\left( \frac{\theta}{(\theta-1)(1+g)}w_t \right)^{-\theta}$$
$$y_{i,t}=\frac{1}{N}\left( \frac{\theta}{(\theta-1)(1+g)}w_t \right)^{-\theta}$$
これが中間財市場iを独占する独占企業iの最適生産量である。
(2)
独占価格を知るには逆需要関数に代入して
$$p_{i,t}=\left(N y_{i,t}\right)^{\frac{-1}{\theta}} \cdots 逆需要関数$$
$$=\left(N \frac{1}{N}\left( \frac{\theta}{(\theta-1)(1+g)}w_t \right)^{-\theta} \right)^{\frac{-1}{\theta}}$$
$$=\left(\left( \frac{\theta}{(\theta-1)(1+g)}w_t \right)^{-\theta} \right)^{\frac{-1}{\theta}}$$
よって
$$p_{i,t}=\frac{\theta}{(\theta-1)(1+g)}w_t $$
(3)
以上の結果をまとめると、次のグラフが描ける。
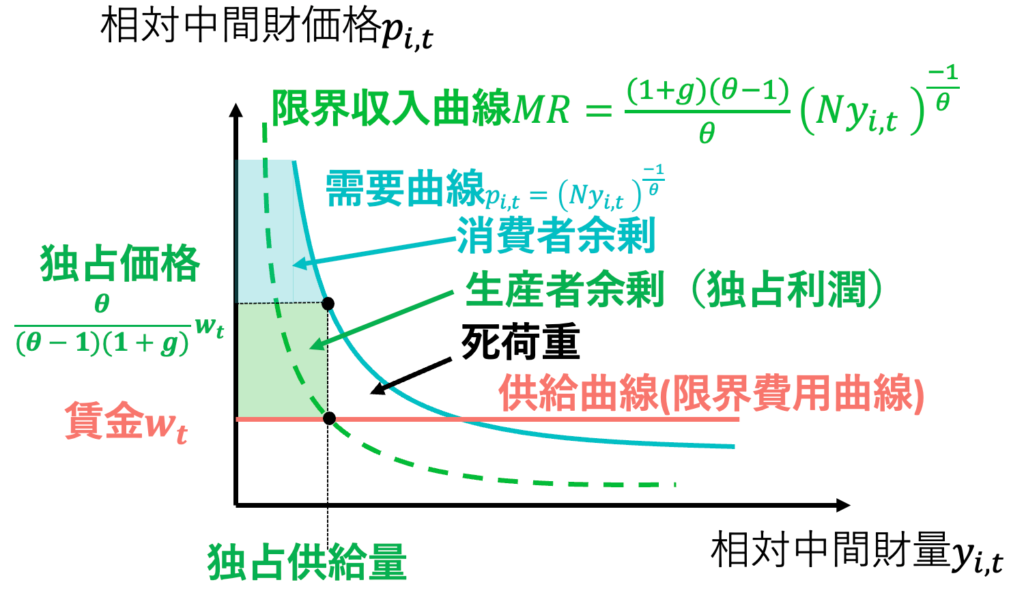
問B:中間財企業N社による独占的競争
問Aでは1社が完全に独占企業として振る舞える場合を扱った。しかし、ニューケインジアン・モデルでは「独占的競争」を扱っている。独占的競争とは
・自社が生産する財における市場では独占企業である。したがって、価格支配力を持つ。
・自社が生産する財は他の財の代替財である。したがって、価格を上げすぎると買い手を失う。
という現実に近い競争形態である。アサヒビール、キリンビール、サントリービールを供給するのはアサヒ、キリン、サントリーのみで自社の価格について価格支配力をもつ。しかし、自社だけが価格を上げすぎると、代替財である他のビールに乗り換えられてしまう。
問B-1:需要者である最終財企業
問B-1:次の問いに答えよ。なお、これは「ミクロ的基礎について / ニューケインジアン・モデル」のB-1と同じであり、答えを書いておいたので、解かずに、問B-2に進んでもよい。
(1)最終財企業は完全競争に直面しており、利潤=0で最終財生産量を決定することを述べよ。
$$P_t Y_t -\sum_{i=1}^N P_{i,t} Y_{i,t}=0 $$
(2)最終財価格を中間財価格で表せ。ただし、中間財価格は独占企業である中間財企業によって操作されている。
$$P_t =N^{\frac{-1}{1-\theta}} \left( \sum_{i=1}^N P_{i,t} ^{1-\theta}\right)^{\frac{1}{1-\theta}}$$
(3)等質な中間財企業は同じ中間財価格、中間財生産量を選択することと(2)の結果を用いて、中間財価格の物価上昇率=最終財価格上昇率=インフレ率になることを述べよ。
$$P_{i,t}=P_t $$
(4)等質な中間財企業は同じ中間財価格、中間財生産量を選択することとCES型生産関数を用いて、中間財生産量を最終財価格で表せ。
$$Y_{i,t}=\frac{1}{N}Y_t$$
(解答)
(1)
最終財企業は完全競争に直面しているので、利潤はゼロである。なぜなら、利潤>0ならば新規参入者が登場し、利潤=0になるまで最終財価格が下落する。逆に利潤<0ならば退出者が発生し、利潤=0になるまで最終財価格が上昇する。つまり
$$P_t Y_t -\sum_{i=1}^N P_{i,t} Y_{i,t}=0 $$
(2)
中間財企業は独占的競争をしているので、中間財価格を釣り上げてくる。そのために、需要のある範囲内で、生産量を調整する。
$$需要:Y_{i,t}=\left[ \frac{ P_{i,t}}{P_t} \right]^{-\theta} \frac{Y_t}{N}$$
したがって、最終財企業の利潤は
$$P_t Y_t -\sum_{i=1}^N P_{i,t} Y_{i,t}=0 $$
$$P_t Y_t -\sum_{i=1}^N P_{i,t} \left[ \frac{P_{i,t}}{P_t} \right]^{-\theta} \frac{Y_t}{N}=0 $$
$$P_t =\frac{1}{N} \sum_{i=1}^N P_{i,t} \left[ \frac{P_{i,t}}{P_t} \right]^{-\theta} $$
$$P_t^{1-\theta} =\frac{1}{N} \sum_{i=1}^N P_{i,t} \left[ \frac{P_{i,t}}{P_t} \right]^{-\theta} $$
$$P_t=N^{-1} \sum_{i=1}^N P_{i,t} ^{1-\theta} $$
$$P_t =N^{\frac{-1}{1-\theta}} \left( \sum_{i=1}^N P_{i,t} ^{1-\theta}\right)^{\frac{1}{1-\theta}}$$
(3)
中間財企業は、利潤の構造、直面する技術制約、需要制約が等しい。等質な中間財企業の意思決定は、同じになる。つまり、
$$P_{1,t}=P_{2,t}=\cdots =P_{i,t} =\cdots= P_{N,t}$$
(2)の結果に代入すると
$$P_t =N^{\frac{-1}{1-\theta}} \left( \sum_{i=1}^N P_{i,t} ^{1-\theta}\right)^{\frac{1}{1-\theta}}$$
$$P_t =N^{\frac{-1}{1-\theta}} \left( N P_{i,t} ^{1-\theta}\right)^{\frac{1}{1-\theta}}$$
$$=N^{\frac{-1}{1-\theta}} N^{\frac{1}{1-\theta}} \left( P_{i,t} ^{1-\theta}\right)^{\frac{1}{1-\theta}}$$
$$= P_{i,t} $$
つまり
$$P_{i,t}=P_t $$
である。よって
$$\frac{P_t }{P_{t-1} }=\frac{P_{i,t } }{ P_{i,t-1} }$$
(4)独占的競争をする等質な中間財企業
中間財企業は、利潤の構造、直面する技術制約、需要制約が等しい。等質な中間財企業の意思決定は、同じになる。つまり、
$$Y_{1,t}=Y_{2,t}=\cdots =Y_{i,t} =\cdots= Y_{N,t} $$
ここで最終財企業のCES型生産関数に(1)の結果を代入すると
$$Y_t=\left(\frac{1}{N}\sum_{i=1}^N (N Y_{i,t}) ^{\frac{\theta – 1}{\theta }} \right)^{\frac{\theta}{\theta -1}}=\left( \frac{1}{N} (N Y_{i,t}) ^{\frac{\theta – 1}{\theta }} \right)^{\frac{\theta}{\theta -1}}=N Y_{i,t}$$
$$Y_{i,t}=\frac{1}{N}Y_t$$
問B-2:独占的競争と一般均衡
問B-2:問B-1を踏まえると、独占的競争をする企業はお互いの行動に対して最適反応になるように行動する。その結果として、実現される独占相対価格、独占相対生産量は何になるのか。
(解答)
$$独占価格p_{i,t}=\frac{P_{i,t}}{P_t}=\frac{P_{t}}{P_t}=1$$
$$独占y_{i,t}=\frac{Y_{i,t}}{Y_t}=\frac{\frac{1}{N}Y_{t}}{Y_t}=\frac{1}{N}$$
問B-3:賃金水準
問B-3:問A-5と問B-2を踏まえると、独占的競争が行われている中間財市場、完全競争が行われている最終財市場の一般均衡の結果として、実質賃金wが決定される。それはいくらか?
(解答)
問A-5より
$$p_{i,t}=\frac{\theta}{(\theta-1)(1+g)}w_t $$
$$y_{i,t}=\frac{1}{N}\left( \frac{\theta}{(\theta-1)(1+g)}w_t \right)^{-\theta}$$
問B-2より
$$p_{i,t}=1、y_{i,t}=\frac{1}{N}$$
したがって、実質賃金は
$$w_t=\frac{(\theta-1)(1+g)}{\theta}$$
である。なお、これは「非線形モデルでの定常均衡について」にて導出した実質賃金と一致する。
問B-4:グラフ
問B-4:以上の結果を踏まえて、グラフを書け。
(解答)

問C:最適財政政策
問C-1:財政政策
問C-1:gとは売り上げに対する補助金である。ではgを操作すると、何が変わるのか。
(解答)
本来は中間財企業に対する売り上げ補助金であったのだが、最終的には限界費用である賃金
$$MC=w_t=\frac{(\theta-1)(1+g)}{\theta}$$
に転嫁される。
問C-2:完全なる自由放任政策の妥当性
問C-2:全く補助金を支給せず、経済に介入しない完全な自由放任政策は、効率的な資源分配を実現するか? なお、代替の弾力性θ>1とする。
(解答)
効率的な資源配分を実現しない。なぜなら、死荷重が必ず発生するから。

問C-3:最適財政政策
問C-3:死荷重がゼロになるような最適な補助金率を求めよ。これが最適な財政政策である。
(解答)
需要曲線と供給曲線の交点で死荷重ゼロのパレート最適な資源分配が実現する。価格は独占価格1で固定であるから、限界費用=実質賃金w=1となるのが最適である。ゆえに
$$w_t=\frac{(\theta-1)(1+g)}{\theta}=1$$
$$\theta=(\theta-1)(1+g)$$
$$\theta-\theta+1=(\theta-1)g$$
$$g=\frac{1}{\theta-1}$$

問C-4:限界費用価格形成原理
問C-4:本問は今までの問題と関係のないミクロ経済学の知識問題である。パレート最適な資源分配を実現するが、補助金の財源をめぐって論争が起きると言われる独占企業の価格形成政策は、どんな政策であり、その政策の名前は何か。また、この記事で導出された最適財政政策との関係は何か。
(解答)
限界費用で価格が形成されるようにする。死荷重がゼロになるが、赤字額を政府が負担する必要がある。これは限界費用価格形成原理と呼ばれる政策である。この記事で導出された最適財政政策とは、限界費用価格形成原理そのものである。
