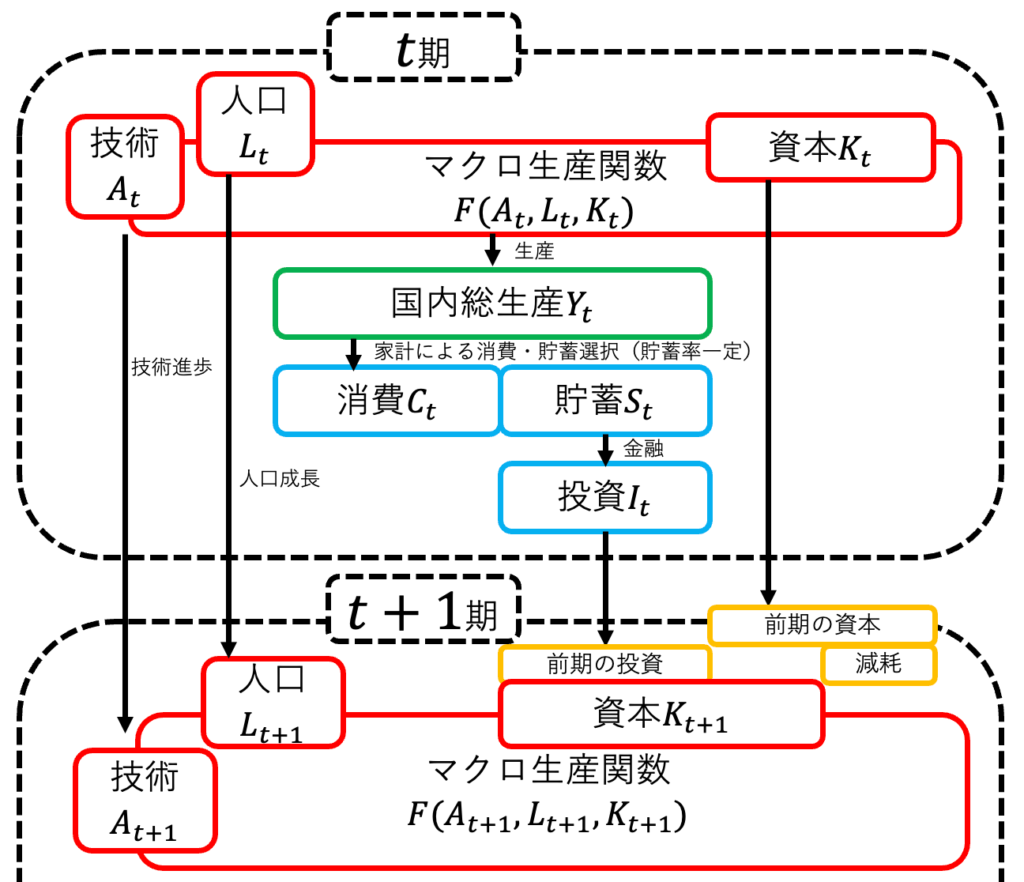
第二次世界大戦後の日本やドイツは、急速な経済発展を遂げた。この経済成長は「定常均衡に至るまでの一時的な高成長」とソロー・モデルで解釈することができる。ソロー・モデルでは、画像1のように国内総生産の一部が投資に費やされる。戦争によって破壊された国には、有望な投資案件が大量に存在する。この状態では、投資効率は非常に高く、急速な資本蓄積に伴う経済成長が生まれうる。
ここで人口成長、技術進歩せず、資本は毎年一定割合で減耗(=故障、摩耗、陳腐化…)するモデルを考える。一人当たり資本で考えてみよう。資本は投資iで増加するが、投資i=貯蓄率s×一人当たり国内総生産yなので、一人当たり資本の増加要因はsf(k)である。一方で、資本は資本減耗率δで減耗すると考えると、一人当たり資本の減少要因はδkである。生産関数f(k)の資本の限界生産性が逓減するなら、画像2のように資本は成長する。
$$資本の増加要因=i_t=s y_t =sf(k_t)$$
$$資本の減少要因=\delta k_t$$
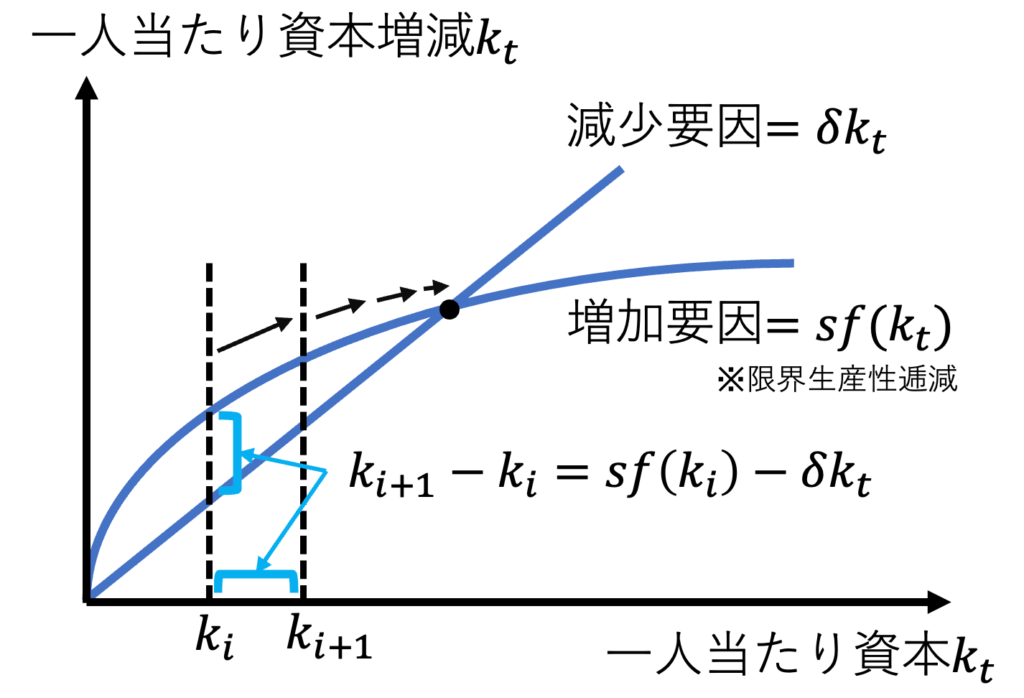
$$sf(k_t)>\delta k_tなら、kは成長$$
$$sf(k_t)=\delta k_tなら、kは停止$$
初期状態によらず、経済は最終的に定常均衡へ到達する。これより、定常均衡は大域的に安定していると表現できる。この記事のモデルでは、一人当たりの資本kが成長しなくなり、経済成長は停止する。これは現実と異なる。そこで、技術進歩と人口成長もするモデルに拡張し、長期的な経済成長が何によって引き起こされるのかを分析しよう。
【追記:モデル】
モデルの詳細は「ソロー成長モデルについて / 経済成長理論」をご覧ください。
【追記:問題】
問:A=1、g=0、n=0と仮定し、一人当たりの経済変数を小文字に表して、以下の問いに答えなさい。
問1:一人当たり資本遷移式(後述)を書け。
$$k_{t+1}=・・・$$
$$ヒント:y_t=\frac{Y_t}{L_t}, f(k_t)=F \left(\frac{K_t}{L_t},1\right )$$
問2:「投資による一人当たり資本の増加」「減耗による一人当たり資本の減少」を縦軸、一人当たり資本を横軸にしたグラフにしなさい。
問3:「投資による一人当たり資本の増加」「減耗による一人当たり資本の減少」が一致する定常均衡において、一人当たりGDPの成長率はいくらになるか答えなさい。
【追記:解答】
人口成長と技術進歩がなければ経済成長しないことを示そう。
問1:一人当たり資本遷移式を書け。
$$A=1、g=0、n=0を仮定する$$
$$次期の資本=今期の資本+今期の投資-今期の資本減耗より$$
$$K_{t+1}=K_t+I_t-\delta K_t$$
$$=K_t+S_t-\delta K_t・・・金融市場均衡条件I_t=S_tより$$
$$=K_t+sY_t-\delta K_t・・・貯蓄率s一定の仮定より$$
$$=sF(K_t,L_t)+(1-\delta )K_t・・・マクロ生産関数より$$
$$ここがポイントなのだが一人当たりに変換する$$
$$一人当たりは小文字で表す。例えばk_t=\frac{K_t}{L_t}$$
$$K_{t+1}=sF(K_t,L_t)+(1-\delta )K_t$$
$$\frac{K_{t+1}}{L_{t}}=\frac{sF(K_t,L_t)}{L_t}+(1-\delta )\frac{K_t}{L_t}$$
$$\frac{K_{t+1}}{L_{t}}\frac{L_{t+1}}{L_{t+1}}=sF \left( \frac{K_t}{L_t},\frac{L_t}{L_t} \right)+(1-\delta )k_t・・・一次同次の生産関数より$$
$$\frac{K_{t+1}}{L_{t+1}}\frac{L_{t+1}}{L_{t}}=sf(k_t)+(1-\delta )k_t・・・f(k_t)=F \left( \frac{K_t}{L_t},1\right)と定義$$
$$k_{t+1}=sf(k_t)+(1-\delta )k_t・・・\frac{L_{t+1}}{L_{t}}=1より$$
問2:「投資による一人当たり資本の増加」「減耗による一人当たり資本の減少」を縦軸、一人当たり資本を横軸にしたグラフにしなさい。
$$一人当たり資本増加k_{t+1}-k_t=[増加sf(k_t)]-[減少\delta k_t]$$

問3:「投資による一人当たり資本の増加」「減耗による一人当たり資本の減少」が一致する定常均衡において、一人当たりGDPの成長率はいくらになるか答えなさい。

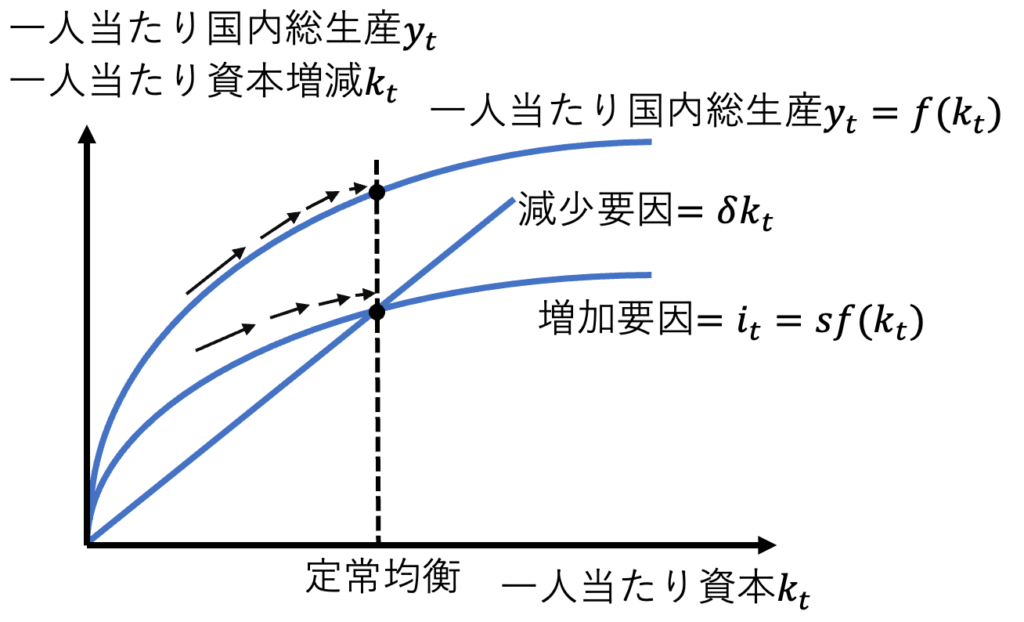
図から明らかなように任意のk_t(>0)について、定常均衡への収束が起る。これを大域的安定性があるという。定常均衡(不動点)が存在し、初期条件によらず、定常均衡が実現するならば、定常均衡を分析することに意味が生まれる。なお、定常均衡の存在と大域的安定性は、マクロ生産関数が限界生産性逓減かつ限界生産性>0という仮定によって実現させられている。
$$定常均衡での一人当たり資本をk^*と表現すると$$
$$k_{t+1}^*-k_t^*=sf(k_t^*)-\delta k_t^*$$
$$sf(k_t^*)-\delta k_t^*=0が定常均衡$$
$$一人当たり資本k_tは一定$$
$$よって、一人当たり国内総生産y_t^*=f(k_t^*)も一定$$
$$したがって、一人当たりGDP成長率はゼロ$$
$$なお、Y_t=y_t L_t=f(k_t^*)L_tも人口成長しないため一定$$
$$したがって、国全体のGDP成長率もゼロ$$
