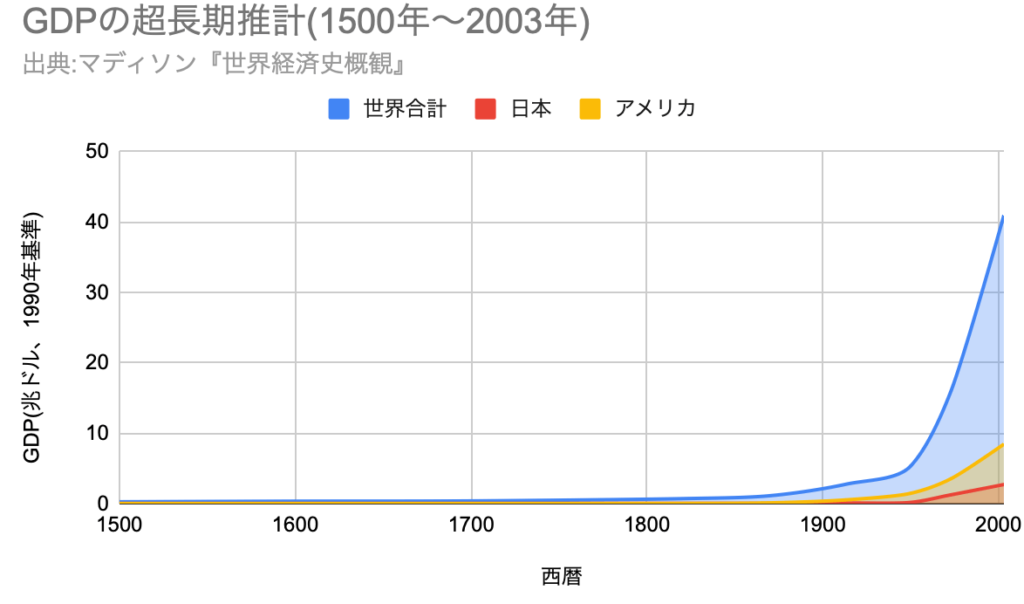
西暦1年から1000年にかけて世界経済は2倍に成長したが、1820年から2003年にかけて世界経済は60倍にまで空前絶後の大発展を遂げた。18世紀のイギリスで産業革命が起こり、人類の生活水準は大幅に向上した。生活水準を決めるのは、長期的には経済成長である。
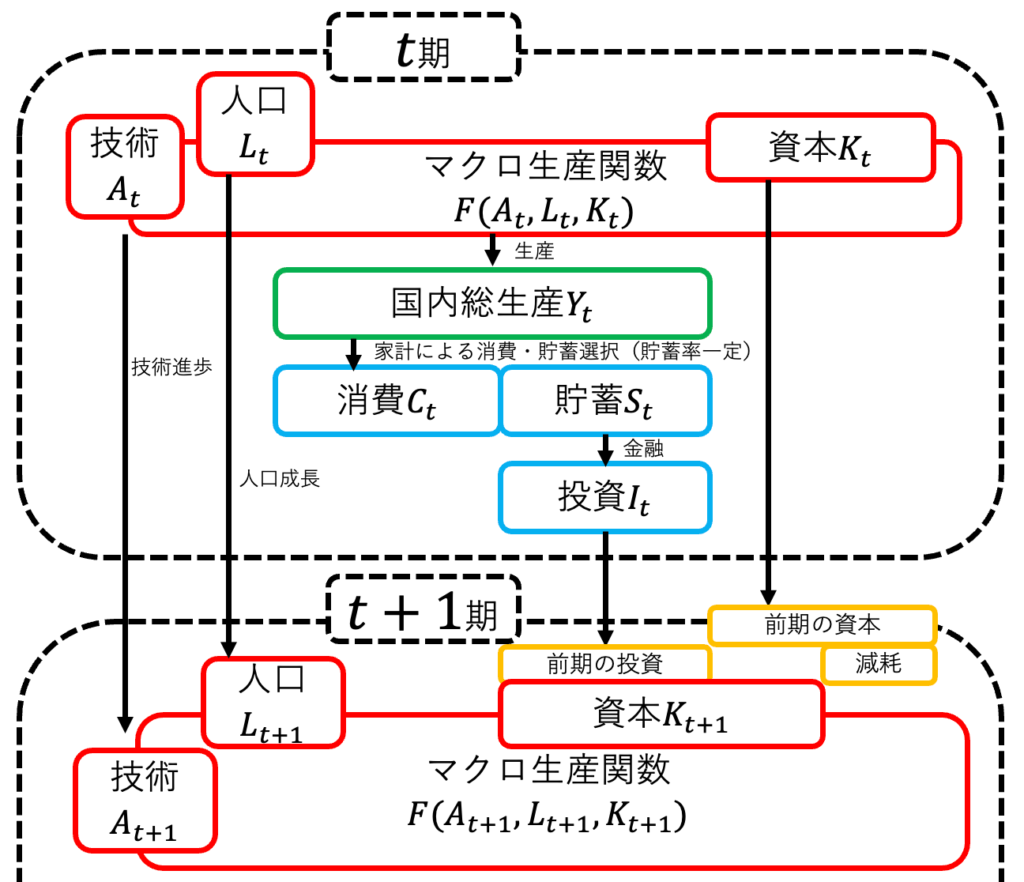
「経済成長がなせ起こるか?」という問いに答えるのが、ソロー・モデルである。ソロー・モデルとは、技術進歩・人口成長・資本蓄積に着目して経済成長を記述するモデルで、他の経済成長モデルや景気循環モデルのベンチマークとなる非常に重要なモデルだ。図にすると、画像2のように表現できる。時間tがどんどん進んでいく。技術水準A、人口L、資本Kによって国内総生産GDPが決定する。GDPは国民の所得となり、消費か貯蓄かに分けられる。貯蓄は、金融機関を通じて、投資となる。投資は、資本を増やす。次の期における資本は、前期の資本+投資ー固定資本減耗によって決定される。この間に、技術進歩や人口成長が起こる。そして、新しい生産活動が始まる。このサイクルが続いていくのが、ソロー・モデルである。
先取りするとソロー成長モデルの結論は「長期的には、一人当たりGDP(=生活水準)の成長率は、技術進歩率に収束する」「長期的には、GDP(=国力)の成長率は技術進歩率と人口成長率の和に収束する」である。「産業革命以来の経済成長は科学技術によるもの」という通念と整合的だ。最近は「科学万能」と言われる時代ではないが、科学が人類の生活水準を決定づけたのは改めて認識しておくべきだ。理系ガンバレ!
本文は以上。以下は付録。
経済成長論の全体像
・「よりよい社会のための経済学入門」>「経済成長 〜ソロー・モデル〜」
第一部:暫定的な結論
・【理論分析】国民の生活水準(=一人当たりGDP、一人当たり消費)を上げるには、技術進歩のみが長期的に重要。
・【理論分析】国の経済力(=GDP)を上げるには、技術進歩と人口成長のみが長期的に重要。
・【政策的示唆】技術進歩が重要である。ただし、実施すべき政策は不明。なぜなら、ソローモデルにて技術進歩は外生的に決まるので、技術進歩を発生させる政策について考察できないからである。
第二部:モデル
第1回:ソロー成長モデルについて(この記事)
第三部:事実解明的な分析
第2回:短期的な経済成長の要因について
第3回:長期的な経済成長の要因について
第四部:規範的な分析
第4回:経済成長の黄金律について
第5回:完全分配定理について
第6回:資本所得と労働所得の成長について
第五部:付録
第7回:成長会計について
第8回:景気循環について
問A:ソロー・モデルの数式
ソロー・モデルを味わおう。
問A-0:要約
問A-0:問A-1から問A-6の解答を要約すると、ソロー・モデルはどう表現できるか。
(解答)
せっかちな人用に要約版のソローモデルを載せておく。けれども、これでは経済学的な解釈が不足しているので、問A-1から問A-6も読んでほしい。
$$国内総生産:Y_t=F(K_t,A_t L_t)$$
$$資本蓄積式:K_{t+1}=s Y_t+(1-\delta) K_t$$
$$人口成長:L_{t+1}=(1+n)L_t, 技術進歩:A_{t+1}=(1+g)A_t$$
ただし、マクロ生産関数は次の条件を満たす。
$$正の限界生産性:\frac{\partial F}{\partial K}>0,\frac{\partial F}{\partial L}>0$$
$$限界生産性逓減:\frac{\partial^2 F}{\partial K^2} <0,\frac{\partial^2 F}{\partial L^2} <0$$
$$規模に対して収穫一定:F(\lambda K, \lambda AL)=\lambda F(K, AL)$$
$$例えば、コブ=ダグラス型生産関数K_t^\alpha (A_tL_t)^{1-\alpha}がこれらの条件を満たす。$$
アルファベットの定義は「t:離散的な時間。time」「Y:国内総生産。Yield」「F:マクロ生産関数。Function」「K:資本。Kapital(ドイツ語)」「A:技術水準。Art」「L:労働(=人口)。Labor」「I:投資。Investment」「S:貯蓄。Saving」「g:技術進歩率。Growth」「n:人口成長率。Number」「δ:固定資本減耗率。fixed capital Depreciation rate)。また、モデルを解く際は「効率労働:AL」とし、効率労働一単位当たりの資本、生産関数などを小文字で表すことが多い。例えば、k=K/AL、f(k)=F(K/AL,1)。
問A-1:家計
問A-1:家計の行動を定式化せよ。家計は、所得Yを毎年定率で消費Cや貯蓄Sを行う。また、このような消費関数をなんと呼ぶか。
(解答)
sを貯蓄率とすると、家計は
$$消費:C_t=(1-s)Y_t$$
$$貯蓄:S_t=sY_t$$
のように消費、貯蓄の選択を行う。このような消費関数をクズネッツ型消費関数といい、ケインズ型消費関数とは異なる。
問A-2:企業
問A-2:企業の行動を定式化せよ。企業は、資本K、労働L、技術水準Aを用いて生産Yを行う。企業の生産関数は、次の仮定を満たす。
・仮定1:限界生産性は正。生産要素を増やせば生産量は必ず増える。
・仮定2:限界生産性逓減。生産要素を増やせば、「増える生産量」は必ず減っていく。
・仮定3:規模に対して収穫一定。例えば、資本Kと労働Lを2倍にしたら、生産性変わらず、生産量Yは2倍。
・仮定4:ハロッド中立型技術進歩が発生する。このとき、生産関数は
$$ハロッド中立的技術進歩の生産関数F(K_t,A_t L_t)$$
と表せることが知られている。また、これらの条件を満たす代表的な生産関数を例示せよ。
(解答)
企業は、資本K、労働L、技術水準Aを用いて
$$国内総生産Y_t=F(K_t,A_tL_t)$$
という生産活動を行う。ただし、この生産関数は
$$限界生産性は正:\frac{\partial F}{\partial K}>0,\frac{\partial F}{\partial L}>0$$
$$限界生産性逓減:\frac{\partial^2 F}{\partial K^2} <0,\frac{\partial^2 F}{\partial L^2} <0$$
$$規模に対して収穫一定:F(\lambda K, \lambda AL)=\lambda F(K, AL)$$
という条件を満たす。このような生産関数の例として、次のコブ=ダグラス型生産関数
$$F(K_t,A_tL_t)=K_t^\alpha (A_tL_t)^{1-\alpha}$$
が挙げられる。なお、ソロー・モデルの結論を得るためには仮定1〜仮定4が成り立てばよく、コブ=ダグラス型生産関数である必要はない。
問A-3:資本蓄積
問A-3:資本蓄積をモデル化しよう。t+1期の資本は、t期の資本Kとt期の投資Iを足して、t期の固定資本減耗を引いたものである。また、固定資本減耗率δは、一定と考えよ。
(1)資本蓄積を定式化せよ。つまり、資本遷移式、資本の動学方程式を求めよ。
(2)固定資本減耗とは何か。現実世界における会計処理と関係づけて説明せよ。
(3)ソロー・モデルでは、企業は資本を使用する際に、どんな費用を負担するか。
(4)(3)を踏まえて、t期の企業の利潤最大化行動を定式化せよ。
(解答)
(1)
$$資本遷移式:K_{t+1}=K_t+I_t-\delta K_t$$
(2)
固定資本減耗とは、工場、建物、車両、コンピューターといった資本が故障、摩耗、陳腐化によって価値を失うことである。
現実世界では、固定資本減耗は、減価償却と呼ばれる会計処理がなされる。決算において、減価償却費として費用計上され、減価償却累計額として資産の控除項目となる。なお、ソロー・モデルでは、定率法で減価償却している。定額法の減価償却と解釈するならば、すべての資本の耐用年数=1/δと解釈できる。
(3)
企業は資本を使用する際に、資本の所有者である資本家に資本レンタル料(=利子)を払うと同時に、固定資本減耗費を負担する。
では、固定資本減耗費は誰に支払われているのだろうか? 一つの解釈として、固定資本減耗費とは、物理法則の所有者である神が、物理法則の使用者である人間に代償を要求し、人間がその代償を貨幣ではなく実物で支払っていると考えることができる※。
※固定資本減耗費=神への貢物説は、しまうま総研オリジナルな考え方であり、他では通用しないので注意。
※一般に、資本の使用者費用=利息+減価償却費+固定資本評価損である。
(4)
利潤は、収益ー費用である。収益はマクロ生産関数、費用は資本レンタル料、固定資本減耗費、人件費である。
ゆえに、企業の利潤最大化行動は
$$\max_{K_t,L_t} F(K_t,A_t L_t)-(r_t+\delta)K_t-w_t L_t$$
となる。なお、GDPと同一視されているマクロ生産関数はすでに貨幣単位であるので、ミクロ経済学のように前に価格Pを付けなくて良い。
問A-4:人口成長
問A-4:人口は、一定の人口成長率nで成長する。なお、人口のすべてが労働者Lであると考える。
(1)定式化せよ。
(2)このような人口成長を危険視した人物にマルサス(1766年 – 1834年)がいる。マルサスはなんと述べたか。また、マルサスの懸念はソロー・モデルで実現するか?
(解答)
(1)
$$人口成長:L_{t+1}=(1+n)L_t$$
(2)
マルサスは「人口は制限されなければ、指数関数的に増加するが、生活資源は直線的にしか増加しないので、生活資源は必ず不足する」と主張した。マルサスは人口増加による社会の貧困化を懸念したのである。
マルサスの懸念はソロー・モデルで実現しない。ソロー・モデルでは、指数関数的に人口が増大しても、資本蓄積と技術進歩のために、生活水準はむしろ向上する。
問A-5:技術進歩
問A-5:技術水準Aは、一定の技術進歩率gで成長する。
(1)定式化せよ。
(2)ソロー・モデルでは技術進歩は外生的に(=モデルの外で)決まる。では、技術進歩が内生的に(=モデルの中で)決まる理論をなんと呼ぶか。
(解答)
(1)
$$技術進歩:A_{t+1}=(1+g)A_t$$
(2)
技術進歩が内生的に決まるモデルを、内生的経済成長理論と呼ぶ。重要な研究領域である。
問A-6:市場均衡条件
問A-6:すべての市場が均衡する。これについて説明せよ。
(1)財市場均衡条件を定式化せよ。さらに、三面等価の原則を踏まえて説明せよ。
(2)金融市場均衡条件を定式化せよ。
(3)労働市場均衡条件を定式化せよ。
(解答)
三面等価の原則によれば
・生産面のGDP=国内総生産Y
・支出面のGDP=消費C+投資I+政府支出G+輸出EX-輸入IM
・分配面のGDP=労働所得+(総)資本所得+間接税ー補助金
※総資本所得=純資本所得+固定資本減耗
の3つが一致する。ただし、ソロー・モデルでは、政府部門と海外部門を考慮していないので、
$$供給Y_t=需要C_t+I_t=所得w_tL_t+r_t K_t+\delta K_t$$
が成立する。財市場均衡条件とは、
$$Y_t=C_t+I_t$$
である。
(2)
$$所得Y_t=消費C_t+貯蓄S_t$$
$$生産Y_t=消費C_t+投資I_t$$
より、金融市場の均衡条件とは
$$資金供給S_t=資金需要I_t$$
である。企業が利潤最大化行動と取ることで、投資Iは利子率rに応じて変化し、ISバランスが実現する。
(3)
労働市場の均衡条件とは
$$労働供給L_t=労働需要L_t$$
である。企業が利潤最大化行動と取ることで、労働需要は賃金wに応じて変化し、人口とバランスする。
問B:ソロー・モデルの経済学的な位置付け
問B:ソロー・モデルとは、経済学史的にどのようなものか。
(1)ソロー・モデルの名称をいくつか挙げよ。また、その由来を説明せよ。
(2)ソロー・モデルにおいて最も重要な結論は何か。
(3)ソロー・モデルに欠けている経済学的に重要な要素は何か。
(解答)
(1)
・ソロー・モデル(Solow model):ロバート・ソローが1956年に発表したことに由来する。
・ソロー成長モデル(Solow growth model):ロバート・ソローの経済成長モデルであることに由来する。
・ソロー=スワン・モデル(Solow–Swan model):1956年にロバート・ソローとトレイバー・スワンが発表したモデルであることに由来する。
・新古典派経済成長モデル(Neoclassical Growth Model):新古典派と呼ばれる経済学者たちの代表的な経済成長モデルであることに由来する。
(2)
ソロー・モデルにおいて最も重要な結論は「長期的には一人当たりGDPの成長率は技術進歩率に収束する」である。技術進歩が生活水準を決定することを意味する。
(3)
ソロー・モデルには、ミクロ的基礎がない。つまり、消費者や企業の最適化行動が組み込まれていない。
問C:データ分析とソロー・モデルの整合性
問C:ソロー・モデルと現実との関係はどのようになっているのか。
(1)カルドア(1961)の経済成長についての6つの定型化された事実(Stylied Facts)を説明せよ。
(2)ソロー・モデルはカルドアの6つの定型化された事実をどのように説明するか。
(3)ロバート・ソロー(1957)はどのような実証分析を行なったか。
(解答)
(1)
カルドアは1961年に経済成長に関する基本的な事実として次の6つを指摘した。
・第一に、国内生産量Yと労働生産性Y/Lは、継続的に成長している。
・第二に、労働者一人当たりの資本K/Lは、継続的に成長している。
・第三に、資本から得られる利益率は、ほぼ一定である。
・第四に、国内総生産と資本の成長率は、ほぼ同一である。
・第五に、労働分配率や投資比率I/Yは、ほぼ一定である。
・第六に、国内生産量Yと労働生産性Y/Lの成長率は、国によって差がある。
(2)
ソロー・モデルは、カルドアの6つの定型的な事実のうち、最初の5つを説明できる。
・第一に、国内生産量Yと労働生産性Y/Lは、継続的に成長している。→Yの成長率は、技術進歩率と人口成長率の和。労働生産性Y/Lの成長率は、技術進歩率。
・第二に、労働者一人当たりの資本K/Lは、継続的に成長している。→K/Lの成長率は、技術進歩率。
・第三に、資本から得られる利益率は、ほぼ一定である。→定常利子率rは一定。
・第四に、国内総生産と資本の成長率は、ほぼ同一である。→Yの成長率とKの成長率は、技術進歩率と人口成長率の和。
・第五に、労働分配率や投資比率I/Yは、ほぼ一定である。→労働分配率はコブ・ダグラス型生産関数のパラメーターで一定。投資比率I/Yとは貯蓄比率S/Yであるので、投資比率I/Yは貯蓄率で一定。
・第六に、国内生産量Yと労働生産性Y/Lの成長率は、国によって差がある。→スタンダードなソロー・モデルでは、長期的にはすべての国は同一の生活水準を実現するため説明できない。表面上は同一の生活水準ではないが、教育水準などをコントロールすると同一の経済が実現しているという「条件付き収束」という考え方はある。
(3)
ロバート・ソローは1957年に成長会計(Growth Accounting)という手法で「労働者一人当たりの米国の生産量の増加の約5分の4が技術の進歩に起因する」と計算し、技術進歩の重要性を主張した。
