「あの人にはバイアスがかかっている」「世の中を色メガネで見ている」「考え方が偏っている」「考え方の癖が強い」。これらはバイアスに関する表現である。しかし、バイアスとは何かを問われるとなかなか答えづらい。
そこで、統計学の概念をヒントにしよう。統計学では、推定量にバイアスがないことを不偏性(unbiasedness)と言う。統計学は母集団のパラメーターθを知ろうとするが、標本から推定するしかない。パラメーターが推定量の期待値と等しいとき、その推定量には不偏性があるという。例えば、パラメーターが80で、赤と青の推定量を用いて推定するとしよう。図1のように分布するならば、赤の推定量には不偏性があり、青の推定量には不偏性がない。
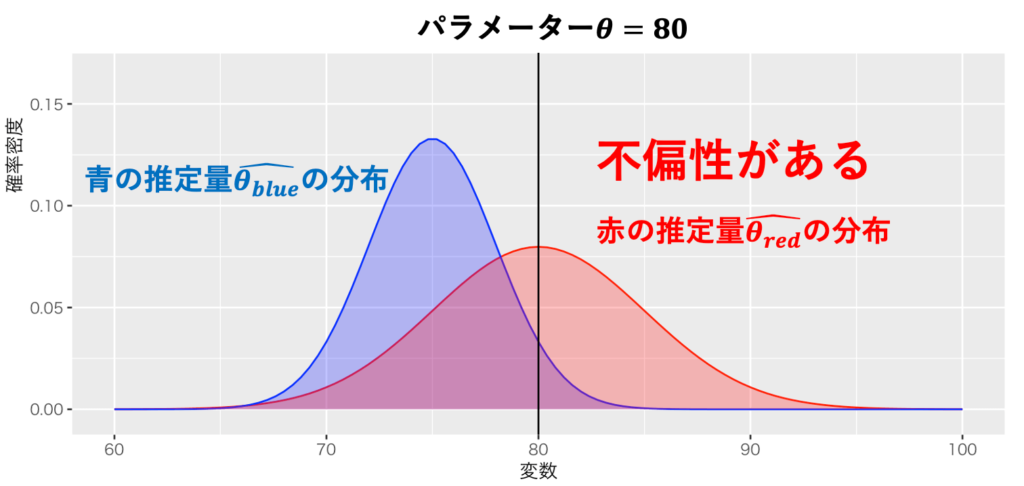
出典:しまうま総研(2023)
解説:コードは付録に掲載
$$不偏性の定義:E \left( \widehat{ \theta} \right)= \theta$$
$$\theta:パラメーター(確定変数)$$
$$\widehat{\theta}:\thetaの推定量(確率変数)$$
$$E \left( \widehat{ \theta} \right):\thetaの推定量の期待値(確定変数)$$
「バイアスがない」=「間違っていない」ではないことに注意すべきだ。「バイアスがない」=「間違い方に規則性がない。ゆえに、思考が平均的に正しい」である。パラメーターを真理、推定量を思考と読み替えて、不偏性を解釈すると、このように解釈することができる。
$$バイアス=E \left( \widehat{ \theta} \right)-\theta=0 平均的に正しい$$
$$誤差=\widehat{ \theta}-\theta=0 正しい$$
【追記】
作図はRを用いて次のコードで実行した。
library(ggplot2)
ggplot(data = data.frame(X = c(60, 100)), aes(x = X))+
stat_function(fun = dnorm, args = list(mean = 80,sd = 5), color="red")+
stat_function(fun = dnorm, args = list(mean = 75,sd = 3), color="blue")+
scale_y_continuous(limits=c(0,0.25))+
xlab("変数")+
ylab("確率密度")+
geom_ribbon(data=data.frame(X=x<-seq(60,100,len=101), Y=dnorm(x,mean=75,sd=3)), aes(x=X, ymin=0, ymax=Y),fill="blue",alpha=0.3)+
geom_ribbon(data=data.frame(X=x<-seq(60,100,len=101), Y=dnorm(x,mean=80,sd=5)), aes(x=X, ymin=0, ymax=Y),fill="red",alpha=0.3)+
theme_grey(base_family = "HiraKakuPro-W3")+
geom_vline(xintercept =80 )