ロジスティック回帰モデル(logistic regression model)は、潜在変数で解釈する際、誤差項がロジスティック分布に従い、入力は重回帰モデルと同じ線形なモデルだが、出力が0か1という統計モデルである。潜在変数Y*≦0のときY=0、潜在変数Y*>0のときY=1を出力する。
$$目的変数Y=\begin{cases} 0 (Y^*≦0) \\ 1 (Y^*>0) \end{cases}$$
$$潜在変数 Y^*=\beta_0 + \beta_1 X_1 +\cdots +\beta_k X_k +U$$
$$U|X_1,X_2 \cdots X_k が標準ロジスティック分布※に従う$$
$$※ 累積分布関数=\frac{e^x}{1+e^x} E(X)=0、Var(X)=\frac{\pi^2}{3}$$
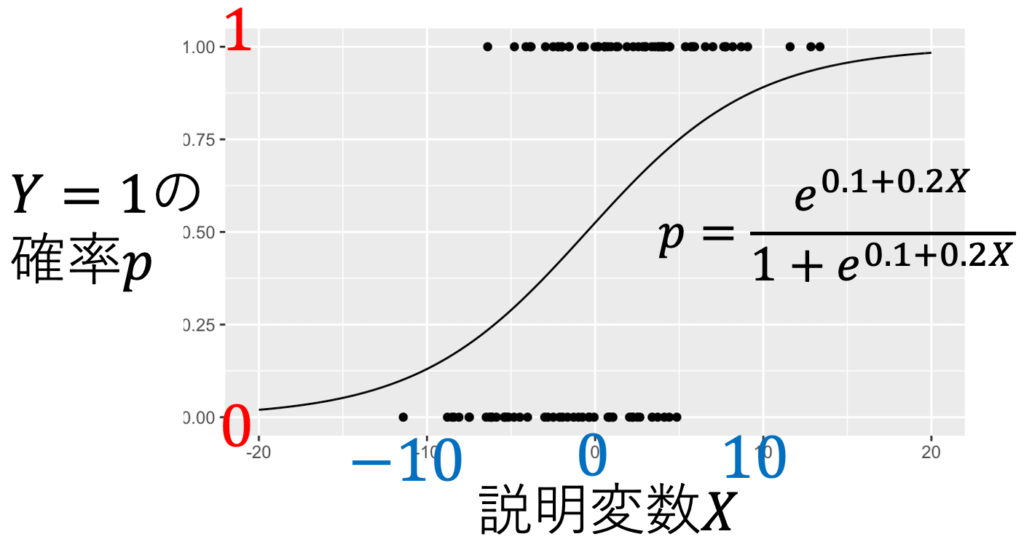
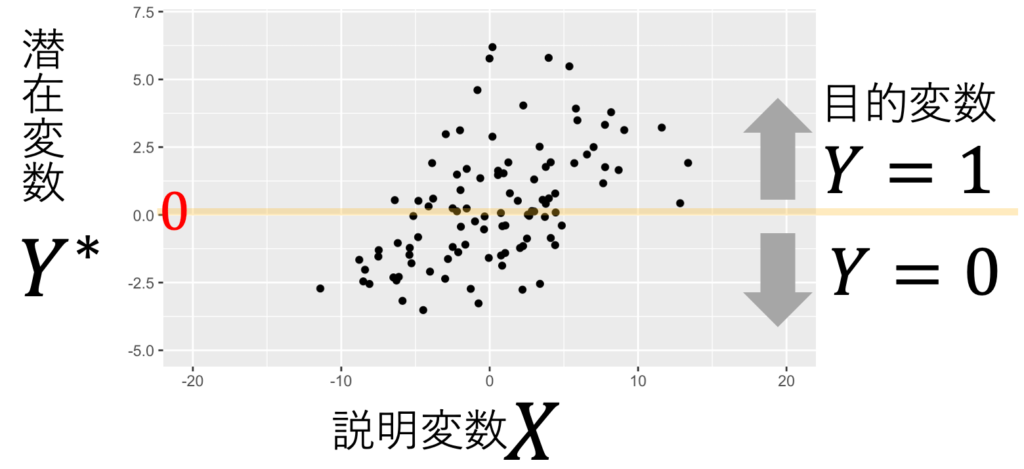
潜在変数モデルからY=1になる確率P(Y=1)を求められる。それが下の式である。説明変数が1つで、β0=0.1、β2=0.2のモデルで標本を乱数発生させた結果が、図1だ。図1からは、いくらXが大きくとも、Xが小さくとも確率pは0以上1以下という確率の性質をもっている。図2は、この標本になる際に発生させた潜在変数Y*である。
$$P(Y=1)=\frac{e^{(\beta_0 + \beta_1 X_1 +\cdots +\beta_k X_k)}}{1+e^{(\beta_0 + \beta_1 X_1 +\cdots + \beta_k X_k)}}$$
出典:しまうま総研(2023)が作成
補足:Rコードは追記に載せた。
出典:しまうま総研(2023)が作成
補足:Rコードは追記に載せた。
潜在変数モデルの枠組みは面白い。潜在変数モデルとは、見えない潜在変数が、見える目的変数に変換されて、現象となる世界観だ。そして、ロジスティック回帰モデルの仮定も、明瞭になる。誤差項の条件付き分布が標準ロジスティック分布と従うことは、外生性、均一分散、分布の形状指定が仮定されていることを意味する。均一分散、分布の形状指定の仮定が必要ない重回帰分析より、ロジスティック回帰分析の方が仮定が多いし、ロジスティック回帰分析でも外生性に気配りしないといけないのは同じだ。
【追記】
ロジスティック回帰モデルのパラメーター推定は次のRコードで実行できる。logitは、ロジスティック回帰モデルのリンク関数がロジット関数と呼ばれることに由来する。なお、計量経済学ではロジスティック回帰モデルをロジット・モデルと呼んだりする。
glm(y ~ x1 + x2 ,data=Data, family=binomial(link=logit)) #ロジスティック回帰モデル潜在変数モデルからP(Y=1)の確率を導こう。ロジスティック分布の累積分布関数は、記事冒頭に記した。
$$P(Y=1)=P(Y^*>0) 潜在変数モデルより$$
$$=1-P(Y^*≦0)$$
$$=1-P(\beta_0 + \beta_1 X_1 +\cdots +\beta_k X_k +U≦0)$$
$$=1-P(U≦-\beta_0 – \beta_1 X_1 -\cdots -\beta_k X_k) $$
$$=1-\frac{e^{(-\beta_0 – \beta_1 X_1 -\cdots -\beta_k X_k)}}{1+e^{(-\beta_0 – \beta_1 X_1 -\cdots -\beta_k X_k)}} 累積分布関数より$$
$$=\frac{1}{1+e^{(-\beta_0 – \beta_1 X_1 -\cdots -\beta_k X_k)}} ここで終わらせてもよい$$
$$ =\frac{e^{(\beta_0 + \beta_1 X_1 +\cdots +\beta_k X_k)}}{1+e^{(\beta_0 + \beta_1 X_1 +\cdots + \beta_k X_k)}} 求まった!$$
作図のためのRコードをつけておく。
#ggplot2の呼び出し
library(ggplot2)
#ロジスティック回帰モデル
p <- function(x) (exp(1)^(0.1+0.2*x))/(1+(exp(1)^(0.1+0.2*x)))
#潜在変数モデルでの標本生成
sample_size <- 100
x <- rnorm(n=sample_size, mean =-0.5, sd=5)
u <- rlogis(sample_size)
yy <- 0.1 + 0.2*x+ u #潜在変数yyを作る
y <- ifelse(yy>=0,1,0) # 0を以上なら1、未満なら0の二値変数yを作る
data_L <- data.frame(x,y,yy)
#図1の描画
ggplot(data_L,aes(x =x, y=y))+
geom_point()+
stat_function(fun=p)+
scale_x_continuous(limits = c(-20, 20))+
scale_y_continuous(limits = c(0, 1))
#図2の描画
ggplot(data_L,aes(x =x, y=yy))+
geom_point()+
scale_x_continuous(limits = c(-20, 20))+
scale_y_continuous(limits = c(-5, 7))