差の差分析(DID:Difference in Difference)は、パネルデータを用いた因果推論の手法として有名だ。処置群と対照群の2群、2期間のデータがあれば、推定は簡単に実行できる。アイデアは、とても印象的だ。ルービンの因果モデルによれば、因果効果とは事実と反事実の差である。しかし、反事実は観測できないから、反実仮想するしかない。そこで、処置群と共通トレンドをもつ対照群を見つけてきて、反事実を推定する。この処置群の平均処置効果ATTは、差の差(DID)と等しい。
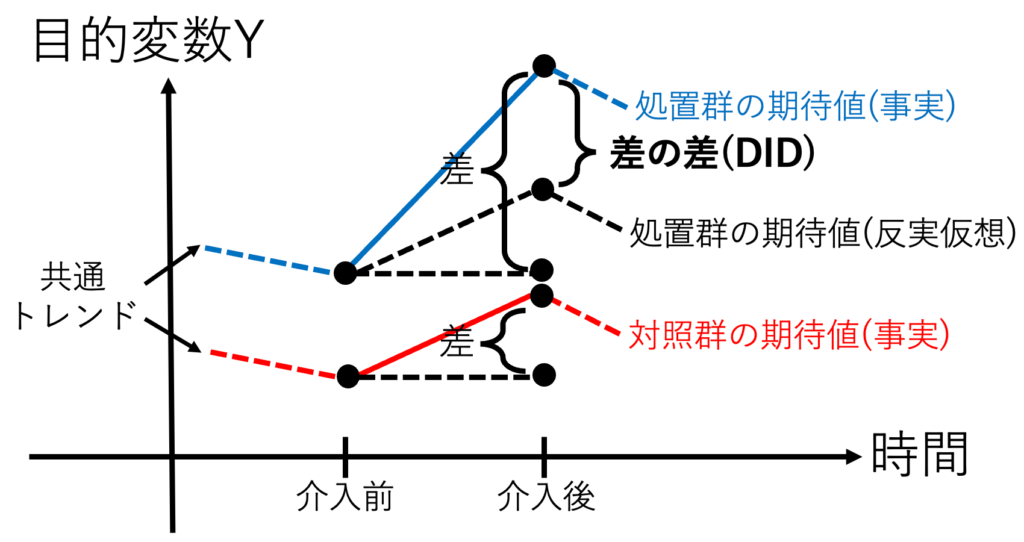
出典:しまうま総研(2023)が作成
このDID推定だが、交互作用モデルの重回帰モデルに帰着させることができる。処置群ダミーとは、処置群なら1、対照群なら0のダミー変数である。介入後ダミーとは、介入後なら1、介入前なら0のダミー変数である。
$$Y=\beta_0+\beta_1 (D_{処置群ダミー})$$
$$+\beta_2 (D_{介入後ダミー})+\beta_3 (D_{介入後ダミー})(D_{処置群ダミー})+U$$
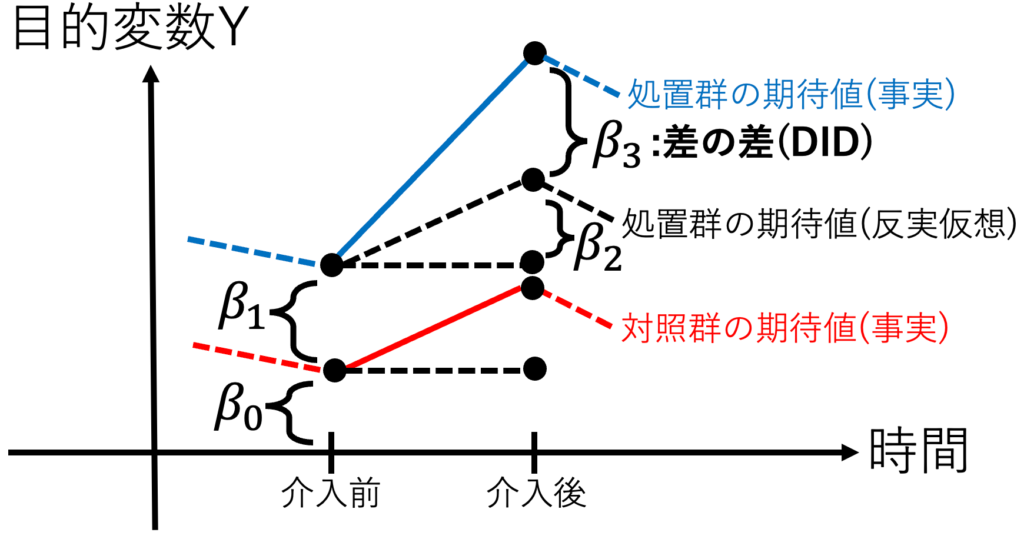
出典:しまうま総研(2023)が作成
共通トレンドをもつ対照群があるのならば、ぜひ差の差法を使いたい。問題は「介入前から共通トレンドが存在する」「介入前後に共通トレンドから外れるような事象が起きていない」の2点が満たされる対照群をどう見つけるかである。
【追記】
・標準誤差について:差の差法では、クラスター構造に頑健な標準誤差を用いるべきだ。
・差の差法での重回帰分析のシミュレーションについて:
次の母集団モデルを考える。
$$Y=40+10(D_{処置群ダミー})$$
$$+5 (D_{介入後ダミー})+10 (D_{介入後ダミー})(D_{処置群ダミー})+U$$
次の標本が生成された。なお、介入後ダミーは0か1だが、それだと点が一直線に並んでしまうので、横方向に散らばせた。
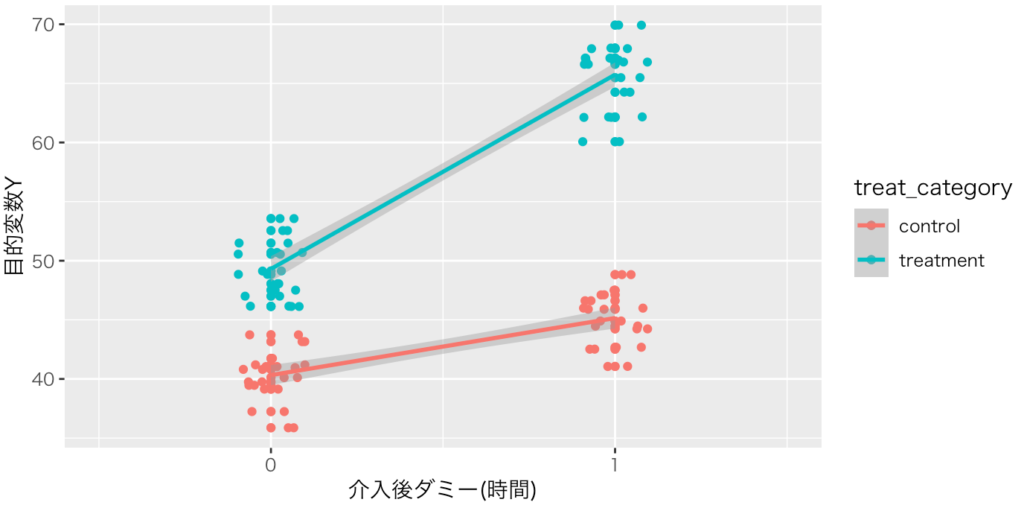
出典:しまうま総研(2023)が作成
解説:コードは追記に掲載
次のコードで推定した結果が、次の通り。差の差(DID)は11.6(95%信頼区間CIは8.99〜14.21)で、母集団の10と近かった。なお、標準誤差はクラスター構造に頑健な標準誤差を用いている。
library(estimatr)
did <- lm_robust(y ~ treat + time +time*treat,
clusters = cluster_id, se_type = "stata",
data = Data)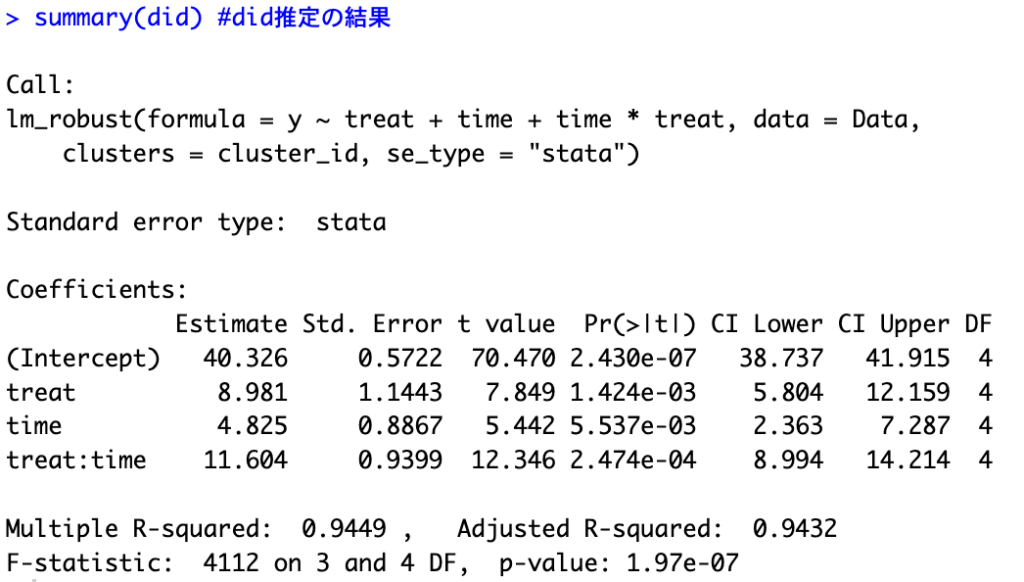
出典:しまうま総研(2023)が作成
解説:コードは追記に掲載
描画と推定に使用したRコードは以下の通り。
#使用するパッケージ
library(estimatr)
library(ggplot2)
#標本の作成
personal_id <- rep(c(1:25),2)
cluster_id <- rep(c(rep("A",5),rep("B",5),rep("C",5),rep("D",5),rep("E",5)),2)
time <- c(rep(0,25),rep(1,25))
treat <- rep(c(0,1),50)
treat_category <- rep(c("control","treatment"),50)
u<- rnorm(n=50, mean =0, sd=3)
y <- 40 + 10*treat + 5*time + 10*time*treat + u
Data <- data.frame(personal_id,cluster_id,time,treat,y,treat_category)
#差の差推定(クラスター構造に頑健な標準誤差を使用)
library(estimatr)
did <- lm_robust(y ~ treat + time +time*treat,
clusters = cluster_id, se_type = "stata",
data = Data)
summary(did)
#作図
library(ggplot2)
ggplot(Data,aes(x =time, y=y,color = treat_category,stat =treat_category ))+
geom_point()+
geom_jitter(width = 0.1)+
stat_smooth(method = "lm", formula='y~x', se = TRUE)