回帰係数βが説明変数Xによって変化する場合は、交互作用モデル(interaction model)を使おう。具体的には、重回帰モデルに交差項(interaction term)を入れれば、よい。その最も単純なモデルが下のモデルである。説明変数X1が1増えたときの限界効果は、X2によって変化する。
$$モデル Y=\beta_0+\beta_1 X_1 +\beta_2 X_2 +\beta_3 X_1 X_2+U$$
$$=\beta_0+(\beta_1 +\beta_3 X_2)X_1 +\beta_2 X_2+U$$
$$限界効果 \frac{\partial Y}{\partial X_1}=\beta_1 +\beta_3 X_2$$
交差項に入る変数がダミー変数の場合、カテゴリごとのパラメーターの差を明らかにすることができる。例えば、男女賃金格差のモデリングができる。男ダミーDと労働時間の交差項を入れることで、男女の時給差がβ3として組み込まれた交互作用モデルを作ることができる。この交互作用モデルは、図1のように表せる。標本例をシミュレーションで作成したのが図2である。
$$男ダミー変数:D_{男}=男性なら1、女性なら0$$
$$交互作用モデル 月収=\beta_0+\beta_1 D_{男}+\beta_2 労働時間+\beta_3 労働時間 D_{男}+U$$
$$=\beta_0+\beta_1 D_{男}+ (\beta_2+\beta_3 D_{男})労働時間+U$$

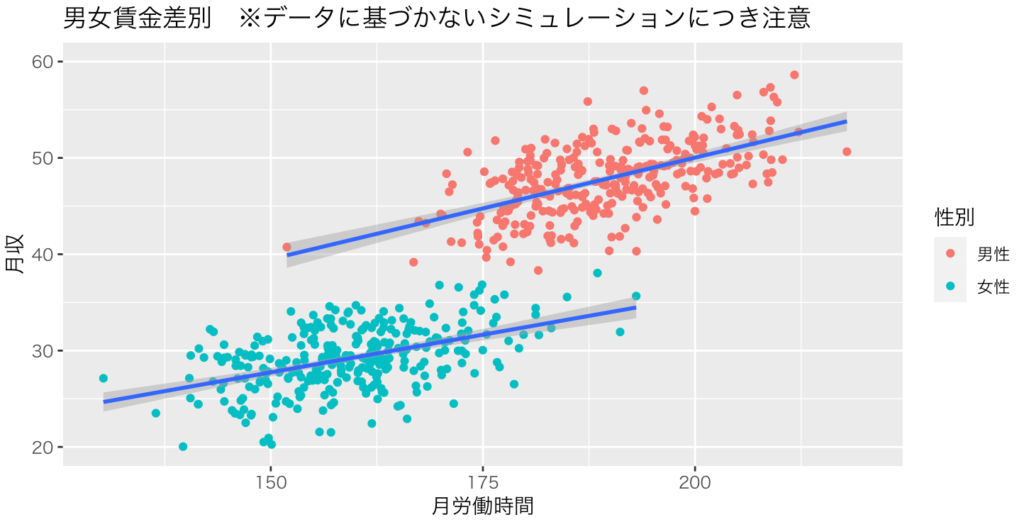
交差項の導入とは、相手の立場に立って「この人が直面している世界と、あの人が直面している世界は違うかもしれない」と慎重に考えることと言える。立場が異なれば、因果関係の構造が異なり、同じ状況を入力しても自分と異なる結果が出力されることがあり得る。例えば、女性が一生懸命に働いても、男性より稼げないかもしれない。日本人が一生懸命に働いても、月収800万円のドバイの物乞い※には勝てないかもしれない。
※Beggar caught with over Dh270,000 in Dubai(Dh270,000≒800万円)なお、ドバイのあるアラブ首長国連邦(UAE)では、2018年に物乞い防止法が施行され、物乞いが違法となった。
執筆者:しまうま総研
本文は以上。以下は付録。
問1:交差項を用いたモデリング
問1:次のような男女の賃金格差をモデル化せよ。便宜上、次の数値を用いよ。ただし、この数値は実際のデータと異なる。
・労働時間ゼロにおいて、男性は10万円/月、女性は6万円/月の所得を得る。
・男性の時給は2,000円(=0.2万円)、女性の時給は1,500円(=0.15万円)である。
・定式化は以下の通り。βは母回帰係数。月収の単位は万円。
$$月収=\beta_0+\beta_1 D_{男}+\beta_2 労働時間+\beta_3 労働時間 D_{男}+U$$
$$\beta:母回帰係数,U:誤差項$$
(解答)
基本的な発想は「たくさん働けば、たくさんお金を稼げる」であるべきであるので
$$月収=\beta_0+\beta_1 労働時間+U$$
である。しかし、
・性別によって回帰係数が異なるので、交差項が必要
・性別によって定数項が異なるので、ダミー変数が必要
である。以上を踏まえると、
$$月収=6+4 D_{男}+0.15 労働時間+0.05 労働時間D_{男}+U$$
問2:標本例のシミュレーション
問2:次のような標本例をR言語によるシミュレーションで作成せよ。

シミュレーションでは、以下のように考えた。
・サンプル・サイズは男性300、女性300の計600。
・女性は、平均して月160時間働く。(月残業0時間)
・男性は、平均して月190時間働く。(月残業時間30時間)
・母集団モデルの定式化は以下の通り。
$$月収=6+4 D_{男}+0.15 労働時間+0.05 労働時間D_{男}+U$$
(解答)
R言語のコードは記事最後に載せた。
問3:Rによる推定方法
問3:交差項のある交互作用モデルをRで推定してみよう。
(1)次の交差項のある交互作用モデルをRで推定する際のコードを答えよ。
$$推定モデル0 Y=\widehat{\beta_0}+\widehat{\beta_1} X_1 +\widehat{\beta_2} X_2 +\widehat{\beta_3} X_1 X_2+\widehat{U}$$
$$\widehat{\beta}:標本回帰係数(最小二乗推定値),\widehat{U}:残差$$
(2)男女賃金差の標本例について、推定モデル1(交互作用モデル)を用いて重回帰分析を行え。
$$母集団モデル:月収=6+4 D_{男}+0.15 労働時間+0.05 労働時間D_{男}+U$$
$$推定モデル1:月収=\widehat{\beta_0}+\widehat{\beta_1} D_{男}+\widehat{\beta_2} 労働時間+\widehat{\beta_3} 労働時間 D_{男}+\widehat{U}$$
$$\widehat{\beta}:標本回帰係数(最小二乗推定値),\widehat{U}:残差$$
(3)母集団モデルのパラメーターと、推定モデル1の推定値を比較して、考察せよ。
(解答)
(1)
推定モデル0のR言語による最小二乗推定は、次のコードで実行できる。
$$推定モデル0 Y=\widehat{\beta_0}+\widehat{\beta_1} X_1 +\widehat{\beta_2} X_2 +\widehat{\beta_3} X_1 X_2+\widehat{U}$$
lm(y ~ x1 + x2 + I(x1 * X2), data = データフレーム名)(2)
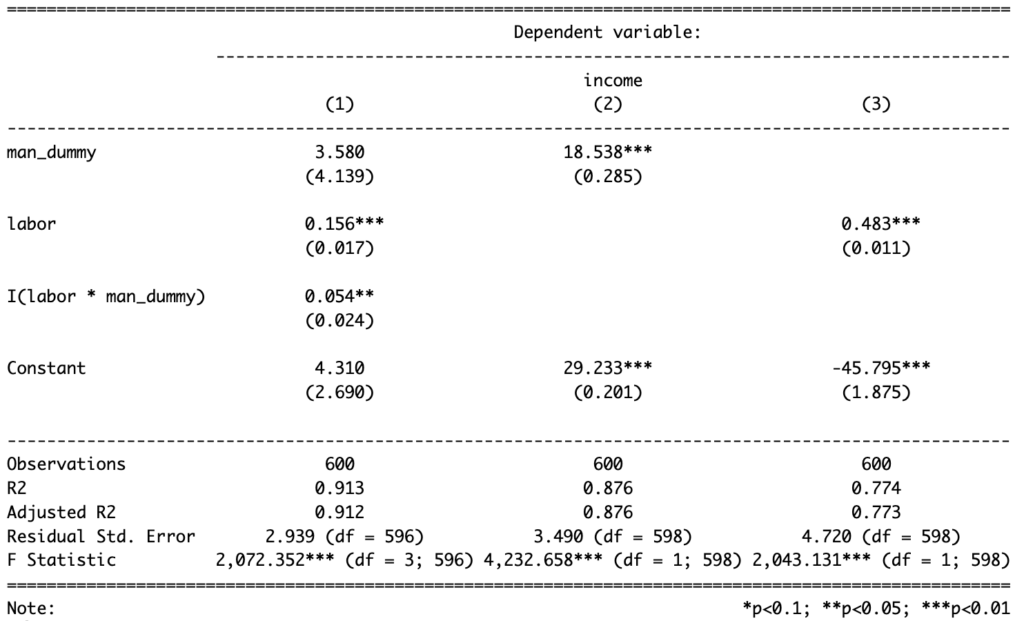
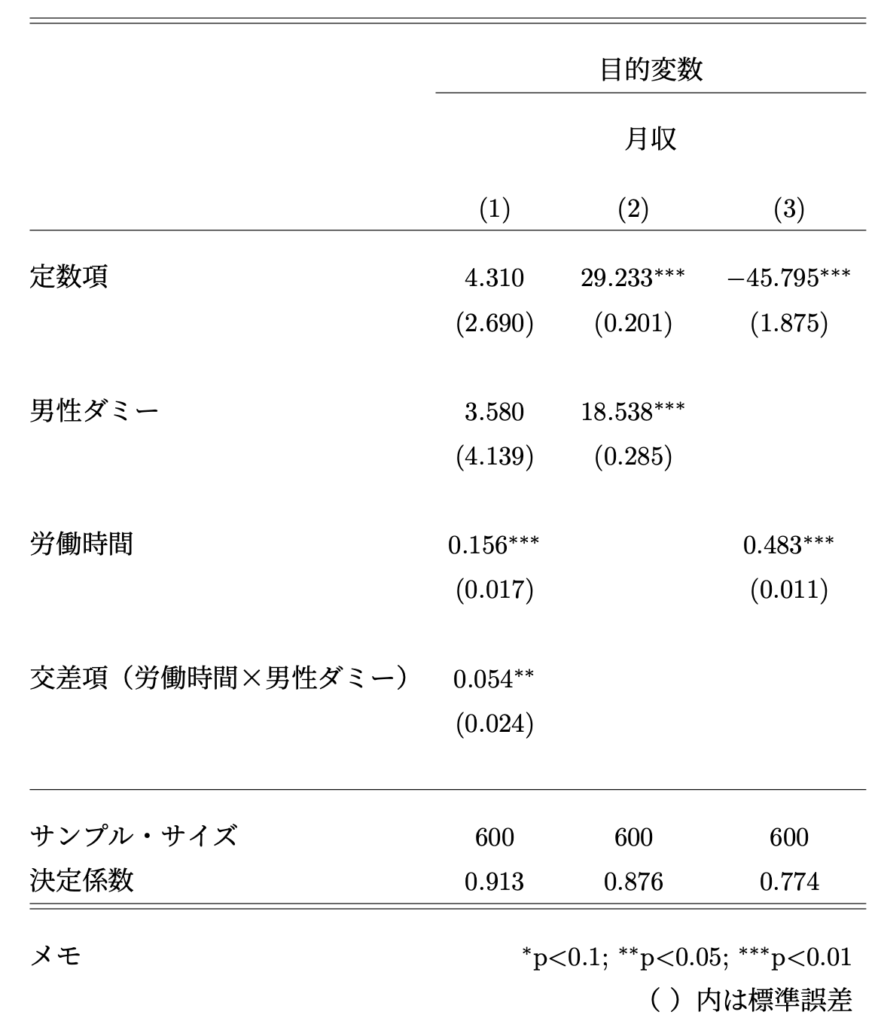
推定モデル1の推定を行った結果、次の推定結果が得られた。
$$推定モデル1:月収=4.31+3.58 D_{男}+0.156 労働時間+0.054 労働時間 D_{男}+\widehat{U}$$
(3)
推定モデル1にて、男性の時給は2,100円(=0.156万円+0.054万円)、女性の時給は1,560円(=0.156万円)と推計されている。
母集団モデルに反映させた「男性の時給は2,000円、女性の時給は1,500円」がしっかり推計されている。
$$母集団モデル:月収=6+4 D_{男}+0.15 労働時間+0.05 労働時間D_{男}+\widehat{U}$$
問4:定式化の誤り
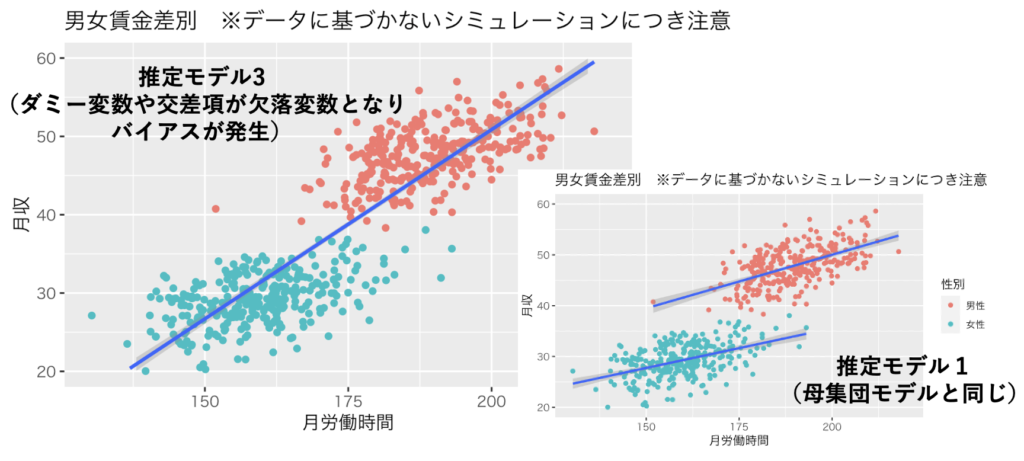
問4:母集団モデルが交互作用モデルであるのに、別のモデルで推定を行った場合、何が起こるのかを考察しよう。
$$母集団モデル:月収=6+4 D_{男}+0.15 労働時間+0.05 労働時間D_{男}+U$$
$$推定モデル1:月収=\widehat{\beta_0}+\widehat{\beta_1} D_{男}+\widehat{\beta_2} 労働時間+\widehat{\beta_3} 労働時間 D_{男}+\widehat{U}$$
$$推定モデル2:月収=\widehat{\beta_0}+\widehat{\beta_1} D_{男}+\widehat{U}$$
$$推定モデル3:月収=\widehat{\beta_0}+\widehat{\beta_2} D_{労働時間}+\widehat{U}$$
$$\widehat{\beta}:標本回帰係数(最小二乗推定値),\widehat{U}:残差$$
(1)推定モデル1、推定モデル2、推定モデル3で推定せよ。
(2)推定モデル2(男性ダミー変数のみの男女平均差モデル)の推定結果を考察せよ。
(3)推定モデル3(労働時間の単回帰モデル)の推定結果を考察せよ。
(解答)
(1)
推定した結果、以下のようになった
$$推定モデル1:月収=4.31+3.58 D_{男}+0.156 労働時間+0.054 労働時間 D_{男}+\widehat{U}$$
$$推定モデル2:月収=29.2+18.5 D_{男}+\widehat{U}$$
$$推定モデル3:月収=-45.8+0.483 D_{労働時間}+\widehat{U}$$
よくある回帰分析表にすると、次のようになった。
(2)
$$推定モデル2:月収=29.2+18.5 D_{男}+\widehat{U}$$
推定モデル2では、月収の男女差別を18.58万円と推計している。この差別は、労働時間ゼロでの差別額と、時給の差別の合算である。
母集団モデルでは
$$月収=\beta_0+\beta_1 D_{男}+\beta_2 労働時間+\beta_3 労働時間 D_{男}+U$$
$$=\beta_0+(\beta_1+ \beta_3 労働時間)D_{男}+\beta_2 労働時間+U$$
$$男女の賃金格差=\beta_1+ \beta_3 労働時間の差=4+0.5 \times 30=19万円$$
である。よって、結果論の推定としては正しいが「労働時間ゼロにおける男女の賃金格差は4万円。残りは時給500円の格差と、労働時間30時間の差によって生じる」という理解と少しずれる。「月収差の原因の一つは、労働時間の差、苦労の差」という点においては、男性の高月収は擁護される。
(3)
$$推定モデル3:月収=-45.8+0.483 D_{労働時間}+\widehat{U}$$
推定モデル3では男女の平均時給を4,830円と過大に推計している。これはダミー変数や交差項が欠落変数となり、バイアスが発生しているからである。
プログラミング・コード
#(必要な人のみ)パッケージのインストール
install.packages("ggplot2")
install.packages("stargazer")
#データの作成
sample_size <- 600 #サンプル・サイズ
man_dummy <- c(rep(c(0:1),c(rep(300,2)))) #ダミー変数
sex <- c(rep(c("woman","man"),c(rep(300,2)))) #性別
labor0 <- rnorm(n=sample_size, mean =160, sd=10) #労働時間の乱数生成
labor <- man_dummy*30+labor0 #男性の方が平均して月30時間多く働く
u <- rnorm(n=sample_size, mean =0, sd=3) #誤差項
income <- 6 + 4*man_dummy + 0.15*labor + 0.05*labor*man_dummy +u #所得
Data1 <-data.frame(labor, income,man_dummy,sex) #データフレーム化
#綺麗な散布図の描画のためのパッケージ起動
library(ggplot2)
#問2の答え
ggplot(Data1,aes(x =labor, y=income,stat = sex))+
geom_point(aes(colour=sex))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
scale_x_continuous(limits = c(130, 220))+
scale_y_continuous(limits = c(20, 60))+
labs(color = "性別")+
scale_color_hue(name = "性別", labels = c(man = "男性", woman ="女性") ) +
xlab("月労働時間") +
ylab ("月収") +
ggtitle("男女賃金差別 ※データに基づかないシミュレーションにつき注意")+
theme_grey(base_family = "HiraKakuPro-W3")
#回帰分析(推定値のみ) #問3、問4の答え
lm(income ~ man_dummy+labor + I(labor*man_dummy),data=Data1) #モデル1
lm(income ~ man_dummy,data=Data1) #モデル2
lm(income ~ labor,data=Data1) #モデル3
#回帰分析(推定結果の詳細)
reg1 <- lm(income ~ man_dummy+labor + I(labor*man_dummy),data=Data1)
reg2 <- lm(income ~ man_dummy,data=Data1)
reg3 <- lm(income ~ labor,data=Data1)
summary(reg1)
#綺麗な回帰分析表出力のためのパッケージ起動 #問4の答え
library(stargazer)
#回帰分析結果の一覧
stargazer(reg1, reg2,reg3,type="text") #問4(1)の答え
#モデル2で解釈した標本 #問4(2)
ggplot(Data1,aes(x =man_dummy, y=income))+
geom_jitter(width = 0.1,aes(colour=sex))+
scale_x_continuous(limits = c(-0.3, 1.3))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
scale_color_hue(name = "性別", labels = c(man = "男性", woman ="女性") ) +
xlab("月労働時間") +
ylab ("月収") +
ggtitle("男女賃金差別 ※データに基づかないシミュレーションにつき注意")+
theme_grey(base_family = "HiraKakuPro-W3")
#モデル3で解釈した標本 #問4(3)
ggplot(Data1,aes(x =labor, y=income))+
geom_point(aes(colour=sex))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
scale_x_continuous(limits = c(130, 220))+
scale_y_continuous(limits = c(20, 60))+
labs(color = "性別")+
scale_color_hue(name = "性別", labels = c(man = "男性", woman ="女性") ) +
xlab("月労働時間") +
ylab ("月収") +
ggtitle("男女賃金差別 ※データに基づかないシミュレーションにつき注意")+
theme_grey(base_family = "HiraKakuPro-W3")