内生性(endogeneity)とは、誤差項と説明変数が相関することを意味する。より正確には、内生性とはk種の説明変数Xで条件付けられた誤差項Uの期待値が0でないことである。
$$モデル Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k+U$$
$$内生性 E(U|X_1,X_2 \cdots X_k)≠0$$
内生性があると、重回帰分析したとき、最小二乗推定量β^は不偏性も一致性も失うことが知られている。つまり、内生性があるのならば、β1をバイアスなしに推定できず、サンプル・サイズを増やしてもバイアスは除去できない。例えば、図1が誤差項に内生性があるかないかで、散布図に引かれた回帰直線の正負が変わってしまう例である。回帰直線は単回帰分析の結果の図示だが、重回帰分析にしても内生性があると大きなバイアスが生まる。図2は、図1の内生性があるモデルで5000回データを生成し、5000回重回帰分析をして得られた標本回帰係数をヒストグラムにしたものである。真の値は+0.5であるのに 平均してー0.8という大きなバイアスが存在し不偏性がないことと、サンプル・サイズが増えても バイアスは減らず一致性がないことが見て取れる。
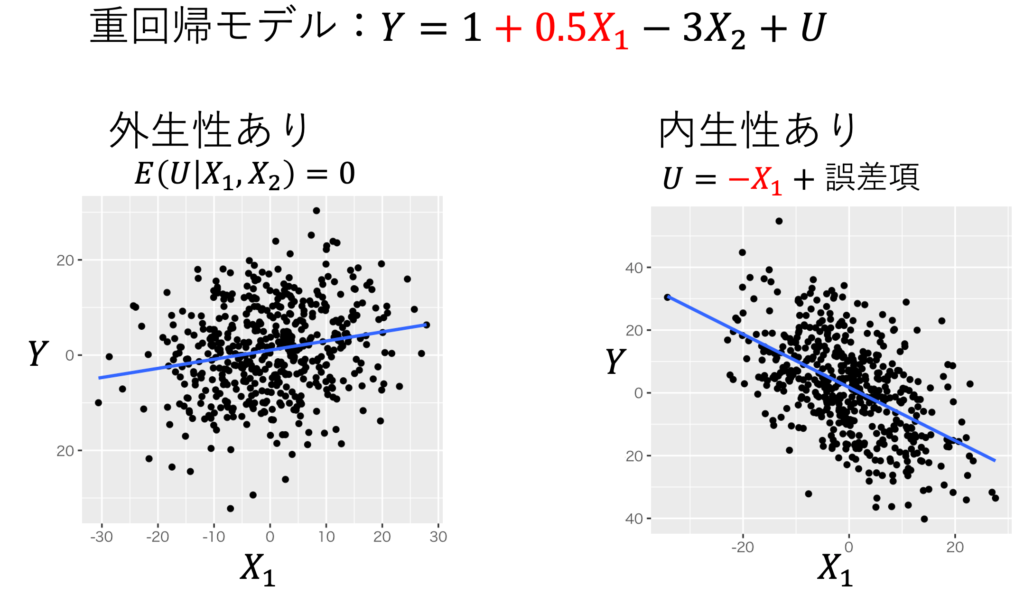
作成:しまうま
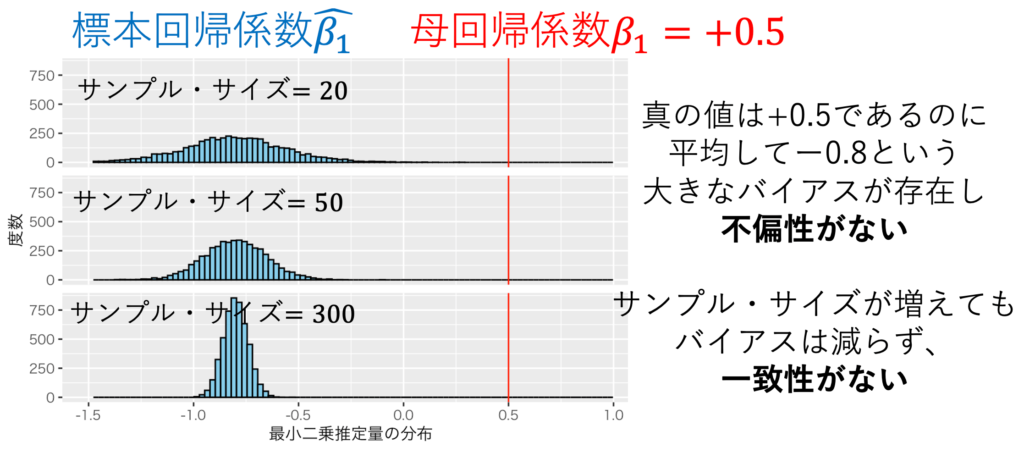
作成:しまうま
計量経済学を学ぶのは、内生性を乗り越えて、真の因果関係に迫るためでもある。内生性は観測不能な誤差項に関する現象であるため、内生性があるのかないのかすらもデータからは判断できない。それでも、社会データから意味のある示唆を引き出すために、計量経済学者たちは統計的手法を工夫してきた。
【追記】
Rコードは次の通り。
#パッケージの呼び出し
library(ggplot2)
#内生性のあるモデル
sample_size <- 500
x1_g<- rnorm(sample_size, 0,10)
x2_g<- rnorm(sample_size, 0,3)
x1_n<- rnorm(sample_size, 0,10)
x2_n<- rnorm(sample_size, 0,3)
u_gaisei <- rnorm(sample_size, 0,2)
u_naisei <- -1*x1_n + rnorm(sample_size, 0,10)
y_g <- 1 + 0.2*x1_g - 3*x2_g + u_gaisei
y_n <- 1 + 0.2*x1_n - 3*x2_n + u_naisei
data0 <- data.frame(x1_g,x2_g,u_gaisei,y_g,x1_n,x2_n,u_naisei,y_n)
#外生性のある標本を作る
ggplot(data0, aes(x = x1_g,y=y_g)) +
geom_point() +
stat_smooth(method = "lm", formula='y~x', se = FALSE)+
xlab("説明変数X") +
ylab ("目的変数Y") +
ggtitle ("サンプル・サイズ500で標本を生成した例") +
theme_grey(base_family = "HiraKakuPro-W3")
#内生性のある標本を作る
ggplot(data0, aes(x = x1_n,y=y_n)) +
geom_point() +
stat_smooth(method = "lm", formula='y~x', se = FALSE)+
xlab("説明変数X") +
ylab ("目的変数Y") +
ggtitle ("サンプル・サイズ500で標本を生成した例") +
theme_grey(base_family = "HiraKakuPro-W3")
#最小二乗推定量の分布を生成する
trial_number <- 5000 #試行回数
beta_1_size1 <- rep(NA, trial_number)
beta_1_size2 <- rep(NA, trial_number)
beta_1_size3 <- rep(NA, trial_number)
#n=20、5000回標本生成と回帰分析を繰り返す
sample_size1 <- 20
for(j in 1:trial_number){
x1_n <- rnorm(sample_size1, 0,10)
x2_n <- rnorm(sample_size1, 0,3)
u_naisei <- -1*x1_n + rnorm(sample_size1, 0,10)
y_n <- 1 + 0.2*x1_n - 3*x2_n + u_naisei
answer <- lm(y_n ~ x1_n + x2_n)
beta_1_size1[j] <- summary(answer)$coef["x1_n","Estimate"]
}
#n=50、5000回標本生成と回帰分析を繰り返す
sample_size2 <- 50
for(j in 1:trial_number){
x1_n<- rnorm(sample_size2, 0,10)
x2_n<- rnorm(sample_size2, 0,3)
u_naisei <- -1*x1_n + rnorm(sample_size2, 0,10)
y_n <- 1 + 0.2*x1_n - 3*x2_n + u_naisei
answer <- lm(y_n ~ x1_n + x2_n)
beta_1_size2[j] <- summary(answer)$coef["x1_n","Estimate"]
}
#n=300、5000回標本生成と回帰分析を繰り返す
sample_size3 <- 300
for(j in 1:trial_number){
x1_n<- rnorm(sample_size3, 0,10)
x2_n<- rnorm(sample_size3, 0,3)
u_naisei <- -1*x1_n + rnorm(sample_size3, 0,10)
y_n <- 1 + 0.2*x1_n - 3*x2_n + u_naisei
answer <- lm(y_n ~ x1_n + x2_n)
beta_1_size3[j] <- summary(answer)$coef["x1_n","Estimate"]
}
#推定量の分布の描画
library(tidyverse)
tibble(size020=beta_1_size1, size050=beta_1_size2, size300=beta_1_size3)%>%
gather(key=n,value=value,size020,size050,size300)%>%
ggplot() +
geom_histogram(aes(x = value),bins=100,fill="skyblue", color= "black") +
geom_vline(xintercept = 0.5, color = "red") +
scale_x_continuous(limits = c(-1.5, 1)) +
facet_grid(n~.)+
xlab("最小二乗推定量の分布") +
ylab ("度数") +
theme_grey(base_family = "HiraKakuPro-W3")