固定効果モデル(fixed effects model)とは「個体ごとに異なり」「時間を通じて一定」な固定効果を、重回帰モデルに加えたモデルだ。固定効果が観測できず、欠落変数になっている場合に使われる。パラメーターの推定には固定効果法が使われる。モデルは下の式の通りである。iは個体番号、tは時間、kは説明変数の数を意味する。
$$固定効果モデル Y_{it}=\beta_{0}+ \alpha_i+\beta_1 X_{1it} +\cdots + \beta_kX_{kit}+U_{it}$$
$$固定効果=固定効果の平均\beta_{0}+ 個体ごとの乖離差\alpha_i$$
$$i:個体番号、t:時間、k:説明変数の数$$
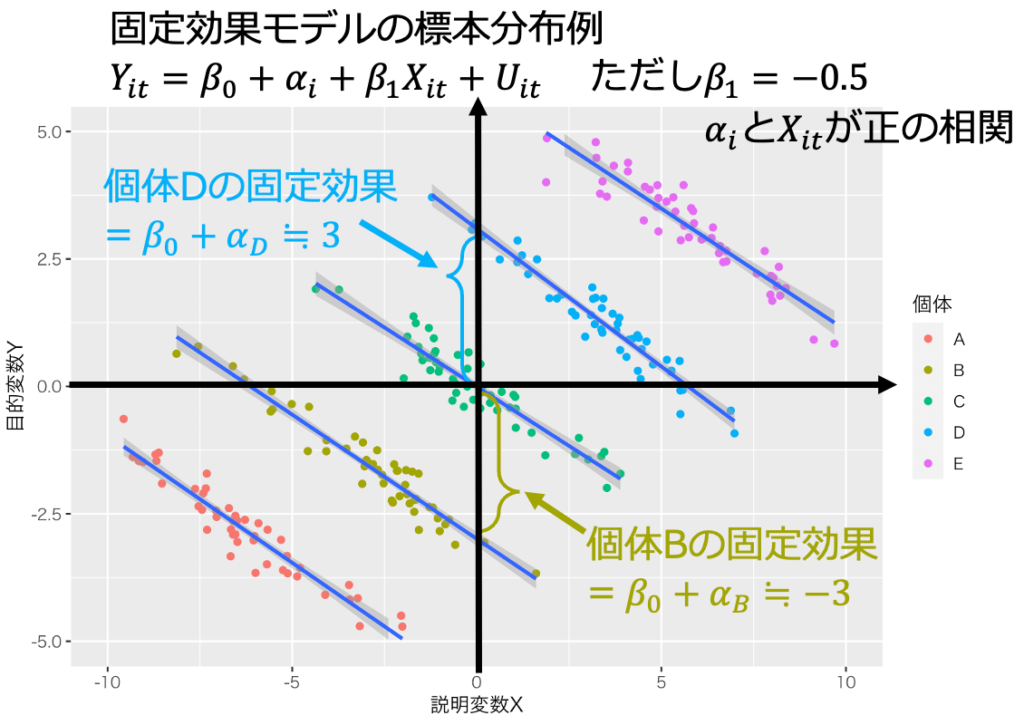
固定効果モデルを重回帰モデルと解釈すると不適切な場合がある。固定効果が他の説明変数Xと相関する場合、内生性が発生し、最小二乗推定量はバイアスをもつ。図1と図2は、固定効果が他の説明変数Xと相関し、最小二乗推定量がバイアスをもつ場合である。
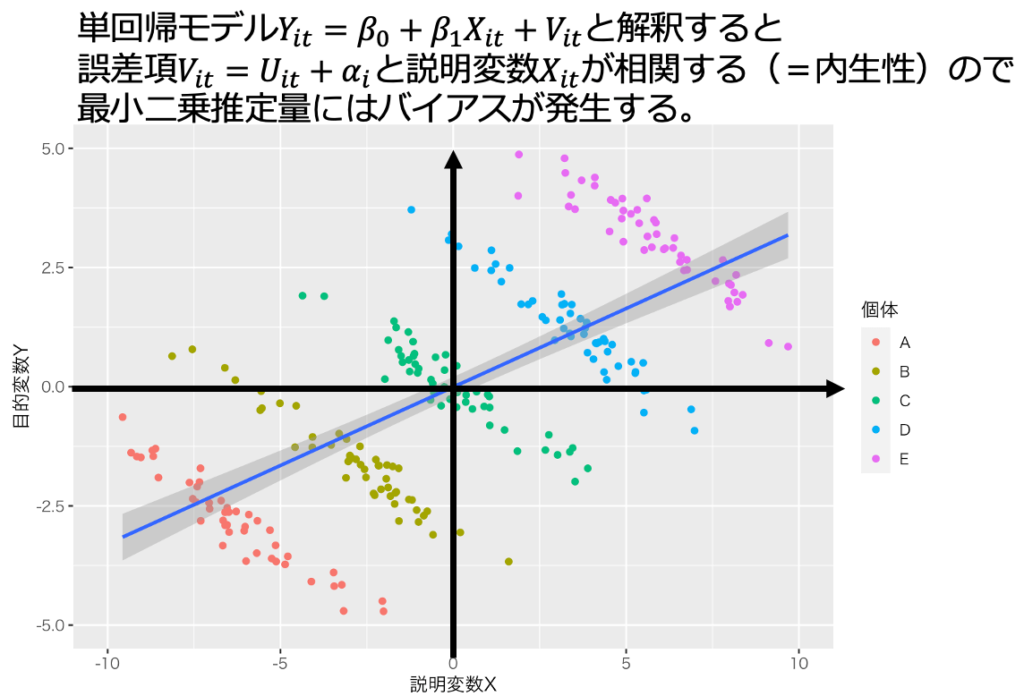
固定効果モデルを用いた「固定効果法・固定効果推定量」を用いると、一部の内生性の問題に対処できる。固定効果法で対処できる内生性とは「観測できず、説明変数Xと相関するが、個体内では時間と通じて一定の欠落変数(=固定効果)がもたらす内生性」である。
本文は以上。以下は付録。
執筆の目的
固定効果モデルは、パネルデータ分析で人気の固定効果法を理解するのに役立つので、執筆した。
また、固定効果モデルは「個体によって定数項が異なる(=個人差がある)」を考慮せずに現象を解釈すると、重大な誤りが発生しうることを示唆するので、面白い。
問1:固定効果推定量
母集団モデルとしての固定効果モデルを理解した後は、どんな方法で推定するかが実際的な問題になる。
問1:固定効果モデルではどんな推定量が使われるか。
固定効果モデルでは、固定効果法という手法をよく用いる。固定効果法を用いて得られる推定量を、固定効果推定量と呼ぶ。詳しくは「固定効果推定量について / パネルデータ分析による内生性への対応」をご覧いただきたい。
問2:固定効果モデルの仮定
統計モデルとして固定効果モデルを用いるならば、どんな仮定が課せられているのかを知る必要がある。
問2:固定効果モデルの仮定は何か。
固定効果モデルは、固定効果推定量が不偏性、一致性、漸近正規性をもつために、次の4つの仮定を満たす。
仮定1:モデルの定式化に誤りがない。
$$固定効果モデル Y_{it}=\beta_{0}+ \alpha_i+\beta_1 X_{1it} +\cdots + \beta_kX_{kit}+U_{it}$$
$$固定効果=固定効果の平均\beta_{0}+ 個体ごとの乖離差\alpha_i$$
$$i:個体番号、t:時間、k:説明変数の数$$
仮定2:標本が無作為抽出されている。
仮定3:完全な共線関係がない。
仮定4:強外生性がある。
強外生性とは
$$E \left( U_{it} \Big| \alpha_i, \{X_{1it} ,X_{2it} \cdots X_{kit} \}_{t=初期}^{終期} \right)=0$$
という条件である。つまり、
・個体iのt期の誤差項は、個体iにおけるすべての期の説明変数X1〜Xkと相関してならない。(強外生性)
という条件である。補足しておくと、通常の外生性は
$$E(U_{it}|\alpha_i, X_{1it} ,X_{2it} \cdots X_{kit})=0$$
・個体iのt期の誤差項は、個体iにおけるt期の説明変数X1〜Xkと相関してならない。
である。
問3:モデリングの例
固定効果モデルの数理的な特徴がわかったが、実際にはどんなモデルが考えられるのだろうか。
問3:どんな固定効果モデルを用いたモデリング例が考えられるか。
固定効果モデルとは、時間一定の個体差である固定効果を取り除くモデルである。さらに、固定効果モデルを使うときは、観測できない場合である。なぜなら、固定効果が観測できるならば、それを説明変数Xとして加えれば良いからである。
$$固定効果モデル Y_{it}=\beta_{0}+ \alpha_i+\beta_1 X_{1it} +\cdots + \beta_kX_{kit}+U_{it}$$
注意すべき点が一つある。それは「時間一定の要因」を説明変数Xとすることはできないという点だ。なぜなら、それは固定効果に含まれてしまうからである。
例えば、こんなモデルが考えられる。
・目的変数Y_it=iさんのt年におけるTOEICのスコア
・説明変数X_it=iさんのt年における英文法学習時間
・固定効果=もともとの英語力(帰国子女 or 純ジャパなど)
$$(TOEICのスコア)_{it}=\beta_{0}+ (もともとの英語力)_i+\beta_1 (英文法学習時間)_{it} +U_{it}$$
もし「もともとの英語力が高いと、英文法をあまり勉強しない」という関係があるならば、固定効果と説明変数は相関する。この場合、重回帰モデルでモデリングすると、内生性バイアスが発生する。具体的には
$$(TOEICのスコア)_{it}=\beta_{0}+\beta_1 (英文法学習時間)_{it} +\Big[ U_{it} + (もともとの英語力)_i \Big]$$
において
$$(英文法学習時間)_{it} と \Big[ U_{it} + (もともとの英語力)_i \Big]が負の相関する$$
ので「英文法を勉強しない方がTOEICの点数が高くなる」という結果がでうる。
問4:回帰係数
母集団モデルに立ち戻って、そもそも固定効果モデルの回帰係数の意味合いは何かについて考察したい。
問4:因果推論の文脈では、母回帰係数はどのように解釈できるか。
回帰係数が平均処置効果になる。例えば
$$Y_{it}=\beta_0+\alpha_i -0.5 X_{it}+U_{it}$$
という固定効果モデルの場合、ある個体のXを1増やす施策を実施すると、その個体のYが平均してマイナス0.5される。

問5:バイアス
本文では固定効果モデルに最小二乗法を適用して「バイアスが発生する」と述べたが、そもそもバイアスが発生するとどんな問題があるのか。
問5:バイアスが発生すると意思決定においてどんな問題が起きうるのか。
バイアスを回避しないと、誤った因果関係を根拠にした意思決定を導いてしまう可能性があるのが問題だ。
例えば、画像1や画像2の場合を考えよう。「Xが大きいとYが大きい」という相関関係があるので、素直に観測結果を解釈すると「Xを増やすとYが増える」という因果関係を導いてしまう。しかし、これは実際の因果効果の真逆である。この誤った因果関係を根拠に政策を立案すれば、意図した結果が得られない。

問6:固定効果モデルのシミュレーション
本文で掲載した画像の生成方法が気になる人向けに、プログラミングについても付記しておいた。
問6:本文の画像1、画像2のようなシミュレーションはどのように実行したのか。
画像1と画像2はR言語を用いたモンテカルロ・シミュレーションによって作成した。具体的なコードは以下の通り。
#(必要な人のみ)パッケージのインストール
install.packages("plm") #散布図描画
install.packages("ggplot2") #パネルデータ分析
##5組50期間のパネルデータの生成
sample_size <- 250
Group_number <- c(rep(c(1:5),c(rep(50,5))))
Personal_number <- c(rep(1:50,5))
Category <- c(rep(c("A","B","C","D","E"),c(rep(50,5))))
fixed_effect <- (Group_number-3)*3 #固定効果
ramdom<- rnorm(n=sample_size, mean =0, sd=2)
X <- ramdom + fixed_effect
u <- rnorm(n=sample_size, mean =0, sd=0.3)
Y <- fixed_effect-0.5*X+u
cor(X,fixed_effect) #説明変数Xと固定効果の相関係数
Data1 <-data.frame(X, Y,fixed_effect,Group_number,Personal_number,Category)
#綺麗な散布図の描画のためのパッケージ起動
library(ggplot2)
#画像1
ggplot(Data1,aes(x =X, y=Y,stat = Category))+
geom_point(aes(colour=Category))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
scale_x_continuous(limits = c(-10, 10))+
scale_y_continuous(limits = c(-5, 5))+
labs(color = "個体")+
xlab("説明変数X") +
ylab ("目的変数Y") +
theme_grey(base_family = "HiraKakuPro-W3")
#画像2
ggplot(Data1,aes(x =X, y=Y))+
geom_point(aes(colour=Category))+
stat_smooth(method = "lm", formula='y~x', se = TRUE)+
scale_x_continuous(limits = c(-10, 10))+
scale_y_continuous(limits = c(-5, 5))+
labs(color = "個体")+
xlab("説明変数X") +
ylab ("目的変数Y") +
theme_grey(base_family = "HiraKakuPro-W3")
#パネルデータ分析用のパッケージを起動
library(plm)
#plm用のデータに変換
Data2 <- pdata.frame(Data1, index = c("Group_number","Personal_number"))
#最小二乗法を実行
model_OLS <- plm(formula = Y ~X,model="pooling",data=Data2)
summary(model_OLS)
#固定効果法を実行
model_FE <- plm(formula = Y ~X,model="within",data=Data2)
summary(model_FE)