操作変数モデル(instrumental viables model)は、誤差項Uと「内生変数の説明変数X」が相関する内生性をもつ重回帰モデルで、操作変数Zが存在するモデルである。なお、誤差項Uと「外生変数の説明変数W」は相関しない。そして、操作変数Zとは、誤差項Uとは相関しない(外生性)が、内生変数の説明変数Xとは相関する(関連性)ような変数である。操作変数モデルの場合、操作変数法という推定方法が操作変数使えることが知られている。そして、操作変数の数mは、内生変数の数k以上である必要がある(次数条件)。
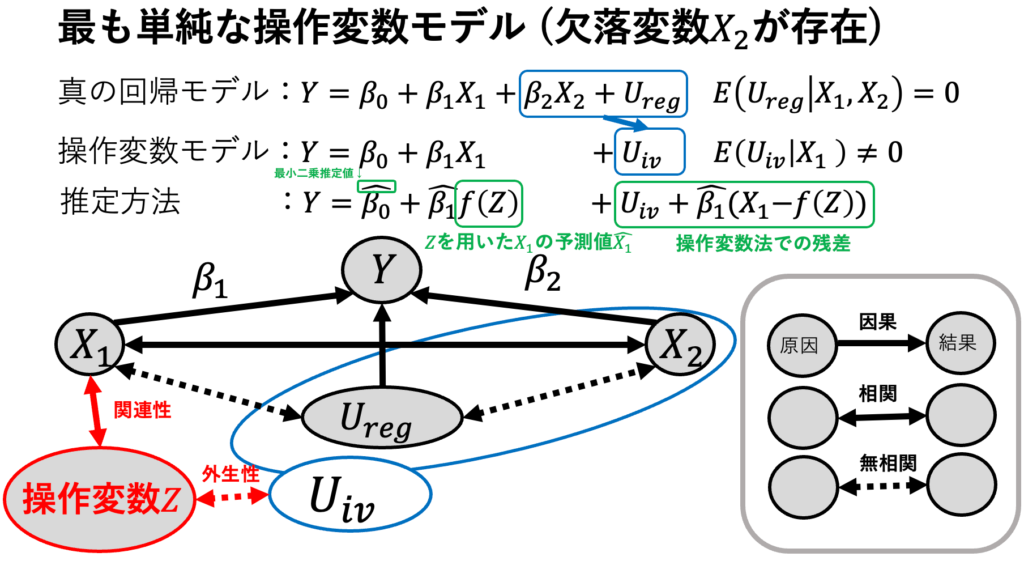
$$操作変数モデル Y=\beta_0 +\beta_1 X_1 + \cdots + \beta_k X_k$$
$$+\beta_{k+1} W_{k+1} + \cdots + \beta_{k+p} W_{k+p}+U$$
$$説明変数の内生性 E(U|X_1,X_2 \cdots X_k)≠0$$
$$外生性と関連性のある操作変数Z_1, \cdots ,Z_mが存在する$$
操作変数モデルをシミュレーションしてみよう。式①は、単回帰モデルだ。しかし、式②と式③にある欠落変数X2によって、説明変数X1と誤差項Uが相関し、内生性が生まれている。一方で、式②と式③より、操作変数Zは説明変数X1には影響を与える(関連性)が、誤差項Uには影響を与えない(外生性)。このモデルにしたがって、ランダムに標本を生成した。β1のパラメーターはプラスなのに、見かけ上はマイナスという強い内生性バイアスがかかっている。最小二乗法(OLS)で推定すると「-4.7」になった。しかし、操作変数法(IV)である2段階最小二乗法(2SLS)で推定すると「+1.96」となり、真の値である「+2」に近い推定ができた。
$$式①:Y=30+2X_1+U$$
$$式②:X_1=10 + X_2 +Z +U_1、式③:U=-10X_2+U_2$$
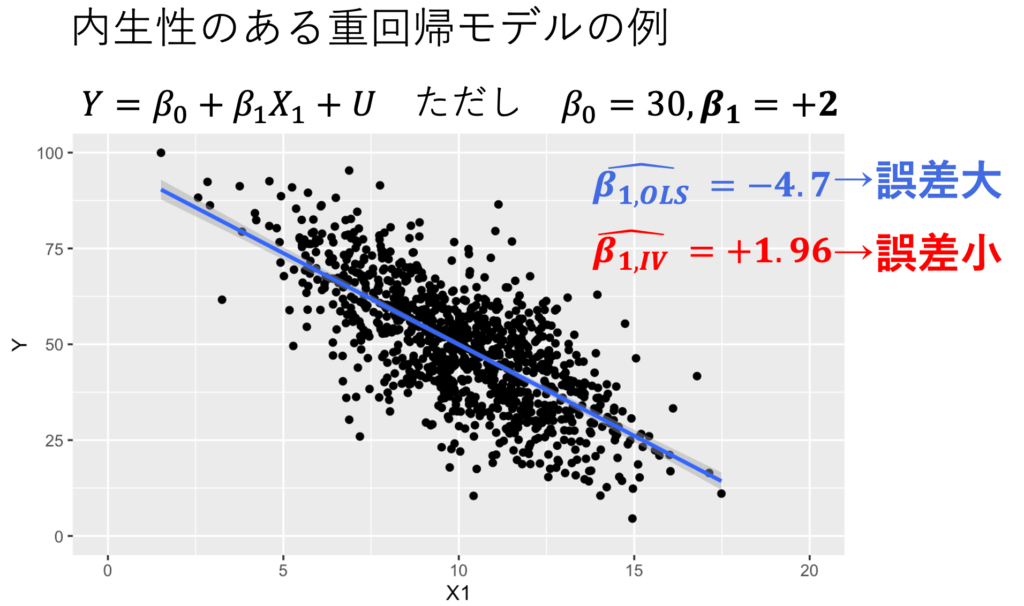
出典:しまうま総研(2023)が作成
補足:Rコードは追記に載せた。
操作変数があるのであれば、操作変数法を使いたい。操作変数推定量(IV)を用いることで、一致性、漸近正規性をもつ推定が可能になる。問題は、使いやすい操作変数がないことである。
【追記】
作図に用いたRコードはこちら。
#使うパッケージ
library(ggplot2)
library(AER)
#標本生成
sample_size <- 1000
X2 <- rnorm(sample_size, mean =0 , sd =2)
u1 <- rnorm(sample_size, mean =0 , sd =1)
u2 <- rnorm(sample_size, mean =0 , sd =1)
Z <- rnorm(sample_size, mean =0 , sd =1)
X1 <- 10 + X2 + Z + u1
U <- -10*X2 +u2
Y <- 30 + 2*X1 + U
plot(X1,Y)
Data <- data.frame(X1,Y,Z)
#図1
library(ggplot2)
ggplot(Data, aes(x = X1,y=Y))+
geom_point()+
scale_x_continuous(limits = c(0, 20))+
scale_y_continuous(limits = c(0, 100))+
geom_smooth(method ="lm")
#推定
lm(Y ~ X1, data= Data) #OLS
library(AER)
IV_reg <- ivreg(data = Data, Y ~ X1 | Z) #IV
summary(IV_reg)