プロビット・モデル(logistic regression model)は、潜在変数で解釈する際、誤差項が標準正規分布に従い、入力は重回帰モデルと同じ線形なモデルだが、出力が0か1という統計モデルである。潜在変数Y*≦0のときY=0、潜在変数Y*>0のときY=1を出力する。
$$目的変数Y=\begin{cases} 0 (Y^*≦0) \\ 1 (Y^*>0) \end{cases}$$
$$潜在変数 Y^*=\beta_0 + \beta_1 X_1 +\cdots +\beta_k X_k +U$$
$$U|X_1,X_2 \cdots X_k が標準正規分布に従う$$
プロビット・モデルは誤差項が正規分布であるが、ここをロジスティック分布に変えるとロジスティック回帰モデル、ここを一様分布に変えると線形確率モデル(重回帰モデル)となる。実のところ、この3モデルを使っても、平均限界効果については似たような結果が出る。平均限界効果とは、説明変数Xが1増えると、目的変数Yを増やす平均的な効果である。実際に、乱数発生させて作った次の標本について、3モデルで推定すると、平均限界効果はほぼ同じだ。
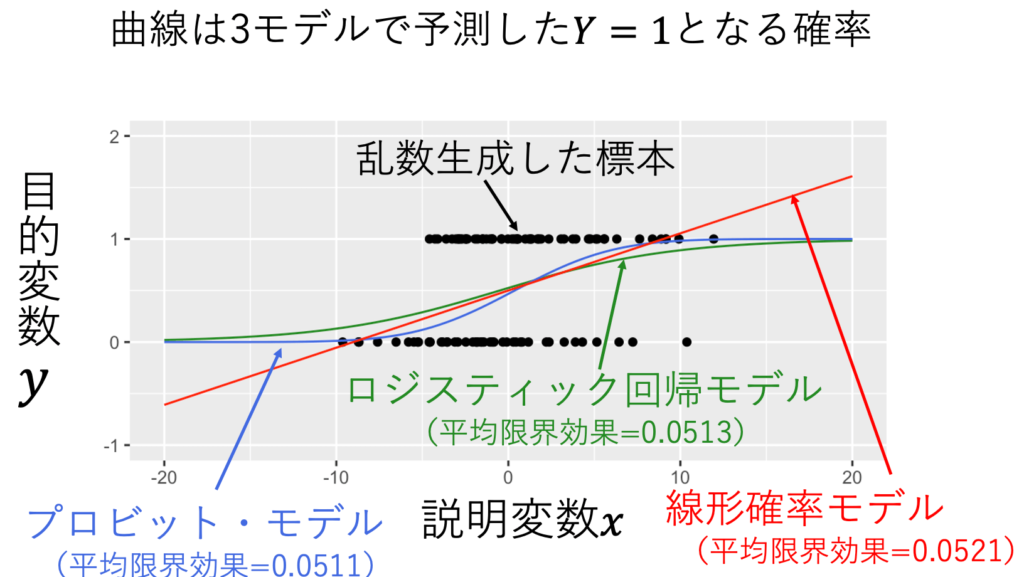
プロビット・モデルは誤差項が正規分布であるので、ロジスティック回帰モデルよりは納得感がある。しかし、平均限界効果の推定で、ロジスティック回帰モデルとほぼ同じ結果なら、どちらを使ってもいい。もっといえば、平均限界効果の推定で、線形確率モデルとほぼ同じなら、線形確率モデルの方がいいかもしれない。線形確率モデルとは重回帰モデルであり、内生性に対処できる操作変数法や固定効果法が使える。線形確率モデルには誤差項が不均一分散するという欠点はあるが、それは不均一分散に頑健な標準誤差で対応すれば問題ない。
【追記】
プロビット・モデル、ロジスティック回帰モデル、線形確率モデルを用いた推定は、Rでは次のコードで実行できる。
glm(y ~ x1 + x2 ,data=Data, family=binomial(link=probit)) #プロビット・モデル
glm(y ~ x1 + x2 ,data=Data, family=binomial(link=logit)) #ロジスティック回帰モデル
lm(y ~ x1 + x2 ,data=Data) #線形確率モデル(不均一分散に頑健な標準誤差に未対応)
library(estimatr) #呼び出し
lm_robust(y ~ x1 + x2, se_type = "stata") #線形確率モデル(不均一分散に頑健な標準誤差に対応)平均限界効果は、mfxのパッケージを利用して推定できる。
library(mfx) #呼び出し
logitmfx(y~x1+x2, data=Data) #ロジスティック回帰での平均限界効果
probitmfx(y~x1+x2, data=Data) #プロビットでの平均限界効果描画は次のRコードで実行できる。
#ggplot2の呼び出し
library(ggplot2)
#潜在変数モデルでの標本生成
sample_size <- 100
x <- rnorm(n=sample_size, mean =-0.5, sd=5)
u <- rnorm(sample_size)
yy <- 0.1 + 0.2*x+ u #潜在変数yyを作る
y <- ifelse(yy>=0,1,0) # 0を以上なら1、未満なら0の二値変数yを作る
Data <- data.frame(x,y,yy)
#分析
model_liner <- lm(y ~ x, data=Data)
model_logit <- glm(y ~ x ,data=Data,family=binomial(link=logit))
model_probit <- glm(y ~ x ,data=Data,family=binomial(link=probit))
#モデル
p_logistic <- function(x) (1/(1+(exp(1)^(-summary(model_logit)$coef["(Intercept)","Estimate"]-summary(model_logit)$coef["x","Estimate"]*x)))
p_norm <- function(x) pnorm(summary(model_probit)$coef["(Intercept)","Estimate"]+summary(model_probit)$coef["x","Estimate"]*x, mean=0, sd=1)
p_liner <- function(x) (summary(model_liner)$coef["(Intercept)","Estimate"]+summary(model_liner)$coef["x","Estimate"]*x)
#図1の描画
ggplot(Data,aes(x =x, y=y))+
geom_point()+
stat_function(fun=p_logistic , color="ForestGreen")+
stat_function(fun=p_norm, color="RoyalBlue")+
stat_function(fun=p_liner, color="Red")+
scale_x_continuous(limits = c(-20, 20))+
scale_y_continuous(limits = c(-1, 2))
#平均限界効果の計算
library(mfx)
logitmfx(y~x, data=Data) #ロジスティック回帰での平均限界効果
probitmfx(y~x, data=Data) #プロビットでの平均限界効果
#回帰分析結果の出力
library(stargazer)
stargazer(model_liner,model_logit,model_probit, type="text")