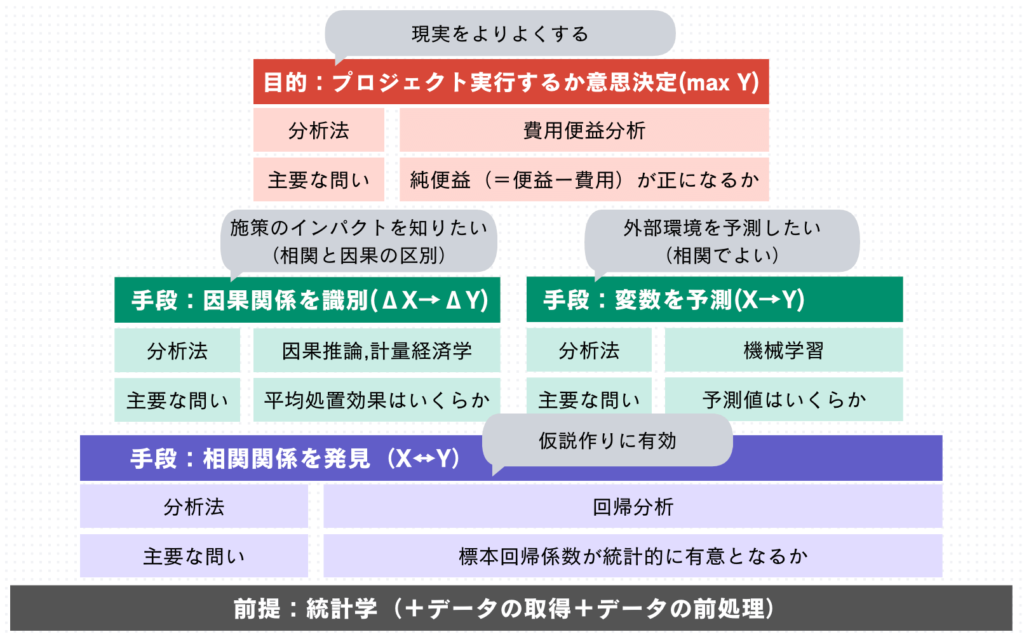
データ分析は意思決定の役に立ちます。意思決定では、純便益(=便益ー費用)がプラスになるか否かが、究極的な問いになります。この問いに答えるために、費用便益分析と計量経済学が役立ちます。
第1章:費用便益分析
・準備中
第2章:シミュレーション
・準備中
第3章:統計学
第1節:モデル
第2節:パラメーター
第3節:推定量
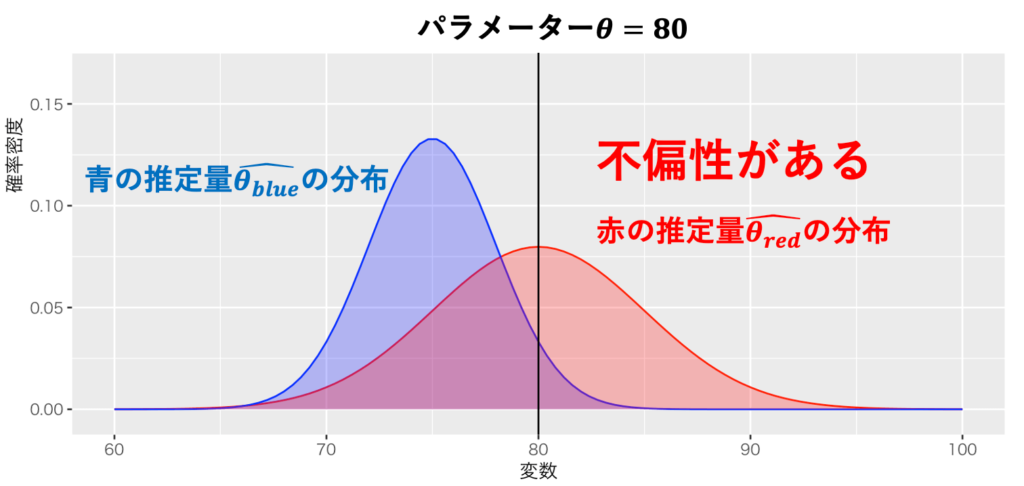
・【推定】不偏性について / 推定量の性質
・【推定】一致性について / 推定量の性質
・【推定】頑健性について / 推定量の性質
・【推定】効率性について / 推定量の性質
・【検定】仮説検定について
・【検定】標準誤差について / 仮説検定
・【検定】p値について / 仮説検定
第4章:平均分析
第1節:モデル
平均モデルでは、目的変数Yは次の式で決定される。Eは期待値、Uは誤差項を意味する。目的変数には、政策介入が行われた処置群のものと、政策介入が行われなかった対照群の目的変数のものがある。
$$Y_{処置群}=E(Y_{処置群})+U_{処置群}$$
$$Y_{対照群}=E(Y_{対照群})+U_{対照群}$$
$$なお、期待値E(Y)は定数、目的変数Yと誤差項Uは確率変数である。$$
【仮定】無作為抽出されている。サンプル・セレクション・バイアスがない。
第2節:パラメーター
・【因果推論】処置群と対照群の期待値の差βが平均処置効果。
$$パラメーター\beta=E(Y_{処置群})-E(Y_{対照群})$$
第3節:推定量
・【推定量】平均差
$$推定量 \widehat{\beta}= \overline{Y_{処置群}}- \overline{Y_{対照群}}$$
ただし、Yの平均は上に棒をつけて表すこととする。
$$Yの平均=\overline{Y}=\frac{Y_1+Y_2+ \cdots +Y_N}{N}=\frac{1}{N} \sum_{i=1}^N Y_i $$
$$i:データ番号、N:サンプル・サイズ$$
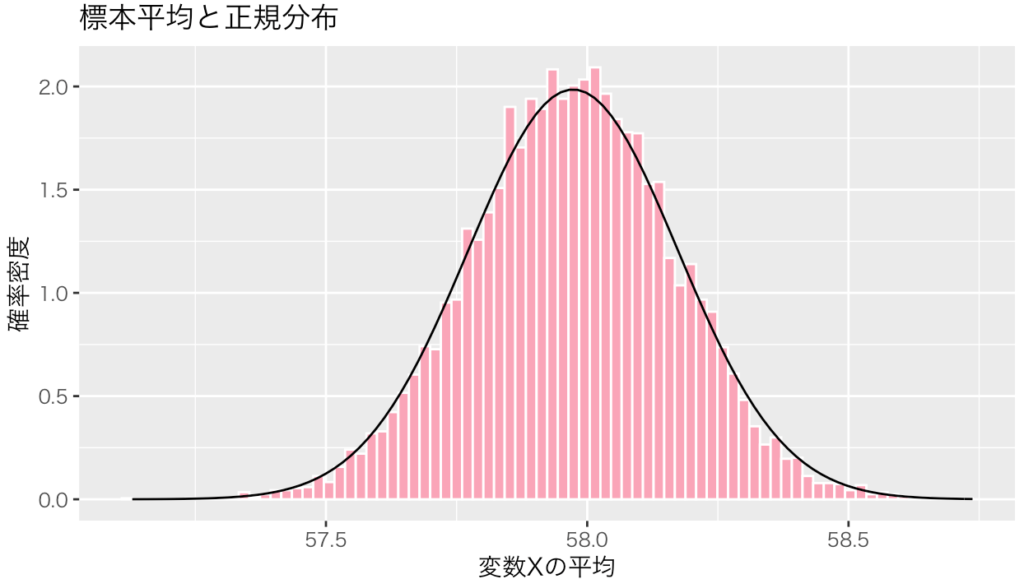
・【推定量の性質】中心極限定理について / 平均
第4節:実践
βが統計的に有意かつプラスであるならば「政策によって目的変数Yが増加する因果関係がある」と評価できる。
ただし「無作為抽出である」という仮定が満たされている必要がある。ランダム化比較試験(RCT)はそのための研究デザインである。
#平均の推定
mean(データフレーム名$変数名)
#ウェルチのt検定
t.test(x=データフレーム名$変数名A,y=データフレーム名$変数名B,var.equal=F,paired=F)第5章:重回帰分析
第1節:モデル
・【概要】重回帰モデルについて / 統計モデル
$$Y=\beta_0 +\beta_1 X_1+\beta_2 X_2 +\cdots \beta_k X_k+U$$

・【仮定1】正しい定式化がなされている。
・【仮定2】サンプリングが無作為抽出されている。
・【仮定3】完全な共線関係ではない。
・【仮定4】外生性について / 回帰モデル
・【仮定5】誤差項が自己相関していない。
・【仮定6】誤差項が均一分散している。
・【仮定7】誤差項が正規分布している。
・【仮定3の軽微な違反】多重共線性(マルチコ)について / 重回帰分析
・【仮定4の違反】内生性について / 回帰モデル

第2節:パラメーター
・【因果推論的な解釈】X1が説明変数なら、β1が平均処置効果。
第3節:推定量
・【推定量】最小二乗法(OLS)について / 推定
・【推定量】重回帰分析における最小二乗法について / 回帰分析
・【推定量の解釈】重回帰分析の解釈「削ぎ落とし(partialling out)」について / FWL定理
・【推定量の性質】最小二乗推定量の不偏性・一致性・漸近正規性について / 重回帰分析
・【標準誤差】重回帰分析の標準誤差について / 最小二乗法
第4節:実践
#Rコード
#コード1:重回帰分析(簡易版)
lm(y ~ x1 + x2, data = データフレーム名)
#コード2:重回帰分析(詳細版)
推定式名 <- lm(y ~ x1 + x2, data = データフレーム名)
summary(推定式名)
#コード3:重回帰分析(不均一分散に頑健な標準誤差に対応)
library(estimatr)
lm_robust(y ~ x1 + x2, data = データフレーム名, se_type = "stata")
β1が統計的に有意かつプラスであるならば「政策によって目的変数Yが増加する因果関係がある」と評価できる。
$$Y=\beta_0 +\beta_1 D+\beta_2 X_2 +\cdots \beta_k X_k+U$$
$$政策ありならD=1、政策なしならD=0$$
ただし「サンプリングが無作為抽出であること(仮定2)」、「外生性があること(仮定4)」が成り立たないといけない。
第6章:重回帰モデルの応用
第1節:モデル
第2節:パラメーター
・【因果推論的な解釈】βが平均処置効果。
第3節:推定量
・重回帰分析と同じ
第4節:実践
#Rコード
#コード1:ログ=レベル・モデル
lm(log(y) ~ x1 + x2, data = データフレーム名)
#コード2:ダミー変数d(すでに0,1になっているなら、そのまま入れるだけ)
lm(y ~ x + d, data = データフレーム名)
#コード3:交差項の導入
lm(y ~ x1 + x2 + I(x1*x2), data = データフレーム名)第7章:ロジスティック回帰分析
第1節:モデル
・【基本】ロジスティック回帰モデルについて / 二値選択モデル
・【応用】多項ロジスティック回帰モデルについて / 多値選択モデル(モデル:好きな教科などの説明に使えるモデル)
・【応用】順序ロジスティック回帰モデルについて / 順序選択モデル(モデル:1,2,3,4の顧客満足度などの説明に使えるモデル)
・【応用】プロビット・モデルについて / 二値選択モデル(モデル:潜在変数モデルでの誤差項が正規分布の二値選択モデル)
第2節:パラメーター
・【因果推論的な解釈】βではなく平均限界効果が平均処置効果。
第3節:推定量
・【推定量】最尤法について / 推定
・【推定量の性質】漸近正規性をもつ。
第4節:実践
#Rコード
#コード1:プロビット・モデル
PROBIT <- glm(y ~ x1 + x2 ,data=データフレーム名, family=binomial(link=probit))
summary(PROBIT)
#コード2:ロジスティック回帰モデル
LOGIT <- glm(y ~ x1 + x2 ,data=Data, family=binomial(link=logit))
summary(LOGIT)
#コード3:線形確率モデル(←不均一分散になることが知られているので、不均一分散に頑健な標準誤差を用いる)
library(estimatr)
LM <- lm_robust(y ~ x1 + x2, data = データフレーム名, se_type = "stata")
summary(LM)第8章:差の差分析
第1節:モデル
・【全体像】差の差(DID)分析について / パネルデータで因果推論
$$Y=\beta_0+\beta_1 (D_{処置群})$$
$$+\beta_2 (D_{介入後})+\beta_3 (D_{介入後})(D_{処置群})+U$$
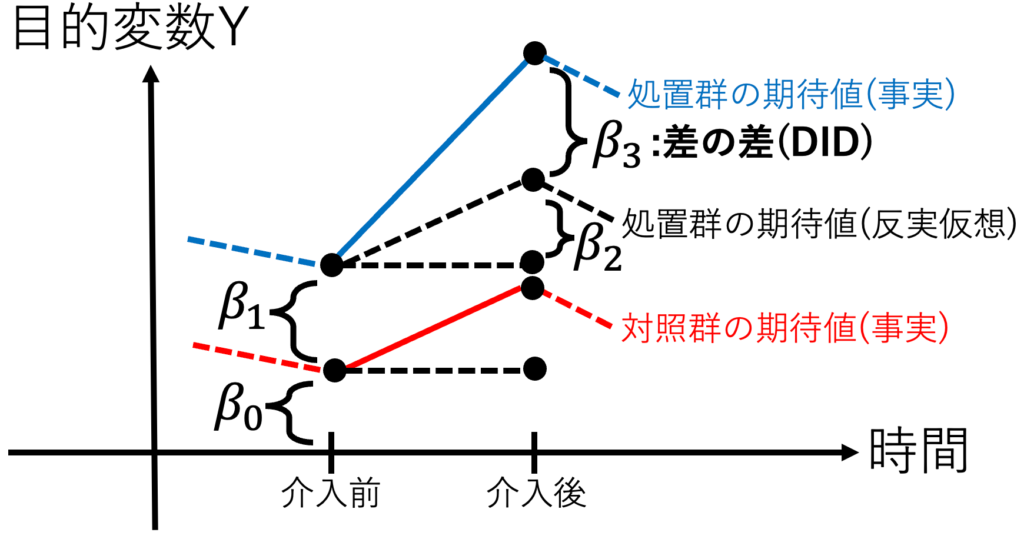
出典:しまうま総研が作成
・【仮定】重回帰モデルの仮定1〜4(定式化、無作為抽出、完全な共線性、外生性)が満たされる。
・【仮定】共通トレンドがある。
第2節:パラメーター
・【因果推論的な解釈】差の差(DID)のβ3が処置群の平均処置効果。
$$処置群の平均処置効果=\beta_3$$
第3節:推定量
・【推定量】最小二乗法(OLS)について / 推定
・【標準誤差】HAC標準誤差を用いるべき。
第4節:実践
#Rコード:差の差分析(クラスター構造に頑健な標準誤差を使用)
library(estimatr)
DID <- lm_robust(y ~ 処置ダミー + 介入後ダミー +介入後ダミー*処置ダミー,
clusters = クラスター変数名, se_type = "stata",
data = Data)
summary(DID)第9章:操作変数法
第1節:モデル
・【全体像】操作変数モデルについて / 内生性への対処
・【注目指標】操作変数で推定した標本回帰係数
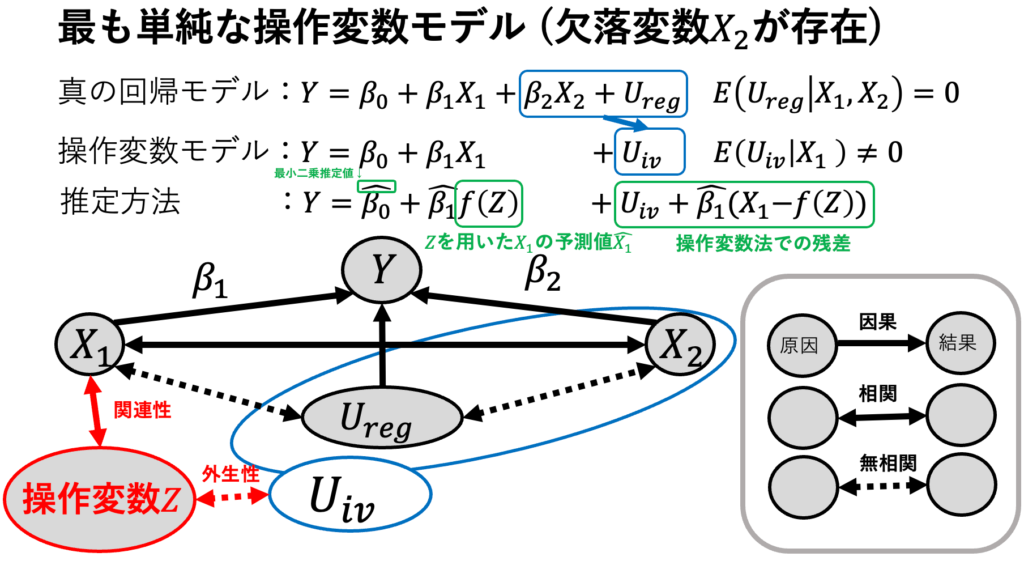
・【仮定】操作変数Zが関連性と外生性を満たす。
第2節:パラメーター
・
第3節:推定量
・2SLS推定量について / 操作変数法(推定量:2段階最小二乗法について)
第4節:実践
#Rコード:操作変数法
library(AER)
ivreg(data = Data, Y ~ X1 + X2 +W1 + W2 | Z1 + Z1 + W1 + W2) #Xは誤差項と相関する内生変数の説明変数、Wは誤差項と相関しない外生変数の説明変数、操作変数はZ第10章:固定効果法
第1節:モデル
第2節:パラメーター
・準備中
第3節:推定量
・【推定量】最小二乗法(OLS)について / 推定
・固定効果推定量について / パネルデータ分析による内生性への対応
第4節:実践
#Rコード:固定効果法
library(plm)
新データフレーム名 <- pdata.frame(元データフレーム名, index = c("グループ名","個体名"))
FE <- plm(formula = Y ~ X1 + X2, model="within", data=新データフレーム名)
summary(FE)第11章:回帰不連続デザイン
第1節:モデル
・回帰不連続デザインについて / LATEの推定(モデル:閾値近傍で擬似的な実験が発生していると解釈するモデル)
$$Y=\beta_{e} D_{介入有ダミー} +f(X)$$
$$局所的な平均処置効果=\beta_e$$
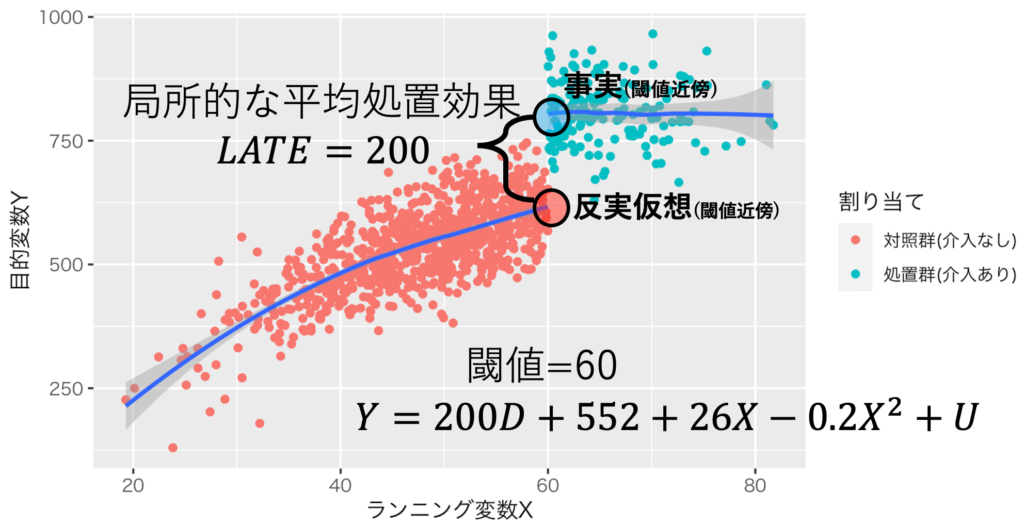
出典:しまうま総研が作成
第2節:パラメーター
・
$$局所的な平均処置効果=\beta_e$$
第3節:推定量
・【推定量】最小二乗法(OLS)について / 推定
第4節:実践
#Rコード
library(rdrobust)
RD <- rdrobust(目的変数,ランニング変数,c = カットオフ値)
summary(RD)第12章:サンプル・セレクション分析
第1節:モデル
・ヘキット・モデルについて / サンプル・セレクション・バイアスの除去
第2節:パラメーター
・準備中
第3節:推定量
・【推定量】最小二乗法(OLS)について / 推定
・【推定量】最尤法について / 推定
・準備中
第4節:実践
#Rコード
library(sampleSelection)
SS <- heckit(s ~ x + z, #セレクション式
y ~ x, #構造式
method = "2step", #2段階推定。"mls"だと最尤法で推定できる
data = Data)
summary(SS)